question_answer

A network of resistors is connected to a 16 V battery of internal resistance of \[1\,\Omega \] as shown in the figure.

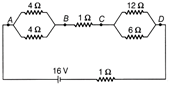
(i) Compute the equivalent resistance of the network.

(ii) Obtain the voltage drops \[{{V}_{AB}}\] and \[{{V}_{CD}}.\]

Answer:

(i) \[4\Omega \] and \[4\Omega \] are in parallel combination. \[\therefore \] Equivalent resistance, \[{{R}_{AB}}=\frac{4}{2}=2\Omega \] Similarly, equivalent resistor of \[12\,\Omega \] and \[6\,\Omega \] resistor \[\frac{1}{{{R}_{CD}}}=\frac{1}{12}+\frac{1}{6}\Rightarrow \frac{1}{{{R}_{CD}}}=\frac{1+2}{12}\Rightarrow {{R}_{CD}}=4\Omega \] Now, the circuit can be redrawn as 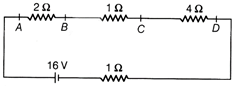Now, \[2\,\Omega ,4\,\Omega \] and \[1\,\Omega ,1\,\Omega \] are in series combination. \[\therefore \] Equivalent resistance of the network             \[{{R}_{eq}}=2\,\Omega +1\Omega +4\Omega +1\Omega =8\Omega \] (ii) Current drawn from the battery             \[I=\frac{V}{R}=\frac{16}{8}=2A\] This current will flow from A to B and C to D. So, the potential difference in between AB and CD can be calculated as Now,     \[{{V}_{AB}}=I{{R}_{AB}}=2\times 2=4V\] and       \[{{V}_{CD}}=I{{R}_{CD}}=2\times 4=8V\]