question_answer

A 1 m long conducting rod rotates with an angular frequency of 400 rad \[{{s}^{-1}}\] about an axis normal to the rod passing through its one end.

The other end of the rod is in contact with a circular metallic ring. A constant magnetic field of 0.5 T parallel to the axis exists everywhere,

Find an expression for the emf induced between the centre and the ring and then calculate the value of induced emf from the given data,

Or

A circuit containing a 80 m H inductor and a \[60\,\mu F\] capacitor in series is connected to a 230 V 50 Hz supply. The resistance of the circuit is negligible.

(i) Obtain the current amplitude and rms values.

(ii) Obtain the rms values of potential drops across each element.

(iii) What is the average power transferred to the inductor?

(iv) What is the average power transferred to the capacitor?

(v) What is the average power absorbed by the circuit?

Answer:

Emf induced between the centre and the ring \[e=\frac{d\phi }{dt}=\frac{d(BA)}{dt}\]             \[[\because \phi =BA]\]             \[e=B\times \frac{dA}{dt}\]                                ?(i) Let the rod subtends an angle, \[\theta \] at centre in time t, then area covered by it 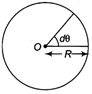\[A=\frac{1}{2}{{R}^{2}}\theta \] \[\therefore \frac{dA}{dt}=\frac{1}{2}{{R}^{2}}\frac{d\theta }{dt}\Rightarrow \frac{dA}{dt}=\frac{1}{2}{{R}^{2}}\omega \] where, \[\omega =d\theta /dt\] is the angular velocity. \[\therefore \] Emf induced, \[e=\frac{1}{2}{{R}^{2}}\omega B\] Given, angular frequency, \[\omega =400\,\,rad\,{{s}^{-1}}\] Magnetic field, B = 0.5 T Length of wire, R = L = 1 m Induced emf, \[e=(1/2)\times {{(1)}^{2}}\times 400\times 0.5=100\,V\] Or Given, inductance of inductor, \[L=80\,mH=80\times {{10}^{-3}}H\] Capacitance of capacitor,             \[C=60\mu F={{6010}^{-6}}F\] Voltage, V = 230 V, Frequency, v = 50 Hz Impedance of the circuit, \[Z=\left( L\omega -\frac{1}{C\omega } \right)\] or \[Z=\left| L\omega -\frac{1}{C\omega } \right|\] \[=\left| \left( 2\pi \times 50\times 8\times {{10}^{-3}}-\frac{1}{2\pi \times 50\times 60\times {{10}^{-6}}} \right) \right|\] \[=\left| (25.12-53.08) \right|=27.93\,\Omega \] (i) Current, \[{{I}_{rms}}=\frac{V}{Z}=\frac{230}{27.96}A=8.23A\] Current amplitude, \[{{I}_{0}}={{I}_{rms}}\sqrt{2}=8.23\times 1.414A=11.63\,A\] (ii) Potential drop across inductor, \[{{V}_{L}}=I{{X}_{L}}=I\omega L=8.23\times 25.12=206.7\,V\] Potential drop across capacitor, \[{{V}_{C}}=I{{X}_{C}}=I\times \frac{1}{\omega C}=8.23\times 53.08=436.8\,V\] (iii) Average power transferred to the inductor, \[\overline{P}={{V}_{L}}{{I}_{L}}\cos 90{}^\circ =0\] (iv) Average power transferred to the capacitor, \[\overline{P}={{V}_{C}}{{I}_{C}}\cos 90{}^\circ =0\] (v) Total average power absorbed by the circuit is zero.