| (i) what will be the forward current at a forward voltage of 0.6V? |
| (ii) what will be the increase in the current, if the voltage across the diode is increased to 0.7V? |
| (iii) what is the dynamic resistance? |
| (iv) what will be the change in current, if reverse bias voltage changes from 1V to 2V? |
| Or |
| (i) Give some practical application of LED. Explain, why the semiconductor used for fabrication of visible light LEDs must have a band gap of at least (nearly) 1.8 eV |
| (ii) Draw a circuit diagram and show the biasing of a light emitting diode (LED). Give its two advantages over conventional incandescent lamps. |
| (iii) Draw energy band diagram of n-type and p-type semiconductor. |
Answer:
In a \[p-n\] junction diode, the expression for current is given as, \[I={{I}_{0}}\exp \left( \frac{eV}{2{{k}_{B}}T}-1 \right)\] where, \[{{I}_{0}}\] = reverse saturation current \[=5\times {{10}^{-12}}A\] T = absolute temperature = 300 K and \[{{k}_{B}}\] = Boltzmann constant \[=8.6\times {{10}^{-5}}eV/K=1.376\times {{10}^{-23}}J{{K}^{-1}}\] V = voltage across the diode (i) Forward voltage, V = 0.6 V \[\therefore \] Current, \[I=5\times {{10}^{-12}}\left[ \exp \left( \frac{1.6\times {{10}^{-19}}\times 0.6}{1.376\times {{10}^{-23}}\times 300}-1 \right) \right]\]\[=5\times {{10}^{-12}}\times [\exp (23.26)-1]=0.063\,A\] Therefore, the forward current is about 0.063 A. (ii) For forward voltage, V = 0.7V, we can write \[I=5\times {{10}^{-12}}\left[ \exp \left( \frac{1.6\times {{10}^{-19}}\times 0.7}{1.376\times {{10}^{-23}}\times 300}-1 \right) \right]\] \[=5\times {{10}^{-12}}\times [\exp (27.14)-1]\] = 3.035 A Hence, the increases in current, \[\Delta I=I'-I\] \[=3.035-0.063=2.972\text{ }A\] (iii) Dynamic resistance \[\text{=}\frac{\text{Change}\,\,\text{in}\,\,\text{voltage}}{\text{Change}\,\,\text{in}\,\,\text{current}}\] \[=\frac{0.7-0.6}{2.976}=\frac{0.1}{2.972}\] \[=0.0336\,\Omega \] (iv) If the reverse bias voltage changes from 1 V to 2V, then the current (I) will almost remain equal to \[{{I}_{0}}\] in both cases. Therefore, the dynamic resistance in the reverse bias will be infinite. Or (i) LEDs emitting visible light are being increasingly used as lighting devices. Infrared LEDs find extensive use in remote controls, burglar alarm systems and optical communication. Spectral range of visible light extends from 400 nm to 700 nm. In other words, energy of visible light photon extends from 1.8 eV (for red light of wavelength 700 nm) to about 3 eV (for violet light of wavelength 400 nm). Therefore, for fabrication of visible light LEDs, the semiconductor used must have a band gap of at least 1.8 eV or more. (ii) The biasing of a light emitting diode (LED) has been shown in figure. A LED is used in forward bias arrangement only. Main advantages of LED over conventional in candescent lamps are as follows (a) The operating voltage is low, power consumption is less and no warm up time is required. (b) The light emitted is nearly monochromatic. The bandwidth of emitted light is \[100\overset{{}^\circ }{\mathop{A}}\,\] to \[500\overset{{}^\circ }{\mathop{A}}\,.\] (c) It is rugged, has a long life and shows fast on-off switching capability. 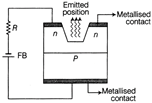 (iii) Energy band diagram for n-type semiconductor
(iii) Energy band diagram for n-type semiconductor 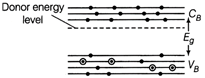 Energy hand diagram for p-type semiconductor
Energy hand diagram for p-type semiconductor 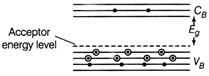
You need to login to perform this action.
You will be redirected in
3 sec
