Answer:
According to the lens maker formula, \[\frac{1}{f}=(\mu -1)\left[ \frac{1}{{{R}_{1}}}-\frac{1}{{{R}_{2}}} \right]\] For plano-convex lens, \[{{R}_{1}}=R\] and \[{{R}_{2}}=\infty ,\] \[\mu =1.5\] (given) \[\therefore \] \[\frac{1}{f}=(\mu -1)\left[ \frac{1}{R}-\frac{1}{\infty } \right]\Rightarrow f=\frac{R}{(\mu -1)}\] \[f=2R\,\,\left( \text{putting},\mu =\frac{3}{2} \right)\] ?(i) It r is the radius and y is the thickness of the lens (at the centre), we have from the figure, \[{{R}^{2}}={{r}^{2}}+{{(R-Y)}^{2}}\] \[\therefore \] \[R=\frac{{{r}^{2}}+{{y}^{2}}}{2y}\]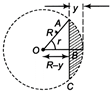 
Since, \[r=\frac{6}{2}=3cm,\] y = 4 mm \[\therefore \] \[R\simeq \frac{{{r}^{2}}}{2y}\] \[({{r}^{2}}+{{y}^{2}}\approx {{r}^{2}},\because r>y)\] \[=\frac{9}{2\times 4\times {{10}^{-1}}}=1125\,cm\] Putting the value of fi into Eq. (i), we get \[f=2\times R=2\times 11.25\] \[(\therefore f=22.5\,cm)\]
You need to login to perform this action.
You will be redirected in
3 sec
