A) \[\frac{mg{{R}^{2}}}{l}\]
B) \[\frac{mg{{R}^{2}}}{l}\sin \left( \frac{l}{R} \right)\]
C) \[\frac{mg{{R}^{2}}}{l}\cos \left( \frac{l}{R} \right)\]
D) None of these
Correct Answer: B
Solution :
| [b] \[\sin \alpha =\frac{l}{R}\] |
| Consider the element of the chain as shown in the figure below. Its mass is \[dm=\frac{m}{l}\times Rd\theta \] |
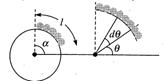 |
| Its\[PE\,wrt\]horizontal diagram as the reference position is |
| \[dU=dmg\times R\sin \theta \] |
| \[dU=\frac{m{{R}^{2}}2}{l}\sin \theta \,d\theta \] |
| \[U=\int_{{}}^{{}}{dU=\int_{\pi /2-\alpha }^{\pi /2}{\frac{m{{R}^{2}}g}{l}}\sin \theta d\theta }\] |
| \[=\frac{m{{R}^{2}}g}{l}\sin \alpha =\frac{m{{R}^{2}}g}{l}\sin \left( \frac{l}{R} \right)\] |
You need to login to perform this action.
You will be redirected in
3 sec
