question_answer

Two identical balls A and B are released from the positions shown in figure. They collide elastically on horizontal portion\[M/N\]. All surfaces are smooth. The ratio of heights attained by A and B after collision will be  

A) \[1:4\]

B) \[2:1\]                           

C) \[4:13\]

D) \[2:5\]

Correct Answer: C

Solution :

[c] After collision, balls exchange their velocities

\[\therefore \] \[{{V}_{A}}=\sqrt{2gh}\]  and  \[{{V}_{B}}=\sqrt{2g(4h)}=2\sqrt{2gh}\]

Height gained by A will be  \[{{h}_{A}}=h\]

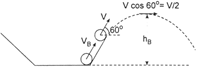But path of B will be first straight line and then parabolic as shown in figure

After calculation, we can show that \[{{h}_{B}}=\frac{13}{4}h\]

\[\therefore \]      \[\frac{{{h}_{A}}}{{{h}_{B}}}=\frac{4}{13}\]