A) 30, 60
B) 60, 30
C) 40, 60
D) 60, 40
Correct Answer: B
Solution :
The given data may be put in the following tobular form| Refinery | High grade | Medium grade | Low grade | Cost per day |
| A | 100 | 300 | 200 | Rs 400 |
| B | 200 | 400 | 100 | Rs 300 |
| Minimum requirement | 12000 | 20000 | 15000 |
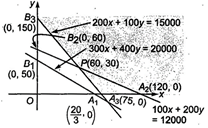
| Point \[(x,y)\] | \[Z=400x+300y\] |
| \[{{A}_{2}}(120,0)\] | 48000 |
| \[P(60,30)\] | 33000 |
| \[{{B}_{3}}(0,150)\] | 45000 |
You need to login to perform this action.
You will be redirected in
3 sec
