question_answer 1) The height y and distance x along the horizontal plane of projectile on a certain planet (with no surrounding) are given by: \[y=(8t-5{{t}^{2}})\] metre and x = 6t metre where t is in second. The velocity with which the projectile is projected is:
A)
8 m/s
done
clear
B)
6 m/s
done
clear
C)
10 m/s
done
clear
D)
data is not sufficient
done
clear
View Answer play_arrow
question_answer 2) A body of mass a, moving with a velocity b collides with a body of mass c, at rest and sticks to it. They move together with a velocity given by:
A)
\[\frac{ac}{a+b}\]
done
clear
B)
\[\frac{ab}{a+c}\]
done
clear
C)
\[\frac{a+b}{ac}\]
done
clear
D)
\[\frac{b+c}{ab}\]
done
clear
View Answer play_arrow
question_answer 3) The refractive index of a material is given by the equation \[n=\frac{A+B}{{{\lambda }^{2}}},\] where A and B are constants. The dimensional formula for B is:
A)
\[\text{ }\!\![\!\!\text{ }{{\text{M}}^{\text{0}}}{{\text{L}}^{\text{2}}}{{\text{T}}^{\text{-1}}}\text{ }\!\!]\!\!\text{ }\]
done
clear
B)
\[\text{ }\!\![\!\!\text{ }{{\text{M}}^{\text{0}}}{{\text{L}}^{-2}}{{\text{T}}^{0}}\text{ }\!\!]\!\!\text{ }\]
done
clear
C)
\[\text{ }\!\![\!\!\text{ }{{\text{M}}^{\text{0}}}{{\text{L}}^{2}}{{\text{T}}^{-2}}\text{ }\!\!]\!\!\text{ }\]
done
clear
D)
\[\text{ }\!\![\!\!\text{ }{{\text{M}}^{\text{0}}}{{\text{L}}^{2}}{{\text{T}}^{0}}\text{ }\!\!]\!\!\text{ }\]
done
clear
View Answer play_arrow
question_answer 4) A satellite is orbiting around the earth. By what percentage should we increase its velocity, so as to enable it escape away from the earth?
A)
41.4%
done
clear
B)
50%
done
clear
C)
82.8%
done
clear
D)
100%
done
clear
View Answer play_arrow
question_answer 5) At what temperature, the hydrogen molecule will escape from earths surface?
A)
\[{{10}^{1}}K\]
done
clear
B)
\[{{10}^{2}}K\]
done
clear
C)
\[{{10}^{3}}K\]
done
clear
D)
\[{{10}^{4}}K\]
done
clear
View Answer play_arrow
question_answer 6) If the earth is at one-fourth of its present distance from the sun, the duration of the year will be:
A)
half the present year
done
clear
B)
one-eighth the present year
done
clear
C)
one-fourth the present year
done
clear
D)
one-sixth the present year
done
clear
View Answer play_arrow
question_answer 7) An observer moves towards a stationary source of sound with a velocity one-tenth the velocity of sound. The apparent increase in frequency is:
A)
zero
done
clear
B)
10%
done
clear
C)
5%
done
clear
D)
0.1%
done
clear
View Answer play_arrow
question_answer 8) When two conductors of charges and potentials \[{{C}_{1}},\,{{V}_{1}}\] and \[{{C}_{2}},\,{{V}_{2}}\] respectively are joined, the common potential will be:
A)
\[\frac{{{V}_{1}}{{V}_{1}}+{{C}_{2}}{{V}_{2}}}{{{V}_{1}}+{{V}_{2}}}\]
done
clear
B)
\[\frac{{{C}_{1}}{{V}_{1}}^{2}+{{C}_{2}}{{V}_{2}}^{2}}{{{V}_{1}}^{2}+{{V}_{2}}^{2}}\]
done
clear
C)
\[{{C}_{1}}+{{C}_{2}}\]
done
clear
D)
\[\frac{{{C}_{1}}{{V}_{1}}+{{C}_{2}}{{V}_{2}}^{2}}{{{C}_{1}}+{{C}_{2}}}\]
done
clear
View Answer play_arrow
question_answer 9) A weightless thread can bear tension upto 3.7 kg-wt. A stone of mass 500 g is tied to it and revolved in a circular path of radius 4 m in a vertical plane. If \[g=10\,m/{{s}^{-2}},\] then the maximum angular velocity of the stone will be:
A)
4 rad/s
done
clear
B)
16 rad/s
done
clear
C)
\[\sqrt{21}\]rad/s
done
clear
D)
2 rad/s
done
clear
View Answer play_arrow
question_answer 10) The effective length of a magnet is 31.4 cm and its pole strength is 0.5 Am. If it is bent in the form of semicircle, what will be its magnetic moment then?
A)
\[0.12\,A{{m}^{2}}\]
done
clear
B)
\[0.1\,A{{m}^{2}}\]
done
clear
C)
\[0.05\,A{{m}^{2}}\]
done
clear
D)
\[0.01\,A{{m}^{2}}\]
done
clear
View Answer play_arrow
question_answer 11) Four molecules of a gas have speeds 1, 2, 3 and \[4\,km{{s}^{-1}}\]. The value of ms speed of the gas molecules is:
A)
\[\frac{\text{1}}{\text{2}}\sqrt{\text{15}}\text{km}{{\text{s}}^{\text{-1}}}\]
done
clear
B)
\[\frac{\text{1}}{\text{2}}\sqrt{\text{10}}\text{km}{{\text{s}}^{\text{-1}}}\]
done
clear
C)
\[\text{2}\text{.5km}{{\text{s}}^{\text{-1}}}\]
done
clear
D)
\[\sqrt{\frac{15}{2}}\text{km}{{\text{s}}^{\text{-1}}}\]
done
clear
View Answer play_arrow
question_answer 12) If there is change of angular momentum from J to 5 J in 5 s, then the torque is:
A)
\[\frac{\text{3J}}{\text{5}}\]
done
clear
B)
\[\frac{\text{4J}}{\text{5}}\]
done
clear
C)
\[\frac{\text{5J}}{4}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
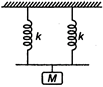
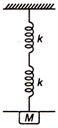
question_answer 13) Two springs having force constants k each are arranged in parallel and in series. A mass M is attached to two arrangements separately. If time period in first case is \[{{T}_{1}}\] and in second case is \[{{T}_{2}}\] then ratio \[\frac{{{T}_{1}}}{{{T}_{2}}}\] is:
A)
1.5
done
clear
B)
3.2
done
clear
C)
0.5
done
clear
D)
2.1
done
clear
View Answer play_arrow
question_answer 14) If the work done in blowing a bubble of volume V is W, then the work done in blowing a soap bubble of volume 2V will be:
A)
W
done
clear
B)
2 W
done
clear
C)
\[\sqrt{2}\]W
done
clear
D)
\[{{4}^{1/3}}W\]
done
clear
View Answer play_arrow
question_answer 15)
An ideal monoatomic gas is taken round the cycle ABCDA as shown in figure. The work done during the cycle is :
A)
\[PV\]
done
clear
B)
\[2PV\]
done
clear
C)
\[\frac{PV}{2}\]
done
clear
D)
\[\text{zero}\]
done
clear
View Answer play_arrow
question_answer 16) A proton of energy 2 MeV is moving in a circular path in a magnetic field. What should be the energy of a deuteron, so that it also describes circular path of radius equal to that of the proton?
A)
1 MeV
done
clear
B)
2 MeV
done
clear
C)
4 MeV
done
clear
D)
0.5 MeV
done
clear
View Answer play_arrow
question_answer 17) A gas at NTP is suddenly compressed to one-fourth of its original volume. If \[\gamma \] is supposed to be 3/2, then the final pressure is:
A)
4 atm
done
clear
B)
\[\frac{3}{2}\] atm
done
clear
C)
8 atm
done
clear
D)
\[\frac{1}{4}\] atm
done
clear
View Answer play_arrow
question_answer 18) In a series combination\[R=300\,\Omega ,\]\[\text{L=0}\text{.9H,}\]\[\text{C=2}\text{.0}\,\text{F,}\]\[\omega =1000\,\text{rad/s,}\]the impedance of the circuit is :
A)
1300\[\Omega \]
done
clear
B)
900\[\Omega \]
done
clear
C)
500\[\Omega \]
done
clear
D)
400\[\Omega \]
done
clear
View Answer play_arrow
question_answer 19) n identical spherical drops each of radius r are charged to same potential V. They combine to form a bigger drop. The potential of the big drop will be:
A)
\[{{n}^{1/3}}V\]
done
clear
B)
\[{{n}^{2/3}}V\]
done
clear
C)
V
done
clear
D)
\[nV\]
done
clear
View Answer play_arrow
question_answer 20) The wavelength of maximum energy, released during an atomic explosion was \[2.93\,\times {{10}^{-10}}\,m\]. Given that the Wiens constant is \[2.93\,\times {{10}^{-10}}m-K,\] the maximum temperature attained must be of the order of:
A)
\[{{10}^{-7}}K\]
done
clear
B)
\[{{10}^{7}}K\]
done
clear
C)
\[{{10}^{-3}}K\]
done
clear
D)
\[5.86\,\times {{10}^{7}}K\]
done
clear
View Answer play_arrow
question_answer 21) The pressure and density of a diatomic gas \[\left( \gamma =\frac{7}{5} \right)\]change adiabatically from (P, d) to (P, d). If \[\frac{d}{d}=32,\] then\[\frac{P}{P}\] should be:
A)
\[\frac{1}{128}\]
done
clear
B)
32
done
clear
C)
128
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 22) A piece of wax weighs 18.03 g in air. A piece of metal is found to weigh 17.03 g in water. It is tied to the wax and both together weigh 15.23 g in water. Then, the specific gravity of wax is:
A)
\[\frac{18.03}{17.03}\]
done
clear
B)
\[\frac{17.03}{18.03}\]
done
clear
C)
\[\frac{18.03}{19.83}\]
done
clear
D)
\[\frac{15.03}{17.83}\]
done
clear
View Answer play_arrow
question_answer 23) If a mica sheet of thickness t and refractive index \[\mu \] is placed in the path of one of interfering beams in a double slit experiment, then displacement of fringes will be:
A)
\[\frac{D}{d}\mu t\]
done
clear
B)
\[\frac{D}{d}(\mu -1)t\]
done
clear
C)
\[\frac{D}{d}(\mu +1)t\]
done
clear
D)
\[\frac{D}{d}({{\mu }^{2}}-1)t\]
done
clear
View Answer play_arrow
question_answer 24) A ray of light propagates from glass (refractive index\[=\frac{3}{2})\] to water (refractive index\[=\frac{4}{3}).\] The value of the critical angle is:
A)
\[{{\sin }^{-1}}\left( \frac{1}{2} \right)\]
done
clear
B)
\[{{\sin }^{-1}}\left( \sqrt{\frac{9}{8}} \right)\]
done
clear
C)
\[{{\sin }^{-1}}\left( \frac{8}{9} \right)\]
done
clear
D)
\[{{\sin }^{-1}}\left( \frac{5}{7} \right)\]
done
clear
View Answer play_arrow
question_answer 25) A ray of light suffers minimum deviation when incident at 60° prism of refractive index \[\sqrt{2.}\] The angle of incidence is:
A)
\[{{\sin }^{-1}}(0.8)\]
done
clear
B)
\[60{}^\circ \]
done
clear
C)
\[45{}^\circ \]
done
clear
D)
\[30{}^\circ \]
done
clear
View Answer play_arrow
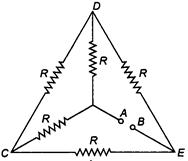
question_answer 26) Each of the resistance in the network shown in figure is equal to R. Find the equivalent resistance between two terminals A and B.
A)
\[R\]
done
clear
B)
\[5R\]
done
clear
C)
\[2R\]
done
clear
D)
\[\frac{2}{3}R\]
done
clear
View Answer play_arrow
question_answer 27) A gas in an air tight container is heated from \[25{}^\circ C\] to \[90{}^\circ C\]. The density of gas will:
A)
increase slightly
done
clear
B)
remain the same
done
clear
C)
increase considerably
done
clear
D)
decrease slightly
done
clear
View Answer play_arrow
question_answer 28) If 2% of the main current is to be passed through the galvanometer of resistance G, the resistance of the shunt required is:
A)
\[\frac{G}{49}\]
done
clear
B)
\[\frac{G}{50}\]
done
clear
C)
49 G
done
clear
D)
50 G
done
clear
View Answer play_arrow
question_answer 29) The current in self-inductance L = 40 mH is increased uniformly from 1 A to 11 A in 4 milliseconds. The induced emf produced in L during this process will be:
A)
100 V
done
clear
B)
0.2V
done
clear
C)
440 V
done
clear
D)
40 V
done
clear
View Answer play_arrow
question_answer 30) \[{{\text{H}}^{\text{+}}}\]\[\text{H}{{\text{e}}^{2+}}\] and \[{{\text{O}}^{\text{2-}}}\] all having the same kinetic energy pass through a region in which there is a uniform magnetic field perpendicular to their velocity. The masses of \[{{\text{H}}^{\text{+}}}\text{,}\] \[\text{H}{{\text{e}}^{\text{2+}}}\] and \[{{\text{O}}^{\text{2-}}}\] are 1 amu, 4 amu and 16 amu, respectively. Then:
A)
\[{{\text{H}}^{\text{+}}}\] will be deflected most
done
clear
B)
\[{{\text{O}}^{\text{2}}}\] will be deflected most
done
clear
C)
\[H{{e}^{\text{2+}}}\]and \[{{\text{O}}^{\text{2-}}}\] will be deflected most
done
clear
D)
all will be deflected most
done
clear
View Answer play_arrow
question_answer 31) The current gain of a transistor in common emitter mode is 49. The change in collector current and emitter current corresponding to the change in base current by \[5.0\,\mu A\] are:
A)
\[\Delta iC=245\,\mu A,\]\[\Delta {{i}_{E}}=250\,\mu A\]
done
clear
B)
\[\Delta {{i}_{C}}=252\,\mu A,\,\]\[\,\Delta {{i}_{E}}=145\mu A\]
done
clear
C)
\[\Delta {{i}_{C}}=125\,\mu A,\,\]\[\Delta {{i}_{E}}=250\mu A\]
done
clear
D)
\[\Delta {{i}_{C}}=252\,\mu A,\]\[\Delta {{i}_{E}}=230\mu A\]
done
clear
View Answer play_arrow
question_answer 32) In hydrogen atom when an electron jumps from second to first orbit, the wavelength of line emitted is :
A)
\[0.563\,\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
B)
\[4861\,\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
C)
\[4102\,\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
D)
\[1213\,\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
View Answer play_arrow
question_answer 33) How does the magnetic susceptibility \[\chi \] of a paramagnetic material change with absolute temperature T?
A)
\[\chi \propto T\]
done
clear
B)
\[\chi \propto {{T}^{-1}}\]
done
clear
C)
\[\chi =\] constant
done
clear
D)
\[\chi \propto {{e}^{T}}\]
done
clear
View Answer play_arrow
question_answer 34) Two identical heaters of 220 V, 1000 W are placed in parallel with each other across 220 V line, then the combined power is:
A)
1000 W
done
clear
B)
2000 W
done
clear
C)
500 W
done
clear
D)
4000 W
done
clear
View Answer play_arrow
question_answer 35) A bar of magnetic moment M is cut into two pans of equal length. The magnetic moment of either part is;
A)
\[M\]
done
clear
B)
\[2M\]
done
clear
C)
\[\frac{M}{2}\]
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 36) A rain drop of radius 0.3 mm has a terminal velocity of 1 m/s and the viscosity of 1 m/s and the viscosity of air is \[18\times {{10}^{-5}}\] poise. The viscous force on the drop is:
A)
\[16.95\times {{10}^{-9}}\,N\]
done
clear
B)
\[1.695\times {{10}^{-9}}\,N\]
done
clear
C)
\[10.17\times {{10}^{-9}}\,N\]
done
clear
D)
\[101.17\times {{10}^{-9}}\,N\]
done
clear
View Answer play_arrow
question_answer 37) If magnetic material moves from stronger to weaker parts of magnetic field, then it is known as:
A)
anti-ferromagnetic
done
clear
B)
ferromagnetic
done
clear
C)
diamagnetic
done
clear
D)
paramagnetic
done
clear
View Answer play_arrow
question_answer 38) A charge q is placed at the centre of line joining two equal charges Q. The system of three charges will be in equilibrium, if q is equal to:
A)
\[-\frac{Q}{2}\]
done
clear
B)
\[-\frac{Q}{4}\]
done
clear
C)
\[+\frac{Q}{4}\]
done
clear
D)
\[+\frac{Q}{2}\]
done
clear
View Answer play_arrow
question_answer 39) The temperature of cold, hot junction of a thermocouple are \[0{}^\circ C\] and \[T{}^\circ C\] respectively. The thermo-emf produced is\[E=AT-\frac{1}{2}B{{T}^{2}}.\]If A = 16, B = 0.08, the temperature of inversion will be:
A)
\[100{}^\circ C\]
done
clear
B)
\[300{}^\circ C\]
done
clear
C)
\[400{}^\circ C\]
done
clear
D)
\[500{}^\circ C\]
done
clear
View Answer play_arrow
question_answer 40)
Two light springs of force constants \[{{k}_{1}}\] and \[{{k}_{2}}\] and a block of mass m are in one line AS on a smooth horizontal table, such that one end of each spring is fixed to rigid support and other end is attached to block of mass m kg as shown in figure. The frequency of vibration is:
A)
\[n=\frac{1}{2\pi }\sqrt{\frac{{{k}_{1}}+{{k}_{2}}}{m}}\]
done
clear
B)
\[n=\frac{1}{2\pi }\sqrt{\frac{{{k}_{1}}{{k}_{2}}}{m}}\]
done
clear
C)
\[n=\frac{1}{2\pi }\sqrt{\frac{{{k}_{1}}-{{k}_{2}}}{m}}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 41) Pressure inside two soap bubbles are 1.01 and 1.02 atm. Ratio between their volumes is:
A)
102 : 101
done
clear
B)
\[{{(102)}^{3}}:{{(103)}^{3}}\]
done
clear
C)
8 : 1
done
clear
D)
2 : 1
done
clear
View Answer play_arrow
question_answer 42)
Two dielectrics of dielectric constants \[{{K}_{1}}\] and \[{{K}_{2}}\]are filled in gap of parallel plate capacitor as shown in figure
A)
\[\frac{{{\varepsilon }_{0}}A({{K}_{1}}+{{K}_{2}})}{2d}\]
done
clear
B)
\[\frac{{{\varepsilon }_{0}}A}{2d}\left( \frac{{{K}_{1}}+{{K}_{2}}}{{{K}_{1}}{{K}_{2}}} \right)\]
done
clear
C)
\[\frac{{{\varepsilon }_{0}}}{d}\left( \frac{{{K}_{1}}{{K}_{2}}}{{{K}_{1}}+{{K}_{2}}} \right)\]
done
clear
D)
\[\frac{{{\varepsilon }_{0}}A}{d}\left( \frac{{{K}_{1}}+{{K}_{2}}}{{{K}_{1}}{{K}_{2}}} \right)\]
done
clear
View Answer play_arrow
question_answer 43) For a series LCR circuit, the phase difference between current and voltage at the condition of resonance will be:
A)
\[\frac{\pi }{2}\]
done
clear
B)
\[\frac{\pi }{4}\]
done
clear
C)
zero
done
clear
D)
nothing can be said
done
clear
View Answer play_arrow
question_answer 44) A metallic rod of length \[l\] is placed normal to the magnetic field B and revolved in a circular path about one of the ends with angular frequency m. The potential difference across the ends will be:
A)
\[\frac{1}{2}{{B}^{2}}l\omega \]
done
clear
B)
\[\frac{1}{2}B\omega {{l}^{2}}\]
done
clear
C)
\[\frac{1}{8}B\omega {{l}^{3}}\]
done
clear
D)
\[B\omega {{l}^{3}}\]
done
clear
View Answer play_arrow
question_answer 45) A magnetic needle suspended in a vertical plane at \[30{}^\circ \] from the magnetic meridian makes an angle \[45{}^\circ \] with the horizontal. What will be the true angle of dip?
A)
\[{{\tan }^{-1}}\left( \frac{\sqrt{3}}{2} \right)\]
done
clear
B)
\[{{\tan }^{-1}}(\sqrt{3})\]
done
clear
C)
\[{{45}^{0}}\]
done
clear
D)
\[{{30}^{0}}\]
done
clear
View Answer play_arrow
question_answer 46) A force F is given by \[f=at+b{{t}^{2}},\] where t is rime. What are the dimensions of a and b respectively?
A)
\[\text{ }\!\![\!\!\text{ ML}{{\text{T}}^{\text{-1}}}\text{ }\!\!]\!\!\text{ and}\,\text{ }\!\![\!\!\text{ ML}{{\text{T}}^{\text{-4}}}\text{ }\!\!]\!\!\text{ }\]
done
clear
B)
\[\text{ }\!\![\!\!\text{ ML}{{\text{T}}^{\text{-3}}}\text{ }\!\!]\!\!\text{ and}\,\text{ }\!\![\!\!\text{ ML}{{\text{T}}^{\text{-4}}}\text{ }\!\!]\!\!\text{ }\]
done
clear
C)
\[\text{ }\!\![\!\!\text{ ML}{{\text{T}}^{\text{-4}}}\text{ }\!\!]\!\!\text{ and}\,\text{ }\!\![\!\!\text{ ML}{{\text{T}}^{\text{-2}}}\text{ }\!\!]\!\!\text{ }\]
done
clear
D)
\[\text{ }\!\![\!\!\text{ M}{{\text{L}}^{2}}{{\text{T}}^{3}}\text{ }\!\!]\!\!\text{ and}\,\text{ }\!\![\!\!\text{ }{{\text{M}}^{-1}}{{\text{L}}^{2}}\text{T }\!\!]\!\!\text{ }\]
done
clear
View Answer play_arrow
question_answer 47) In a triode valve, the plate resistance is 10000\[\Omega \] and the anode load resistance is 30000\[\Omega \]. If the amplification factor is 36, then the voltage gain is:
A)
9
done
clear
B)
27
done
clear
C)
36
done
clear
D)
108
done
clear
View Answer play_arrow
question_answer 48) \[{{g}_{e}}\] and\[{{g}_{p}}\] denote the acceleration due to gravity on the surface of the earth and another planet whose mass and radius are twice to that of the earth, then:
A)
\[{{g}_{p}}=\frac{{{g}_{e}}}{2}\]
done
clear
B)
\[{{g}_{p}}={{g}_{e}}\]
done
clear
C)
\[{{g}_{p}}=2{{g}_{e}}\]
done
clear
D)
\[{{g}_{p}}=\frac{{{g}_{e}}}{\sqrt{2}}\]
done
clear
View Answer play_arrow
question_answer 49) Of the following which relation is true:
A)
\[\beta >\alpha \]
done
clear
B)
\[\alpha >\beta \]
done
clear
C)
\[\alpha \,\beta =1\]
done
clear
D)
\[\alpha =\beta \]
done
clear
View Answer play_arrow
question_answer 50) A soap bubble in vacuum has a radius 3 cm and another soap bubble in vacuum has radius 4 cm If two bubbles coalesce under isothermal condition, then the radius of the new bubble will be :
A)
7 cm
done
clear
B)
5 cm
done
clear
C)
4.5 cm
done
clear
D)
2.3 cm
done
clear
View Answer play_arrow
question_answer 51) Out of Cu, Al Fe and Zn, metal which can displace all others from their salt solution is:
A)
Al
done
clear
B)
Cu
done
clear
C)
Zn
done
clear
D)
Fe
done
clear
View Answer play_arrow
question_answer 52) In which of the following reactions, hydrogen is acting as an oxidizing agent?
A)
With Li to form \[LiH\]
done
clear
B)
With \[{{I}_{2}}\] to give HI
done
clear
C)
With S to give \[{{H}_{2}}S\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 53) Our cells get energy by the conversion of:
A)
ATP \[\xrightarrow{{}}\] Adenine
done
clear
B)
ATP \[\xrightarrow{{}}\]ADP
done
clear
C)
ADP\[\xrightarrow{{}}\]AMP
done
clear
D)
CDP\[\xrightarrow{{}}\] CTP
done
clear
View Answer play_arrow
question_answer 54) The number of optically active isomers of tartaric acid are:
A)
1
done
clear
B)
3
done
clear
C)
4
done
clear
D)
2
done
clear
View Answer play_arrow
question_answer 55) The hardness of water is estimated by:
A)
conductivity method
done
clear
B)
titrimetric method
done
clear
C)
EDTA method
done
clear
D)
distillation method
done
clear
View Answer play_arrow
question_answer 56) \[N{{a}_{2}}O,\,MgO,\,A{{l}_{2}}{{O}_{3}}\] and \[Si{{O}_{2}}\]have heat of formation equal to \[-416,-602,-1676\] and \[-911\,kJ\,mo{{l}^{-1}}\]respectively. The most stable oxide is:
A)
\[N{{a}_{2}}O\]
done
clear
B)
\[MgO\]
done
clear
C)
\[A{{l}_{2}}{{O}_{3}}\]
done
clear
D)
\[Si{{O}_{2}}\]
done
clear
View Answer play_arrow
question_answer 57) A photon having a wavelength of \[845\text{ }\overset{\text{o}}{\mathop{\text{A}}}\,,\] causes the ionization of N atom. What is the ionization energy of N?
A)
\[1.4\,kJ\]
done
clear
B)
\[1.4\,\times {{10}^{4}}\,kJ\]
done
clear
C)
\[1.4\,\times {{10}^{2}}\,kJ\]
done
clear
D)
\[1.4\,\times {{10}^{3}}\,kJ\]
done
clear
View Answer play_arrow
question_answer 58) The electronic theory of bonding was proposed by:
A)
Pauling
done
clear
B)
Lewis
done
clear
C)
Hronsted
done
clear
D)
Mullikan
done
clear
View Answer play_arrow
question_answer 59) An azeotropic mixture of two liquids has boiling point lower than either of them, when it:
A)
shows a negative deviation from Raoults law
done
clear
B)
shows no deviation from Raoults law
done
clear
C)
shows positive deviation from Raoults law
done
clear
D)
is saturated
done
clear
View Answer play_arrow
question_answer 60) Troutons rule gives the relation between:
A)
\[{{T}_{b}}\] and\[{{T}_{c}}\]
done
clear
B)
\[{{T}_{b}}\] and critical pressure
done
clear
C)
enthalpy of vaporization and boiling point
done
clear
D)
normal boiling point and boiling point
done
clear
View Answer play_arrow
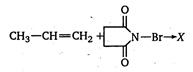
question_answer 61)
The product X, in the following reaction is:
A)
\[C{{H}_{2}}Br-CH=C{{H}_{2}}\]
done
clear
B)
\[C{{H}_{3}}-\overset{Br}{\mathop{\overset{|}{\mathop{C}}\,}}\,=C{{H}_{2}}\]
done
clear
C)
\[C{{H}_{3}}CH=CHBr\]
done
clear
D)
none of the above
done
clear
View Answer play_arrow
question_answer 62) What are the products in the following reaction? \[{{C}_{2}}{{H}_{5}}O{{C}_{2}}{{H}_{5}}\xrightarrow[cold]{HI}X+Y\]
A)
\[C{{H}_{3}}COOH,C{{H}_{2}}=C{{H}_{2}}\]
done
clear
B)
\[C{{H}_{3}}CHO,\,C{{H}_{2}}=C{{H}_{2}}\]
done
clear
C)
\[{{C}_{2}}{{H}_{5}}OH,{{C}_{2}}{{H}_{5}}I\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 63) Which of the following reagent can distinguish between butyne-1 and butyne-2?
A)
Bromine water
done
clear
B)
Aqueous
done
clear
C)
Fehlings solution
done
clear
D)
Ammoniacal\[AgN{{O}_{3}}\]
done
clear
View Answer play_arrow
question_answer 64) Which of the following will have maximum pH?
A)
\[\frac{M}{10}HCl\]
done
clear
B)
\[\frac{M}{100}HCl\]
done
clear
C)
\[\frac{M}{10}NaOH\]
done
clear
D)
\[\frac{M}{100}NaOH\]
done
clear
View Answer play_arrow
question_answer 65) What is AE for system that does 500 cal of work on surrounding and 300 cal of heat is absorbed by the system?
A)
\[-200\]cal
done
clear
B)
\[-300\]cal
done
clear
C)
\[+\,200\]cal
done
clear
D)
\[+\text{ }300\]cal
done
clear
View Answer play_arrow
question_answer 66) The rate of a chemical reaction:
A)
increase as the reaction proceeds
done
clear
B)
decrease as the reaction proceeds
done
clear
C)
may increase or decrease during reaction
done
clear
D)
remain constant as the reaction
done
clear
View Answer play_arrow
question_answer 67) A carbonate ore is:
A)
camallite
done
clear
B)
limonite
done
clear
C)
siderite
done
clear
D)
horn silver
done
clear
View Answer play_arrow
question_answer 68) Cadmium in a nuclear reactor acts as:
A)
nuclear fuel
done
clear
B)
neutron absorber
done
clear
C)
a moderator
done
clear
D)
neutron liberator to start the chain
done
clear
View Answer play_arrow
question_answer 69) Cement does not contain:
A)
calcium
done
clear
B)
aluminium
done
clear
C)
sulphur
done
clear
D)
iron
done
clear
View Answer play_arrow
question_answer 70) The simplest way, to check whether a system is a colloid, is by:
A)
Tyndall effect
done
clear
B)
Brownian movement
done
clear
C)
Electrodialysis
done
clear
D)
finding out particle size
done
clear
View Answer play_arrow
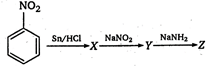
question_answer 71)
What is Z in the following reaction?
A)
Benzoic acid
done
clear
B)
Cyanobenzoic acid
done
clear
C)
Benzamide
done
clear
D)
Aniline
done
clear
View Answer play_arrow
question_answer 72) The reaction, \[RCOOH\xrightarrow{Na{{N}_{3}}/conc.{{H}_{2}}S{{O}_{4}}}\] \[RN{{H}_{2}}+{{N}_{2}}+C{{O}_{2}}\] is known as:
A)
Curtius reaction
done
clear
B)
Lossen reaction
done
clear
C)
Schmidt reaction
done
clear
D)
Hofmann reaction
done
clear
View Answer play_arrow
question_answer 73) What is the product in the reaction? \[C{{H}_{3}}MgBr\xrightarrow[(ii)\,{{H}_{2}}O]{(i)\,C{{O}_{2}}}X\]
A)
Acetaldehyde
done
clear
B)
Acetic acid
done
clear
C)
Formic acid
done
clear
D)
Formaldehyde
done
clear
View Answer play_arrow
question_answer 74) What is the value of \[{{E}_{cell}}\] \[Cr|C{{r}^{3+}}(0.1M)||F{{e}^{2+}}(0.01\,M)|Fe\] Given, \[E_{C{{r}^{3+}}/Cr}^{o}=-0.74\,V\] and \[E_{F{{e}^{2+}}/Fe}^{o}=-0.44\,V\]
A)
\[~+\text{ }0.2941\,V\]
done
clear
B)
\[~+\text{ }0.5212\,V\]
done
clear
C)
\[+\text{ }0.1308\,V\]
done
clear
D)
\[-\,0.2606\,V\]
done
clear
View Answer play_arrow
question_answer 75) Elevation in boiling point was \[0.52{{\,}^{o}}C\]when 6g of a compound was dissolved in 100 g of water. Molecular weight of X is (\[{{K}_{b}}\]of water is \[5.2{{\,}^{o}}C\] per 100 g of water):
A)
120
done
clear
B)
60
done
clear
C)
600
done
clear
D)
180
done
clear
View Answer play_arrow
question_answer 76) The solubility of \[PbC{{l}_{2}}\]is:
A)
\[\sqrt{{{K}_{sp}}}\]
done
clear
B)
\[{{({{K}_{sp}})}^{1/3}}\]
done
clear
C)
\[{{({{K}_{sp/4}})}^{1/3}}\]
done
clear
D)
\[{{(8{{K}_{sp}})}^{1/2}}\]
done
clear
View Answer play_arrow
question_answer 77) Equilibrium constant K, for the reaction, \[2HI(g){{H}_{2}}(g)+{{I}_{2}}(g)\] at room temperature is 2.85 and that at 698 K is \[1.4\times {{10}^{-2}}.\] This implies that the forward reaction is:
A)
exothermic
done
clear
B)
endothermic
done
clear
C)
exergonic
done
clear
D)
unpredictable
done
clear
View Answer play_arrow
question_answer 78) Which of the following represents hexadentate ligand?
A)
2, 2-bipyridyl
done
clear
B)
DMG
done
clear
C)
Ethylenediamine
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 79) The amount of substance that gives \[3.7\times {{10}^{7}}\] dps, is:
A)
one becquerel
done
clear
B)
one curie
done
clear
C)
one millicurie
done
clear
D)
one Rutherford
done
clear
View Answer play_arrow
question_answer 80) The reaction, \[A{{g}^{2+}}(aq)+Ag(s)2A{{g}^{+}}(aq)\] is an example of:
A)
reduction
done
clear
B)
oxidation
done
clear
C)
comproportionation
done
clear
D)
disproportionation
done
clear
View Answer play_arrow
question_answer 81) DDT is obtained by the reaction, of chlorobenzene with:
A)
chloral
done
clear
B)
chloroform
done
clear
C)
dichloromethane
done
clear
D)
acetaldehyde
done
clear
View Answer play_arrow
question_answer 82) Which of the following is false?
A)
Glycerol has strong hydrogen bonding
done
clear
B)
Glycol is a poisonous alcohols
done
clear
C)
Waxes are esters of higher alcohols with higher acids
done
clear
D)
Alkyl halides have higher b. p. than corresponding alcohols
done
clear
View Answer play_arrow
question_answer 83) Which of the following oxides is most acidic?
A)
\[A{{l}_{2}}{{O}_{3}}\]
done
clear
B)
\[Si{{O}_{2}}\]
done
clear
C)
\[{{P}_{2}}{{O}_{5}}\]
done
clear
D)
\[MgO\]
done
clear
View Answer play_arrow
question_answer 84) Glaubefs salt is:
A)
\[N{{a}_{2}}C{{O}_{3}}.10{{H}_{2}}O\]
done
clear
B)
\[N{{a}_{2}}S{{O}_{4}}.10{{H}_{2}}O\]
done
clear
C)
\[MgS{{O}_{4}}.7{{H}_{2}}O\]
done
clear
D)
\[CaS{{O}_{4}}.5{{H}_{2}}O\]
done
clear
View Answer play_arrow
question_answer 85) Enthalpy change when \[1\,g\]water is frozen at \[(\Delta {{H}_{fus}}=1.435\,\text{kcal}\text{mo}{{\text{l}}^{\text{-1}}})\]
A)
\[0.0797\text{ }kcal~~\]
done
clear
B)
\[-0.0797\text{ }kcal\]
done
clear
C)
\[1.435\text{ }kcal\]
done
clear
D)
\[-1.435\text{ }kcal\]
done
clear
View Answer play_arrow
question_answer 86) Which of the following statement is true?
A)
Some complex metal oxides behave as superconductor
done
clear
B)
Zinc oxide can act as superconductor
done
clear
C)
An impurity of tetravalent germanium in trivalent gallium creates electron deficiency
done
clear
D)
A Frenkel defect is formed when an ion is displaced from its lattice site to an interstitial site
done
clear
View Answer play_arrow
question_answer 87) The correct set of four quantum number for the valence electron of rubidium \[(Z=37)\] is:
A)
\[n=5,\,l=0,\,m=0,\,s=+\,1/2\]
done
clear
B)
\[n=5,\,l=1,\,m=1,\,s=+\,1/2\]
done
clear
C)
\[n=5,\,l=1,\,m=1,\,s=+\,1/2\]
done
clear
D)
\[n=6,\,l=0,\,m=0,\,s=+\,1/2\]
done
clear
View Answer play_arrow
question_answer 88) \[s{{p}^{3}}-\]hybridisation is not found in:
A)
\[{{H}_{2}}O\]
done
clear
B)
\[C{{H}_{4}}\]
done
clear
C)
\[BC{{l}_{3}}\]
done
clear
D)
\[N{{H}_{3}}\]
done
clear
View Answer play_arrow
question_answer 89) Chalcopyrites is an ore of:
A)
gallium
done
clear
B)
copper
done
clear
C)
calcium
done
clear
D)
magnesium
done
clear
View Answer play_arrow
question_answer 90) Which of the following statement is correct?
A)
Acidity increases with increase in carbon atoms in carboxylic acids
done
clear
B)
Solubility of carboxylic adds increases with increase in carbon atoms
done
clear
C)
Boiling points of acids are higher than corresponding alcohols
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 91) Which temperature is most suitable for fermentation?
A)
273 K
done
clear
B)
298 K
done
clear
C)
350 K
done
clear
D)
330 K
done
clear
View Answer play_arrow
question_answer 92) In the reaction, \[HCHO+N{{H}_{3}}\xrightarrow{{}}X,X\]is:
A)
meta-formaldehyde
done
clear
B)
para-formaldehyde
done
clear
C)
urotropine
done
clear
D)
none of the above
done
clear
View Answer play_arrow
question_answer 93) Which of the following have highest melting points?
A)
p-block elements
done
clear
B)
s-block elements
done
clear
C)
d-block elements
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 94) An acid has \[pH=5\]and its concentration is 1M. What is the value of \[{{K}_{a}}\]for the acid?
A)
\[{{10}^{-7}}\]
done
clear
B)
\[{{10}^{-5}}\]
done
clear
C)
\[{{10}^{-10}}\]
done
clear
D)
\[{{10}^{-8}}\]
done
clear
View Answer play_arrow
question_answer 95) Fatty acid is to fat as glucose is to:
A)
cellulose
done
clear
B)
glycogen
done
clear
C)
starch
done
clear
D)
all of these
done
clear
View Answer play_arrow
question_answer 96) In aerosol, the dispersion medium is:
A)
solid
done
clear
B)
liquid
done
clear
C)
gas
done
clear
D)
any of these
done
clear
View Answer play_arrow
question_answer 97) Peptisation denotes:
A)
digestion of food
done
clear
B)
hydrolysis of protein
done
clear
C)
breaking and dispersion into colloidal state
done
clear
D)
precipitation of solid from colloidal state
done
clear
View Answer play_arrow
question_answer 98) Buna-N is a polymer of:
A)
butadiene and isoprene
done
clear
B)
butadiene and acrylonitrile
done
clear
C)
isoprene and ethylene diamine
done
clear
D)
isoprene and butyl diamine
done
clear
View Answer play_arrow
question_answer 99) Which of the following is an engrain dye?
A)
Congo-red
done
clear
B)
Aniline black
done
clear
C)
Alizarin
done
clear
D)
Indigo
done
clear
View Answer play_arrow
question_answer 100) Which of the following give an explosive, RDX, on nitration?
A)
Toluene
done
clear
B)
Benzene
done
clear
C)
Guanidine
done
clear
D)
Urotropine
done
clear
View Answer play_arrow
question_answer 101) If\[f(x)=\left\{ \begin{matrix} \frac{\sin x}{x}+\cos x, & \text{when}\,\text{x}\ne \text{0} \\ 2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,, & \text{when}\,x=0 \\ \end{matrix} \right.\]
A)
\[\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,f(x)\ne 2\]
done
clear
B)
\[\underset{x\to {{0}^{-}}}{\mathop{\lim }}\,f(x)=0\]
done
clear
C)
\[f(x)\]is continuous at \[x=0\]
done
clear
D)
none of the above
done
clear
View Answer play_arrow
question_answer 102) If \[y=f(x)=\frac{x+2}{x-1},\] then \[x\] is equal to:
A)
\[f(y)\]
done
clear
B)
\[2f(y)\]
done
clear
C)
\[\frac{1}{f(y)}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 103) The value of b and c for which the identity\[f(x+1)-f(x)=8x+3\] is satisfied, where \[f(x)=b{{x}^{2}}+cx+d,\]are:
A)
\[b=2,\,c=1\]
done
clear
B)
\[b=4,c=-1\]
done
clear
C)
\[b=-1,c=4\]
done
clear
D)
\[b=-1,c=1\]
done
clear
View Answer play_arrow
question_answer 104) The range of the function \[f(x)={{x}^{2}}-6x+7\]is:
A)
\[(-\infty ,0)\]
done
clear
B)
\[[-2,\infty )\]
done
clear
C)
\[(-\infty ,\infty )\]
done
clear
D)
\[(-\infty ,-2)\]
done
clear
View Answer play_arrow
question_answer 105) If\[f(x)=x{{\tan }^{-1}}x,\] then \[f(1)\] is equal to:
A)
\[1+\frac{\pi }{4}\]
done
clear
B)
\[\frac{1}{2}+\frac{\pi }{4}\]
done
clear
C)
\[\frac{1}{2}-\frac{\pi }{4}\]
done
clear
D)
2
done
clear
View Answer play_arrow
question_answer 106) \[\frac{d}{dx}\sqrt{\frac{1-\sin 2x}{1+\sin 2x}}\]is equal to:
A)
\[{{\sec }^{2}}x\]
done
clear
B)
\[-{{\sec }^{2}}\left( \frac{\pi }{4}-x \right)\]
done
clear
C)
\[{{\sec }^{2}}\left( \frac{\pi }{4}+x \right)\]
done
clear
D)
\[{{\sec }^{2}}\left( \frac{\pi }{4}-x \right)\]
done
clear
View Answer play_arrow
question_answer 107) If \[y={{x}^{2}}+\frac{1}{{{x}^{2}}+\frac{1}{{{x}^{2}}+\frac{1}{{{x}^{2}}+...\infty }}}\,\,,\]then \[\frac{dy}{dx}\]is equal to:
A)
\[\frac{2xy}{2y-{{x}^{2}}}\]
done
clear
B)
\[\frac{xy}{y+{{x}^{2}}}\]
done
clear
C)
\[\frac{xy}{y-{{x}^{2}}}\]
done
clear
D)
\[\frac{2x}{2+\frac{{{x}^{2}}}{y}}\]
done
clear
View Answer play_arrow
question_answer 108) The function \[F(x)=\max [(1-x),(1+x),2],x\in (-\infty ,\infty )\]is:
A)
continuous at all points
done
clear
B)
differentiable at all points
done
clear
C)
differentiable at all points except at \[x=1\] and \[x=-1\]
done
clear
D)
none of the above
done
clear
View Answer play_arrow
question_answer 109) If \[f({{x}_{1}})-f({{x}_{2}})=f\left( \frac{{{x}_{1}}-{{x}_{2}}}{1-{{x}_{2}}{{x}_{2}}} \right)\]for \[{{x}_{1}},{{x}_{2}}\in [-1,1],\]then \[f(x)\]is equal to:
A)
\[{{\tan }^{-1}}\frac{(1+x)}{(1-x)}\]
done
clear
B)
\[{{\tan }^{-1}}\frac{(1-x)}{(1+x)}\]
done
clear
C)
\[\log \frac{(1+x)}{(1-x)}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 110) \[\int_{{}}^{{}}{\frac{dx}{x({{x}^{n}}+1)}}\]is equal to:
A)
\[n\log \frac{{{x}^{n}}}{{{x}^{n}}+1}+c\]
done
clear
B)
\[n\log \frac{{{x}^{n}}+1}{{{x}^{n}}}+c\]
done
clear
C)
\[\frac{1}{n}\log \frac{{{x}^{n}}}{{{x}^{n}}+1}+c\]
done
clear
D)
\[\frac{1}{n}\log \frac{{{x}^{n}}+1}{{{x}^{n}}}+c\]
done
clear
View Answer play_arrow
question_answer 111) \[\int_{{}}^{{}}{{{\{1+2\tan x(\tan x+\sec x)\}}^{1/2}}dx}\]is equal to:
A)
\[log(sec\text{ }x+tan\text{ }x)+c\]
done
clear
B)
\[log{{(sec\text{ }x+tan\text{ }x)}^{1/2}}+\text{ }c\]
done
clear
C)
\[~log\,sec\text{ }x\,(sec\text{ }x+tan\text{ }x)+c\]
done
clear
D)
none of the above
done
clear
View Answer play_arrow
question_answer 112) The value of \[\int_{0}^{\pi /2}{\frac{\cos \theta }{\sqrt{4-{{\sin }^{2}}\theta }}}d\theta \]is:
A)
\[\frac{\pi }{2}\]
done
clear
B)
\[\frac{\pi }{6}\]
done
clear
C)
\[\frac{\pi }{3}\]
done
clear
D)
\[\frac{\pi }{5}\]
done
clear
View Answer play_arrow
question_answer 113) If the ordinate\[x=a\] divides the area bounded by the curve\[y=\left( 1+\frac{8}{{{x}^{2}}} \right),\]\[x-\]axis and the ordinates \[x=2,\text{ }x=4,\]into two equal parts, then the value of a is:
A)
2a
done
clear
B)
\[2\sqrt{2}\]
done
clear
C)
\[\frac{a}{2}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 114) Area included between the two curves, \[{{y}^{2}}=4ax\]and \[{{x}^{2}}-4ay\]is equal to:
A)
\[\frac{32}{3}{{a}^{2}}\text{sq}\,\text{unit}\]
done
clear
B)
\[\frac{64}{9}\,\text{sq}\,\text{unit}\]
done
clear
C)
\[\frac{32}{3}\text{sq}\,\text{unit}\]
done
clear
D)
\[\frac{16}{3}{{a}^{2}}\text{sq}\,\text{unit}\]
done
clear
View Answer play_arrow
question_answer 115) The differential equation of the family of curves \[y=a\cos (x+b)\]is :
A)
\[\frac{{{d}^{2}}y}{d{{x}^{2}}}-y=0\]
done
clear
B)
\[\frac{{{d}^{2}}y}{d{{x}^{2}}}+y=0\]
done
clear
C)
\[\frac{{{d}^{2}}y}{d{{x}^{2}}}+2y=0\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 116) The solution of the given differential equation\[\frac{dy}{dx}+2xy=y\]is:
A)
\[y=c{{e}^{x-{{x}^{2}}}}\]
done
clear
B)
\[y=c{{e}^{{{x}^{2}}-x}}\]
done
clear
C)
\[y=c{{e}^{x}}\]
done
clear
D)
\[y=c{{e}^{-{{x}^{2}}}}\]
done
clear
View Answer play_arrow
question_answer 117) If the probability of X to fail in the examination is 0.3 and that for Y is 0.2, then the probability that either X or Y fail in examination is:
A)
0.5
done
clear
B)
0.44
done
clear
C)
0.6
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 118) The plane\[\frac{x}{2}+\frac{y}{3}+\frac{z}{4}=1\] cuts the coordinate axes in A, B, C, then the area of the \[\Delta ABC\]is:
A)
\[\sqrt{29}\] sq unit
done
clear
B)
\[\sqrt{41}\,\text{sq}\,\text{unit}\]
done
clear
C)
\[\sqrt{61}\,\text{sq}\,\text{unit}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 119) Let \[~0<P(A)<1,0<P(B)<1~\] and \[P(A\cap B)=P(A)+P(B)-P(A)P(B),\]then:
A)
\[P(B/A)=P(B)-P(A)\]
done
clear
B)
\[P({{A}^{c}}\cup {{B}^{c}})=P({{A}^{c}})+P({{B}^{c}})\]
done
clear
C)
\[P{{(A\cup B)}^{c}}=P({{A}^{c}})P({{B}^{c}})\]
done
clear
D)
\[P(A/B)=P(A)+P({{B}^{c}})\]
done
clear
View Answer play_arrow
question_answer 120) If the plane \[x+2y+2z-15=0\]cuts the sphere \[{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2y-4z-11=0,\]then the radius of the circle is:
A)
\[\sqrt{3}\]
done
clear
B)
\[\sqrt{5}\]
done
clear
C)
\[\sqrt{7}\]
done
clear
D)
\[\sqrt{11}\]
done
clear
View Answer play_arrow
question_answer 121) Forces acting on a particle have a magnitude 5, 3 and 1 unit and act in the direction of the vectors \[6\hat{i}+2\hat{j}+3\hat{k},3\hat{i}-4\hat{j}+6\hat{k}\] and \[2\hat{i}-3\hat{j}-6\hat{k}\]respectively. Then remain constant while the particle is displaced from the point \[A(2,-1,-3)\]to \[B(5,-1,-1),\]The work done is:
A)
11 unit
done
clear
B)
33 unit
done
clear
C)
10 unit
done
clear
D)
30 unit
done
clear
View Answer play_arrow
question_answer 122) If \[\vec{a},\vec{b},\vec{c}\]are three non-coplanar vectors, then the vector equation\[\vec{r}=(1-p-q)\vec{a}+p\vec{b}+q\vec{c}\] represents a:
A)
straight line
done
clear
B)
plane
done
clear
C)
plane passing through the origin
done
clear
D)
sphere
done
clear
View Answer play_arrow
question_answer 123) If angle between \[\vec{a}\]and\[\vec{b}\]is\[\frac{2\pi }{3}\] and if\[|\vec{a}|=5,|\vec{b}|=3,\]then\[|\vec{a}-\vec{b}|\]is equal to:
A)
23
done
clear
B)
7
done
clear
C)
17
done
clear
D)
18
done
clear
View Answer play_arrow
question_answer 124) Let p and q be two statements, then \[(p\ \vee q)\vee \tilde{\ }p\] is:
A)
tautology
done
clear
B)
contradiction
done
clear
C)
both (a) and (b)
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 125) The values of \[x\] and \[y\]satisfying the equation \[\frac{(1+i)x-2i}{3+i}+\frac{(2-3i)y+i}{3-i}=i\]are:
A)
\[x=-1,y=3\]
done
clear
B)
\[x=3,y=-1\]
done
clear
C)
\[x=0,y=1\]
done
clear
D)
\[x=1,y=0\]
done
clear
View Answer play_arrow
question_answer 126) The points \[{{z}_{1}},{{z}_{2}},{{z}_{3}},{{z}_{4}}\]in the complex plane are the vertices of a parallelogram taken in order, iff:
A)
\[{{z}_{1}}+{{z}_{4}}={{z}_{2}}+{{z}_{3}}\]
done
clear
B)
\[{{z}_{1}}+{{z}_{3}}={{z}_{2}}+{{z}_{4}}\]
done
clear
C)
\[{{z}_{1}}+{{z}_{2}}={{z}_{3}}+{{z}_{4}}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 127) An OR gate is the boolean function defined of:
A)
\[f({{x}_{1}},{{x}_{2}})={{x}_{1}}{{x}_{2}};{{x}_{1}},{{x}_{2}}\in \{0,1\}\]
done
clear
B)
\[f({{x}_{1}},{{x}_{2}})={{x}_{1}}+{{x}_{2}};{{x}_{1}},{{x}_{2}}\in \{0,1\}\]
done
clear
C)
\[f({{x}_{1}},{{x}_{2}})={{x}_{1}};{{x}_{1}},{{x}_{2}}\in \{0,1\}\]
done
clear
D)
\[f({{x}_{1}},{{x}_{2}})={{x}_{2}};{{x}_{1}},{{x}_{2}}\in \{0,1\}\]
done
clear
View Answer play_arrow
question_answer 128) If the sum of the roots of the equation \[a{{x}^{2}}+bx+c=0\]be equal to the sum of the reciprocal of their squares, then \[b{{c}^{2}},c{{a}^{2}},a{{b}^{2}}\]will be in:
A)
AP
done
clear
B)
GP
done
clear
C)
HP
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 129) If\[x,y,z\] are in GP and \[{{a}^{x}}={{b}^{y}}={{c}^{z}},\]then:
A)
\[{{\log }_{a}}C={{\log }_{b}}a\]
done
clear
B)
\[{{\log }_{b}}a={{\log }_{c}}b\]
done
clear
C)
\[{{\log }_{c}}b={{\log }_{a}}c\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 130) The sum of the series \[1+\frac{1}{5}+\frac{1.3}{5.10}+\frac{1.3.5}{5.10.15}+....\]is equal to:
A)
\[\frac{1}{\sqrt{5}}\]
done
clear
B)
\[\frac{1}{\sqrt{2}}\]
done
clear
C)
\[\sqrt{3}\]
done
clear
D)
\[\sqrt{\frac{5}{3}}\]
done
clear
View Answer play_arrow
question_answer 131) If \[x\]is real, then the value of \[\frac{x+2}{2{{x}^{2}}+3x+6}\]
A)
\[\left( \frac{1}{13},\frac{1}{3} \right)\]
done
clear
B)
\[\left[ -\frac{1}{13},\frac{1}{3} \right]\]
done
clear
C)
\[\left( -\frac{1}{3},\frac{1}{13} \right)\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 132) Let a and P be the roots of the equation \[{{x}^{2}}+x+1=0,\]then the equation whose roots area\[{{\alpha }^{19}},{{\beta }^{7}}\] is:
A)
\[~{{x}^{2}}-x-1=0\]
done
clear
B)
\[~{{x}^{2}}-\text{ }x+1=0\]
done
clear
C)
\[~{{x}^{2}}+x-1=0\]
done
clear
D)
\[~{{x}^{2}}+\text{ }x+1=0\]
done
clear
View Answer play_arrow
question_answer 133) For a particle moving in a straight line, if timer be regarded as a function of velocity v, then the rate of change of the acceleration a is given by:
A)
\[{{a}^{2}}\frac{{{d}^{2}}t}{d{{v}^{2}}}\]
done
clear
B)
\[{{a}^{3}}\frac{{{d}^{2}}t}{d{{v}^{2}}}\]
done
clear
C)
\[-{{a}^{3}}\frac{{{d}^{2}}t}{d{{v}^{2}}}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 134) \[{{\,}^{47}}{{C}_{4}}+\sum\limits_{r=1}^{5}{{{\,}^{52-r}}{{C}_{3}}}\]is equal to:
A)
\[{{\,}^{47}}{{C}_{6}}\]
done
clear
B)
\[{{\,}^{52}}{{C}_{5}}\]
done
clear
C)
\[{{\,}^{52}}{{C}_{4}}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 135) In how many ways can 21 English and 19 Hindi books be placed in a row so that no two Hindi books are together:
A)
1540
done
clear
B)
1450
done
clear
C)
1504
done
clear
D)
1405
done
clear
View Answer play_arrow
question_answer 136) How many words can be made from the letters of the word COMMITTEE:
A)
\[\frac{9!}{{{(2!)}^{2}}}\]
done
clear
B)
\[\frac{9!}{{{(2!)}^{3}}}\]
done
clear
C)
\[\frac{9!}{2!}\]
done
clear
D)
9!
done
clear
View Answer play_arrow
question_answer 137) Three forces P, Q, and R acting on a particle are in equilibrium. If the angle between P and Q is double the angle between P and R, then P is equal to:
A)
\[\frac{{{Q}^{2}}+{{R}^{2}}}{R}\]
done
clear
B)
\[\frac{{{Q}^{2}}-{{R}^{2}}}{Q}\]
done
clear
C)
\[\frac{{{Q}^{2}}-{{R}^{2}}}{R}\]
done
clear
D)
\[\frac{{{Q}^{2}}+{{R}^{2}}}{Q}\]
done
clear
View Answer play_arrow
question_answer 138) If n is an integer greater than 1, then \[a-{{\,}^{n}}{{C}_{1}}(a-1)+{{\,}^{n}}{{C}_{2}}(a-2)-....+{{(-1)}^{n}}(a-n)\] is equal to:
A)
\[a\]
done
clear
B)
\[0\]
done
clear
C)
\[{{a}^{2}}\]
done
clear
D)
\[{{2}^{n}}\]
done
clear
View Answer play_arrow
question_answer 139) Forces forming a couple are of magnitude 12N each and the arm of the couple is 8m. The tone of an equivalent couple whose arm is 6 m is of magnitude:
A)
8 N
done
clear
B)
16 N
done
clear
C)
12 N
done
clear
D)
4 N
done
clear
View Answer play_arrow
question_answer 140) In the expansion of \[2{{\log }_{e}}x-{{\log }_{e}}(x+1)-{{\log }_{e}}(x-1)\] the coefficient of \[{{x}^{-4}}\]is:
A)
\[\frac{1}{2}\]
done
clear
B)
\[-1\]
done
clear
C)
1
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 141) A tower subtends an angle \[\alpha \]at a point in the plane of its base and the angle of depression of the foot of the tower at a point b ft just above A is \[\beta .\]Then height of the tower is:
A)
\[b\text{ }tan\text{ }\alpha \text{ }cot\beta \]
done
clear
B)
\[~b\text{ }cot\text{ }\alpha \text{ }tan\text{ }\beta \]
done
clear
C)
\[b\text{ }tan\text{ }\alpha \text{ }tan\text{ }\beta \]
done
clear
D)
\[b\cot \alpha \cot \beta \]
done
clear
View Answer play_arrow
question_answer 142) The matrix \[\left[ \begin{matrix} 2 & 5 & -7 \\ 0 & 3 & 11 \\ 0 & 0 & 9 \\ \end{matrix} \right]\]is known as:
A)
symmetric matrix
done
clear
B)
upper triangular matrix
done
clear
C)
diagonal matrix
done
clear
D)
skew-symmetric matrix
done
clear
View Answer play_arrow
question_answer 143) Two bodies of different masses \[{{m}_{1}}\]and \[{{m}_{2}}\]are dropped from different heights \[{{h}_{1}}\]and \[{{h}_{2}}.\]he ratio of the times taken by the two bodies to fall through these distance is:
A)
\[{{h}_{1}}:{{h}_{2}}\]
done
clear
B)
\[\sqrt{{{h}_{1}}}:\sqrt{{{h}_{2}}}\]
done
clear
C)
\[{{h}_{1}}^{2}:h_{2}^{2}\]
done
clear
D)
\[{{h}_{2}}:{{h}_{1}}\]
done
clear
View Answer play_arrow
question_answer 144) Matrix A is such that \[{{A}^{2}}=2A-I,\]where\[I\]is the identity matrix, then for \[n\ge 2,{{A}^{n}}\]is equal to:
A)
\[nA-(n-1)I\]
done
clear
B)
\[nA-I\]
done
clear
C)
\[{{2}^{n-1}}A-(n-1)I\]
done
clear
D)
\[{{2}^{n-1}}A-I\]
done
clear
View Answer play_arrow
question_answer 145) The value of the determinant \[\left| \begin{matrix} x & a & b+c \\ x & b & c+a \\ x & c & a+b \\ \end{matrix} \right|=0\]if:
A)
\[x=a\]
done
clear
B)
\[x=b\]
done
clear
C)
\[x=c\]
done
clear
D)
\[x\]has any value
done
clear
View Answer play_arrow
question_answer 146) \[{{12}^{o}}\sin {{48}^{o}}\sin {{54}^{o}}\]is equal to:
A)
1/16
done
clear
B)
1/32
done
clear
C)
1/8
done
clear
D)
1/4
done
clear
View Answer play_arrow
question_answer 147) If\[\tan A=\frac{1-\cos B}{\sin B}.\]then:
A)
\[\tan 2A=\tan B\]
done
clear
B)
\[\tan 2A=ta{{n}^{2}}B\]
done
clear
C)
\[\tan 2A={{\tan }^{2}}B+2\tan B\]
done
clear
D)
none of the above
done
clear
View Answer play_arrow
question_answer 148) Three points are\[A(6,3),B(-3,5),C(4,-2)\]and \[P(x,y)\]is any point, then the ratio of area of \[\Delta PBC\]and \[\Delta ABC\]is:
A)
\[\frac{x+y-2}{7}\]
done
clear
B)
\[\frac{x-y+2}{2}\]
done
clear
C)
\[\frac{x-y-2}{7}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 149) The circle \[{{x}^{2}}+{{y}^{2}}+4x-4y+4=0\]t touches:
A)
\[x-\]axis
done
clear
B)
\[y-\]axis
done
clear
C)
\[x-\] axis and \[y-\]axis
done
clear
D)
none of the above
done
clear
View Answer play_arrow
question_answer 150) Three normals to the parabola \[{{y}^{2}}=x\]are drawn a point (c, 0), then:
A)
\[c=\frac{1}{4}\]
done
clear
B)
\[c=\frac{1}{2}\]
done
clear
C)
\[c>\frac{1}{2}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
 1.5
1.5 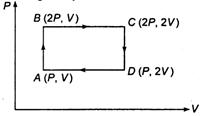
 \[R\]
\[R\] 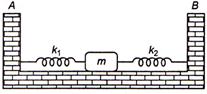
 The capacitance of capacitor will be:
The capacitance of capacitor will be: