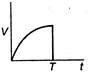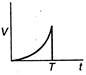question_answer 1) How much energy is absorbed by 10 kg molecule of an ideal gas, if it expands from an initial pressure of 8 atm to 4 atm at a constant temperature of\[27{}^\circ C\]?
A)
\[1.728\times {{10}^{7}}J\]
done
clear
B)
\[2.8\times {{10}^{6}}J\]
done
clear
C)
\[5J\]
done
clear
D)
\[10J\]
done
clear
E)
\[15J\]
done
clear
View Answer play_arrow
question_answer 2) The rate at which a black body emits radiation at a temperature T is proportional to:
A)
\[1/T\]
done
clear
B)
T
done
clear
C)
\[{{T}^{3}}\]
done
clear
D)
\[1/{{T}^{4}}\]
done
clear
E)
\[{{T}^{4}}\]
done
clear
View Answer play_arrow
question_answer 3) Two equal charges q are kept fixed at a and +a along the\[x-\]axis. A particle of mass m and change\[\frac{q}{2}\]is brought to the origin and given a small displacement along the\[x-\]axis, then:
A)
the particle executes oscillatory motion
done
clear
B)
the particle remains stationary
done
clear
C)
the particle executes, SUM along\[x-\]axis
done
clear
D)
the particle executes SHM along y-axis
done
clear
E)
the particle moves on circular path
done
clear
View Answer play_arrow
question_answer 4) Two equal point changes,\[Q=+\sqrt{2}\mu C\]are placed at each of the two opposite corners of a square and equal point charges q at each of the other two comers. The value of q, so that the resultant force on Q is zero is:
A)
\[+0.5\mu C\]
done
clear
B)
\[-0.5\mu C\]
done
clear
C)
\[1\mu C\]
done
clear
D)
\[-1\mu C\]
done
clear
E)
none of above
done
clear
View Answer play_arrow
question_answer 5) At great distances from an electric dipole, the electric field strength due to the dipole varies with the distance as:
A)
\[\frac{1}{r}\]
done
clear
B)
\[\frac{1}{{{r}^{2}}}\]
done
clear
C)
\[\frac{1}{{{r}^{3}}}\]
done
clear
D)
\[\frac{1}{{{r}^{4}}}\]
done
clear
E)
\[\frac{1}{{{r}^{6}}}\]
done
clear
View Answer play_arrow
question_answer 6) Two capacitors, one 4 pF and the other 6 pF, connected in parallel, are charged by a 100 V battery. The energy stored in the capacitors is:
A)
\[1.2\times {{10}^{-8}}J\]
done
clear
B)
\[2.4\times {{10}^{-8}}J\]
done
clear
C)
\[5.0\,\times {{10}^{-8}}J\]
done
clear
D)
\[1.2\times {{10}^{-6}}J\]
done
clear
E)
\[5.0\times {{10}^{-6}}J\]
done
clear
View Answer play_arrow
question_answer 7) A solid sphere of radius R has a charge Q uniformly distributed throughout its volume. For distances\[r<R\]from the centre of the sphere, the electric field strength varies with distance as:
A)
\[1/{{r}^{3}}\]
done
clear
B)
\[1/{{r}^{2}}\]
done
clear
C)
\[1/r\]
done
clear
D)
\[r\]
done
clear
E)
\[r{}^\circ ,\]i.e., it is constant
done
clear
View Answer play_arrow
question_answer 8) A potentiometer is a device for:
A)
measuring potential energy
done
clear
B)
measuring currents
done
clear
C)
measuring electrical power
done
clear
D)
comparing emf of two sources
done
clear
E)
comparing two resistances
done
clear
View Answer play_arrow
question_answer 9) The electrical resistivity of a sample:
A)
is proportional to its length
done
clear
B)
is proportional to the area of cross-section
done
clear
C)
is inversely proportional to the length
done
clear
D)
is inversely proportional to the area of cross-section
done
clear
E)
neither depends on the length nor on the area of cross-section
done
clear
View Answer play_arrow
question_answer 10) A thin wire of length 0.2 m and mass\[5\,\mu g\]remains suspended in air between the pieces of a magnet. If the wire is carrying a current of 0.5 A, the strength of the magnetic field is: (take\[=10m/{{s}^{2}}\])
A)
50 gauss
done
clear
B)
5 gauss
done
clear
C)
0.5 gauss
done
clear
D)
0.05 gauss
done
clear
E)
0.005 gauss
done
clear
View Answer play_arrow
question_answer 11) A voltmeter of resistance\[998\,\Omega \]is connected across a cell of emf 2V and internal resistance\[2\,\Omega \]. The potential difference across the voltmeter is:
A)
1.99V
done
clear
B)
3.5 V
done
clear
C)
5V
done
clear
D)
6 V
done
clear
E)
1.5V
done
clear
View Answer play_arrow
question_answer 12) Two thin long parallel wires, separated by a distance d carry current i (amperes) each. The magnitude of the force per unit length exerted by one wire on the other is:
A)
\[{{\mu }_{0}}{{i}^{2}}/2\pi d\]
done
clear
B)
\[{{\mu }_{0}}{{i}^{2}}/4\pi d\]
done
clear
C)
\[{{\mu }_{0}}{{i}^{2}}/2\pi d\]
done
clear
D)
\[{{\mu }_{0}}i/4\pi d\]
done
clear
E)
\[{{\mu }_{0}}{{i}^{2}}/2\pi d\]
done
clear
View Answer play_arrow
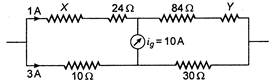
question_answer 13)
In the adjoining circuit, the resistance are given in ohms X and Y are unknown resistances. The current through the 100 resistance is 3A, while that through the resistance X is 1A. No current passes through the galvanometer. The values of the unknown resistance X and Y are. respectively:
A)
\[12\,\Omega \]and\[12\,\Omega \]
done
clear
B)
\[12\,\Omega \] and\[6\,\Omega \]
done
clear
C)
\[6\,\Omega \]and\[12\,\Omega \]
done
clear
D)
\[6\,\Omega \]and\[6\,\Omega \]
done
clear
E)
\[14\,\Omega \]and \[54\,\Omega \]
done
clear
View Answer play_arrow
question_answer 14) A heater A gives out 300 W of heat when connected to a 200 V DC supply. A second heater B gives out 600 W when connected to a 200 V DC, supply. If a series combination of the two heaters is connected to a 200 V DC supply, the heat output will be:
A)
900 W
done
clear
B)
450 W
done
clear
C)
300 W
done
clear
D)
200 W
done
clear
E)
100 W
done
clear
View Answer play_arrow
question_answer 15) A charged particle travels along a straight line with a speed v in a region where both electric field\[\overrightarrow{E}\]and magnetic fields\[\overrightarrow{B}\]are present. It follows that:
A)
\[|\overrightarrow{E}|=v|\overrightarrow{B}|\]and the two fields are parallel
done
clear
B)
\[|\overrightarrow{E}|=v|\overrightarrow{B}|\]and the two fields are perpendicular
done
clear
C)
\[|\overrightarrow{B}|=v|\overrightarrow{E}|\]and the two fields are parallel
done
clear
D)
\[|\overrightarrow{B}|=v|\overrightarrow{E}|\]and the two fields are perpendicular
done
clear
E)
\[|\overrightarrow{E}|=|\overrightarrow{B}|\]and the two fields are perpendicular
done
clear
View Answer play_arrow
question_answer 16) A solenoid of length 50 cm and a radius of cross-section 1 cm has 1000 turns of wire wound over it. If the current carried is 5 A, the magnetic field on its axis, near the centre of the solenoid is approximately (permeability of free space\[{{\mu }_{0}}=4\pi \times {{10}^{-7}}T-m/A)\]:
A)
\[0.63\times {{10}^{-2}}T\]
done
clear
B)
\[1.26\times {{10}^{-2}}T\]
done
clear
C)
\[2.51\times {{10}^{-2}}T\]
done
clear
D)
\[6.3T\]
done
clear
E)
\[12.6\text{ }T\]
done
clear
View Answer play_arrow
question_answer 17) A short bar magnet with a magnetic moment of\[0.5\text{ }J/T\]is placed in a uniform external magnetic field of 0.16 T in such a way that the magnetic moment vector is anti-parallel to the direction of the magnetic field. The potential energy of the bar magnet is:
A)
0.32 J
done
clear
B)
0.16 J
done
clear
C)
0.08 J
done
clear
D)
\[-0.08J\]
done
clear
E)
\[-0.32J\]
done
clear
View Answer play_arrow
question_answer 18) A conducting square loop of side L and resistance R moves in its plane with a uniform velocity v, perpendicular to one of its sides. A magnetic field of induction B, constant in space and time and pointing perpendicularly into the plane of the square, exists every where in space. The current induced in the loop is:
A)
\[BLv/R\] in the clockwise direction
done
clear
B)
\[BLv/R\] in the anticlockwise direction
done
clear
C)
\[2BLv/R\] in the clockwise direction
done
clear
D)
\[2BLv/R\]in the anticlockwise direction
done
clear
E)
zero
done
clear
View Answer play_arrow
question_answer 19) A solenoid has an inductance of 50 mH and a resistance of\[0.4\,\Omega \]. If the solenoid is connected to a battery, the time taken for the current to reach one-half its equilibrium value is (in seconds):
A)
\[0.8\,ln2\]
done
clear
B)
\[\ln \,2\]
done
clear
C)
\[0.125\,\ln \,2\]
done
clear
D)
\[0.25\,\ln \,2\]
done
clear
E)
\[12\,\ln \,2\]
done
clear
View Answer play_arrow
question_answer 20) A sinusoidal voltage of peak value 300 V and an angular frequency\[\omega =400\]rad/s is applied to a series L-C-R circuit, in which\[R=3\Omega ,\]\[L=20\text{ }mH\]and\[C=625\,\mu F\]The peak current in the circuit is
A)
\[30\sqrt{2}A\]
done
clear
B)
\[60A\]
done
clear
C)
\[100A\]
done
clear
D)
\[60\sqrt{2}A\]
done
clear
E)
\[100\sqrt{2}A\]
done
clear
View Answer play_arrow
question_answer 21) A circuit contains a capacitor and inductance each with negligible resistance. The capacitor is initially charged and the charging battery is disconnected. At subsequent time, the charge on the capacitor will:
A)
increase exponentially
done
clear
B)
decrease exponentially
done
clear
C)
decrease linearly
done
clear
D)
remain constant
done
clear
E)
oscillate with a characteristic frequency
done
clear
View Answer play_arrow
question_answer 22) A transformer of 100% efficiency has 200 turns in the primary and 40000 turns in secondary is connected to a 220 V main supply and secondary feeds to a\[100\,k\Omega \]resistance. The Potential difference per turn is respectively:
A)
\[1.1\,V\]
done
clear
B)
\[25V\]
done
clear
C)
\[18\,V\]
done
clear
D)
\[11\,V\]
done
clear
E)
\[35V\]
done
clear
View Answer play_arrow
question_answer 23) A plane electromagnetic wave travels in vacuum along\[\hat{k}\]direction, where\[\hat{i},\hat{j}\]and\[\hat{k}\]are unit vectors along the\[x,\text{ }y\]and z directions and z directions. The direction along which the electric and the magnetic field vectors point may be respectively:
A)
\[\hat{i}\,and\,\hat{j}\]
done
clear
B)
\[\hat{i}\,and\,-\hat{j}\]
done
clear
C)
\[\hat{j}\,\,and\,\hat{i}\]
done
clear
D)
\[\hat{k}\,\,and\,\hat{i}\]
done
clear
E)
\[\hat{k}\,\,and\,\hat{j}\]
done
clear
View Answer play_arrow
question_answer 24) In the order of increasing frequency, the electromagnetic spectrum may be arranged as:
A)
gamma rays, X-rays, visible light, radio waves
done
clear
B)
X-rays, gamma rays, visible light, radio waves
done
clear
C)
radio waves, visible light, X-rays, gamma
done
clear
D)
radio waves, visible light, gamma rays,
done
clear
E)
gamma rays. X-rays, radio waves, visible
done
clear
View Answer play_arrow
question_answer 25) Two coherent monochromatic light beams of intensities\[I\]and \[9I\]are super imposed. The maximum and the minimum intensities of the resultant beam are:
A)
\[10I\]and zero
done
clear
B)
\[10I\]and\[8I\]
done
clear
C)
\[10I\]and\[4I\]
done
clear
D)
\[16I\]and\[4I\]
done
clear
E)
\[16I\]and zero
done
clear
View Answer play_arrow
question_answer 26) In a single slit diffraction pattern-the distance between the first minimum on the left and the first minimum on the right is 5 mm. The Screen on which the diffraction pattern is displayed at a distance of 80 cm from the slit The length is \[6000\overset{\text{o}}{\mathop{\text{A}}}\,\].The slit width in (mm) is about:
A)
\[0.576\]
done
clear
B)
\[0.348\]
done
clear
C)
\[0.192\]
done
clear
D)
\[0.096\]
done
clear
E)
\[0.048\]
done
clear
View Answer play_arrow
question_answer 27) When a ray is incident on a medium of refractive index n at Brewsters angle, it gets:
A)
totally reflected
done
clear
B)
totally absorbed
done
clear
C)
circularly polarised
done
clear
D)
plane polarised
done
clear
E)
elliptically polarised
done
clear
View Answer play_arrow
question_answer 28) An object is placed at a distance of 30 cm from a concave mirror and its real image is formed at a distance of 30 cm from the mirror. The focal length of the mirror is:
A)
60 cm
done
clear
B)
45 cm
done
clear
C)
30cm
done
clear
D)
20cm
done
clear
E)
15cm
done
clear
View Answer play_arrow
question_answer 29) A converging lens has a focal length of 50 cm The power of the lens is:
A)
\[+5D\]
done
clear
B)
\[+2D\]
done
clear
C)
\[+0.5D\]
done
clear
D)
\[-0.5D\]
done
clear
E)
\[-2D\]
done
clear
View Answer play_arrow
question_answer 30) A converging lens of focal length\[f\]is used as simple microscope. If the least distance of district vision of the observer is D and the lens is held close to the eye, the magnifying power of the lens is:
A)
\[D/2f\]
done
clear
B)
\[f/D\]
done
clear
C)
\[\frac{D}{f}-1\]
done
clear
D)
\[D/f\]
done
clear
E)
\[\frac{f}{D}+1\]
done
clear
View Answer play_arrow
question_answer 31) A thin convex lens of refractive index 1.5 has 20 cm focal length in air. If the lens is completely immersed in liquid of refractive index 1.6, its focal length will be:
A)
\[-160cm\]
done
clear
B)
\[-100cm\]
done
clear
C)
\[+10\text{ }cm\]
done
clear
D)
\[+100cm\]
done
clear
E)
\[+\text{ }160\text{ }cm\]
done
clear
View Answer play_arrow
question_answer 32) In Thomsons experiment to measure e/m of electron, the electric and the magnetic fields are:
A)
in the same direction
done
clear
B)
in the opposite direction
done
clear
C)
at an angle of\[45{}^\circ \] with each other
done
clear
D)
at an angle of\[60{}^\circ \]with each other
done
clear
E)
perpendicular to each other
done
clear
View Answer play_arrow
question_answer 33) The photoelectric cut-off voltage in an experiment was found to be 1.5 V. The work function for the material used in the experiment was 4.2 eV. The maximum kinetic energy of the photoelectrons that was emitted was:
A)
1.5 eV
done
clear
B)
2.7 eV
done
clear
C)
4.2 eV
done
clear
D)
5.7 eV
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 34) A photo cell is a device which:
A)
absorbs light and produces a stream of electrons
done
clear
B)
absorb a stream of electron and produces light
done
clear
C)
converts protons into photons
done
clear
D)
converts photons into protons
done
clear
E)
converts visible light into gamma rays
done
clear
View Answer play_arrow
question_answer 35) The ground state energy of hydrogen atom is\[-\,13.6\text{ }eV\]. The kinetic energy of the electron in this state is:
A)
27.2 eV
done
clear
B)
13.6 eV
done
clear
C)
6.8 eV
done
clear
D)
3.4 eV
done
clear
E)
1.85 eV
done
clear
View Answer play_arrow
question_answer 36) When an atom undergoes\[\beta -\]decay, its atomic number:
A)
does not change
done
clear
B)
increases by 1
done
clear
C)
decreases by 1
done
clear
D)
increases by 2
done
clear
E)
decreases by 2
done
clear
View Answer play_arrow
question_answer 37) A nucleus X initially at rest, undergoes alpha decay according to the equation \[_{92}{{X}^{A}}{{\xrightarrow{{}}}_{z}}{{Y}^{228}}+\alpha \] Then, the values of A and Z are:
A)
94, 230
done
clear
B)
232, 90
done
clear
C)
190, 32
done
clear
D)
230, 94
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 38) The energy gap between the valence band and the conduction band for a material is\[6\text{ }eV\]. The material is:
A)
an insulator
done
clear
B)
a metal
done
clear
C)
an intrinsic semiconductor
done
clear
D)
a superconductor
done
clear
E)
a doped semiconductor
done
clear
View Answer play_arrow
question_answer 39) An AC signal of 50 Hz frequency is input of a full wave rectifier using two diodes. The output frequency after full wave rectification is:
A)
25 Hz
done
clear
B)
50 Hz
done
clear
C)
100 Hz
done
clear
D)
200 Hz
done
clear
E)
Zero i.e., the output is DC
done
clear
View Answer play_arrow
question_answer 40) In a transistor biased in the common-emitter mode the emitter current is:
A)
much smaller than base current
done
clear
B)
much larger than base current
done
clear
C)
nearly equal to the base current
done
clear
D)
much smaller than the collector current
done
clear
E)
much larger than the collector current
done
clear
View Answer play_arrow
question_answer 41) When the inputs of a two input logic gate are 0 and 0, the output is 1. When the inputs are 1 and 0 the output is 0. The logic gate is of the type:
A)
AND
done
clear
B)
NAND
done
clear
C)
NOR
done
clear
D)
OR
done
clear
E)
XOR
done
clear
View Answer play_arrow
question_answer 42) The sun revolves around galaxy with speed of 250 km/s around the centre of Milky Way and its radius is\[3\times {{10}^{4}}\]light year. The mass of milky way in (kg) is:
A)
\[6\times {{10}^{41}}\]
done
clear
B)
\[5\times {{10}^{41}}\]
done
clear
C)
\[4\times {{10}^{41}}\]
done
clear
D)
\[3\times {{10}^{41}}\]
done
clear
E)
\[2\times {{10}^{41}}\]
done
clear
View Answer play_arrow
question_answer 43) The dimensions of the quantity\[hv/c,\]where h is Plancks constant, v is the frequency and c is the velocity of light is:
A)
\[[M{{T}^{-1}}]\]
done
clear
B)
\[[ML{{T}^{-1}}]\]
done
clear
C)
\[[ML{{T}^{-2}}]\]
done
clear
D)
\[[M{{L}^{2}}{{T}^{2}}]\]
done
clear
E)
\[[M{{L}^{-2}}{{T}^{-2}}]\]
done
clear
View Answer play_arrow
question_answer 44) The SI unit of the coefficient of viscosity is:
A)
\[N-{{m}^{2}}\]
done
clear
B)
\[N-s\]
done
clear
C)
\[N-s/{{m}^{2}}\]
done
clear
D)
\[N-{{m}^{2}}/s\]
done
clear
E)
\[N-{{m}^{2}}-s\]
done
clear
View Answer play_arrow
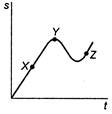
question_answer 45)
A particle is constrained to move along a straight line. The graph in the adjoining figure shows the distance s moved by the particle in time r, measured from the starting time. The shape of the curve indicates that:
A)
acceleration of the particle is increasing at X
done
clear
B)
the speed of the particle is maximum at the point Z
done
clear
C)
the speed of the particle X is greater than that at Z
done
clear
D)
the acceleration of the particle is decreasing at X
done
clear
E)
the particle is at rest at the point Y
done
clear
View Answer play_arrow
question_answer 46) A bomb is fixed from a canon with a velocity of 1000 m/s making an angle of\[30{}^\circ \]with the horizontal\[(g=9.8\text{ }m/{{s}^{2}})\]. Time taken by bomb to reach the highest point is:
A)
40 s
done
clear
B)
30 s
done
clear
C)
51 s
done
clear
D)
25 s
done
clear
E)
15s
done
clear
View Answer play_arrow
question_answer 47) A particle is acted upon by a force of constant magnitude which is always perpendicular to the velocity of the particle. The motion of the particle takes place in the plane. It follows that:
A)
the speed of the particle is constant
done
clear
B)
the acceleration of the particle is constant
done
clear
C)
the motion is that of a projectile
done
clear
D)
the velocity of the particle is constant
done
clear
E)
the kinetic energy of the particle changes with time
done
clear
View Answer play_arrow
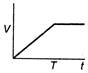
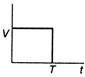
question_answer 48) A body is acted upon by a constant force from time\[t=0\]to a time\[t=T\]after which it does not experience any force. Which of the following graphs best represents the variation of the velocity of the body with time?
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
E)
done
clear
View Answer play_arrow
question_answer 49) A satellite is in a circular orbit round the earth at an altitude R above the earths surface, where R is the radius of the earth. If g is the acceleration due to gravity on the surface of the earth the speed of the satellite is:
A)
\[\sqrt{2Rg}\]
done
clear
B)
\[\sqrt{Rg}\]
done
clear
C)
\[\sqrt{Rg/2}\]
done
clear
D)
\[\sqrt{Rg/4}\]
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 50) At the top of the trajectory of a projectile, thrown at an angle of projection\[\theta <90{}^\circ ,\] its:
A)
velocity is zero
done
clear
B)
velocity is parallel to the direction of acceleration
done
clear
C)
velocity is anti-parallel to the direction of acceleration
done
clear
D)
acceleration is zero
done
clear
E)
velocity is perpendicular to the direction of acceleration
done
clear
View Answer play_arrow
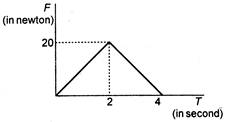
question_answer 51)
A body is initially at rest on a smooth surface. A force F, whose time variation is shown in the adjacent figure acts on it for a duration of 4 s. The momentum of the ball at the end of the 4 s is (in N-s):
A)
10
done
clear
B)
20
done
clear
C)
30
done
clear
D)
40
done
clear
E)
50
done
clear
View Answer play_arrow
question_answer 52) Two satellites P and Q are in the same circular orbit round the earth. The mass of P is greater than that of Q. It follows that:
A)
the speed of P is equal to that of Q
done
clear
B)
the speed of P is greater than that of Q
done
clear
C)
the speed of P is less than that of Q
done
clear
D)
the kinetic energy of P is equal to that of Q
done
clear
E)
the potential energy of P is equal to that of Q, taking the potential energy of a body to be zero at infinity
done
clear
View Answer play_arrow
question_answer 53) A particle is moving, eastwards with a velocity of 5 m/s. In 10 s, its velocity changes to 5 m/s northwards. The average acceleration in this time is:
A)
zero
done
clear
B)
\[\frac{1}{\sqrt{2}}m/{{s}^{2}}\]towards north-west
done
clear
C)
\[\frac{1}{\sqrt{2}}m/{{s}^{2}}\]towards north-east
done
clear
D)
\[\frac{1}{2}m/{{s}^{2}}\]towards north-west
done
clear
E)
\[\frac{1}{2}m/{{s}^{2}}\]towards north
done
clear
View Answer play_arrow
question_answer 54) A particle moving in one dimension with a constant acceleration of\[2\text{ }m/{{s}^{2}}\]is observed to cover a distance of 5m during a particular interval of Is. The distance covered by the particle in the next 1 s interval is (in metre):
A)
5
done
clear
B)
6
done
clear
C)
7
done
clear
D)
10
done
clear
E)
2
done
clear
View Answer play_arrow
question_answer 55) A body at rest is moved along a straight line by a machine which delivers constant power. The distance moved by the body in time t is proportional to:
A)
\[{{t}^{1/2}}\]
done
clear
B)
\[{{t}^{3/4}}\]
done
clear
C)
\[t\]
done
clear
D)
\[{{t}^{3/2}}\]
done
clear
E)
\[{{t}^{2}}\]
done
clear
View Answer play_arrow
question_answer 56) Two bodies, A and B initially, at rest, move towards each other under mutual force of attraction. At the instant when the speed of A is v and that of B is 2v, the speed of the centre of mass of the bodies is:
A)
3v
done
clear
B)
2v
done
clear
C)
1.5 v
done
clear
D)
v
done
clear
E)
zero
done
clear
View Answer play_arrow
question_answer 57) A mass 3m, initially at rest at the origin, explodes into three fragments of equal mass. Two of the fragments have speed v each and move perpendicular to each other. The third fragment will move with a speed:
A)
\[v/\sqrt{2}\]
done
clear
B)
\[v/2\]
done
clear
C)
\[v\]
done
clear
D)
\[\sqrt{2v}\]
done
clear
E)
\[2v\]
done
clear
View Answer play_arrow
question_answer 58) A constant force F is-pushing a 5 kg mass on a horizontal surface at a constant velocity of 2 m/s. The coefficient of friction between the surface and the mass is 0.3 (Take\[g=10\text{ }m/{{s}^{2}}\]). If F acts along the direction of motion, the rate at which F is doing work (in watt):
A)
3
done
clear
B)
6
done
clear
C)
10
done
clear
D)
15
done
clear
E)
30
done
clear
View Answer play_arrow
question_answer 59) The moment of inertia of a ring about of one its diameter is\[I\]. What will be its moment of inertia about a tangent parallel to the diameter?
A)
\[4I\]
done
clear
B)
\[2I\]
done
clear
C)
\[\frac{3}{2}I\]
done
clear
D)
\[3I\]
done
clear
E)
\[I\]
done
clear
View Answer play_arrow
question_answer 60) A massless spring of natural length of 0.5 m and spring constant 50 N/m has one end fixed and the other end attached to a mass of 250 g. The spring mass system is on a smooth floor. The mass is pulled until the length of the spring is 0.6 and then released from rest. The kinetic energy of the mass when the length of the spring is 0.5 m is:
A)
0.25 J
done
clear
B)
2.25 J
done
clear
C)
6.25 J
done
clear
D)
9 J
done
clear
E)
25 J
done
clear
View Answer play_arrow
question_answer 61) A disc, initially at rest, starts rotating about its own axis, with a constant angular acceleration of\[0.2\text{ }rad/{{s}^{2}}\]. The time taken by the disc to rotate by 10 rad is (in seconds):
A)
7.07
done
clear
B)
10
done
clear
C)
14.14
done
clear
D)
100
done
clear
E)
200
done
clear
View Answer play_arrow
question_answer 62) A thin disc is rotating with a constant angular velocity about its own axis. A is a point on the rim of the disc and B is a point half-way between the rim and the centre. The ratio of the velocity at A to that at B is:
A)
\[1:4\]
done
clear
B)
\[1:2\]
done
clear
C)
\[1:1\]
done
clear
D)
\[2:1\]
done
clear
E)
\[4:1\]
done
clear
View Answer play_arrow
question_answer 63) A simple pendulum has a time period of 1 s. In order to increase the time period to 2 s:
A)
the mass of the bob should be doubled
done
clear
B)
the length of the pendulum should be doubled
done
clear
C)
the length of the pendulum should be increased by a factor of 4
done
clear
D)
the length of the pendulum should be decreased a factor of 4
done
clear
E)
both the mass and the length of the pendulum should be doubled
done
clear
View Answer play_arrow
question_answer 64) The amplitude of a particle executing simple harmonic motion with a frequency of 60 Hz is 0.01 m. The maximum value of acceleration of the particle is:
A)
\[144{{\pi }^{2}}m/{{s}^{2}}\]
done
clear
B)
\[12m/{{s}^{2}}\]
done
clear
C)
\[11m/{{s}^{2}}\]
done
clear
D)
\[169m/{{s}^{2}}\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 65) Standing waves are formed on a string when interference occurs between two waves having:
A)
the same amplitude travelling in the same direction with no phase difference between them
done
clear
B)
the same amplitude, travelling in the opposite direction with no phase difference between them
done
clear
C)
different amplitudes travelling in the same direction
done
clear
D)
different amplitudes travelling in the opposite direction
done
clear
E)
the same amplitude travelling in the same direction with a phase difference of\[90{}^\circ \]
done
clear
View Answer play_arrow
question_answer 66) A 4 m long copper wire of cross-sectional area \[1.2c{{m}^{2}}\]is stretched by a force of\[4.8\times {{10}^{3}}N\]. Youngs modulus for copper\[(Y=1.2\times {{10}^{11}}N/{{m}^{2}})\]the increase in length of wire is:
A)
1.32 mm
done
clear
B)
0.8 mm
done
clear
C)
0.48 mm
done
clear
D)
5.36 mm
done
clear
E)
2.45 mm
done
clear
View Answer play_arrow
question_answer 67) A stationary police car sounds a siren with a frequency of 990 Hz. If the speed of sound is 330 m/s, an observer, driving towards the car with a speed of 33 m/s, will hear a frequency of:
A)
891 Hz
done
clear
B)
900 Hz
done
clear
C)
1089 Hz
done
clear
D)
1100 Hz
done
clear
E)
1210 Hz
done
clear
View Answer play_arrow
question_answer 68) The pressure required to stop the increase in volume of a copper block when it is heated from\[50{}^\circ C\]to\[70{}^\circ C\]. Coefficient of linear expansion of copper is\[8\times {{10}^{-6}}/{}^\circ C\]and bulk modulus of elasticity\[=3.6\times {{10}^{11}}N/{{m}^{2}},\]is:
A)
\[2.8\times {{10}^{5}}N/{{m}^{2}}\]
done
clear
B)
\[1.72\times {{10}^{8}}N/{{m}^{2}}\]
done
clear
C)
\[6.3\times {{10}^{3}}N/{{m}^{2}}\]
done
clear
D)
\[8\times {{10}^{-6}}N/{{m}^{2}}\]
done
clear
E)
\[1.57\times {{10}^{4}}N/{{m}^{2}}\]
done
clear
View Answer play_arrow
question_answer 69) Given that the surface tension of water is 75 dyne/cm, its density 1 g/cc and angle of contact zero, the height to which water rises in a capillary tube of 1 mm diameter is: (take\[g=10\text{ }m/{{s}^{2}}\])
A)
9.0 cm
done
clear
B)
7.5 cm
done
clear
C)
6.0 cm
done
clear
D)
3.0cm
done
clear
E)
1.5 cm
done
clear
View Answer play_arrow
question_answer 70) An open tank filled with water (density)\[\rho \]has a narrow hole at a depth of h below the water surface. The velocity of water flowing out is:
A)
\[hpg\]
done
clear
B)
\[2gh\]
done
clear
C)
\[\sqrt{2gh}\]
done
clear
D)
\[gh\]
done
clear
E)
\[\sqrt{2gh\rho }\]
done
clear
View Answer play_arrow
question_answer 71) A heat engine undergoes a process in which its internal energy decrease by 400 J and it gives out 150 J of heat. During the process:
A)
it does 250 J of work and its temperature rises
done
clear
B)
it does 250 J of work and its temperature falls
done
clear
C)
it does 550 J of work and its temperature rises
done
clear
D)
it does 550 J of work and its temperature falls
done
clear
E)
250 J of work is done on the system
done
clear
View Answer play_arrow
question_answer 72) An ideal gas heat engine operates in Carnot cycle between\[227{}^\circ C\]and\[127{}^\circ C\]. It absorbs \[6\times {{10}^{4}}\]cal of heat at higher temperature. Amount of heat converted into work, is:
A)
\[1.2\times {{10}^{4}}cal\]
done
clear
B)
\[2.4\times {{10}^{4}}cal\]
done
clear
C)
\[6.0\times {{10}^{4}}cal\]
done
clear
D)
\[4.8\times {{10}^{4}}cal\]
done
clear
E)
\[3.6\times {{10}^{4}}cal\]
done
clear
View Answer play_arrow
question_answer 73) An alkene \[{{C}_{4}}{{H}_{8}}\], was treated with ozone and then with zinc and water to give acetone and formaldehyde. The alkene is:
A)
propane
done
clear
B)
1-butene
done
clear
C)
2-methyl-2-butene
done
clear
D)
2-methyl propene
done
clear
E)
2-methyl butene
done
clear
View Answer play_arrow
question_answer 74) Sangers reagent is used for the identification of:
A)
N-terminal of peptide chain
done
clear
B)
C-terminal of a peptide chain
done
clear
C)
side chain of the amino acids
done
clear
D)
molecular weight of the peptide chain
done
clear
E)
number of amino acids in peptide chain
done
clear
View Answer play_arrow
question_answer 75) An alkane\[{{C}_{7}}{{H}_{16}}\]is produced by the reaction of lithium dipentyl cuparate with ethyl bromide. The structural formula of the product is:
A)
3-ethyl pentane
done
clear
B)
2-ethyl pentane
done
clear
C)
3-methyl hexane
done
clear
D)
2-methyl hexane
done
clear
E)
n-heptane
done
clear
View Answer play_arrow
question_answer 76) Which of the following compound is found most abundantly in nature?
A)
Fructose
done
clear
B)
Glucose
done
clear
C)
Starch
done
clear
D)
Cellulose
done
clear
E)
Maltose
done
clear
View Answer play_arrow
question_answer 77) Gabriel synthesis is used for the synthesis of:
A)
primary amines
done
clear
B)
secondary amines
done
clear
C)
aldehydes
done
clear
D)
acids
done
clear
E)
tertiary amines
done
clear
View Answer play_arrow
question_answer 78) Glycerol is:
A)
1, 3-dihydroxy propane
done
clear
B)
2, 3-dihydroxy propanone
done
clear
C)
2, 3-dihydroxy propane
done
clear
D)
1, 2, 3, 4-tetrahydroxy butane
done
clear
E)
1, 2, 3-propane triol
done
clear
View Answer play_arrow
question_answer 79) Propanal on reaction with dilute sodium hydroxide forms:
A)
\[C{{H}_{3}}C{{H}_{2}}C{{H}_{2}}C{{H}_{2}}C{{H}_{2}}CHO\]
done
clear
B)
\[C{{H}_{3}}C{{H}_{2}}CH(OH)C{{H}_{2}}C{{H}_{2}}CHO\]
done
clear
C)
\[C{{H}_{3}}C{{H}_{2}}C{{H}_{2}}CH(OH)C{{H}_{2}}CHO\]
done
clear
D)
\[C{{H}_{3}}C{{H}_{2}}CH(OH)CH(C{{H}_{3}})CHO\]
done
clear
E)
\[C{{H}_{3}}C{{H}_{2}}COOH\]
done
clear
View Answer play_arrow
question_answer 80) Complete combustion of 0.858 g of compound\[X\]gives 2.63 g of\[C{{O}_{2}}\]and 1.28 g of\[{{H}_{2}}O\]. The lowest molecular weight which\[X\]can have, is:
A)
43 g
done
clear
B)
86 g
done
clear
C)
129 g
done
clear
D)
172 g
done
clear
E)
22 g
done
clear
View Answer play_arrow
question_answer 81) What structural feature distinguishes glycine from other natural \[\alpha \]-aminoacids?
A)
It is optically inactive
done
clear
B)
It contains aromatic group
done
clear
C)
It is a dicarboxylic acid
done
clear
D)
It has a secondary amine
done
clear
E)
It contains two amino groups
done
clear
View Answer play_arrow
question_answer 82) Soft drink and baby feeding bottles are generally made up of:
A)
polyester
done
clear
B)
polyurethane
done
clear
C)
polyurea
done
clear
D)
polyamide
done
clear
E)
polystyrene
done
clear
View Answer play_arrow
question_answer 83) The product formed in the following reaction is: \[C{{H}_{3}}CH(C{{H}_{3}})CH=C{{H}_{2}}+HBr\] \[\xrightarrow{{}}product:\]
A)
\[{{(C{{H}_{3}})}_{2}}CHCH(Br)C{{H}_{3}}\]
done
clear
B)
\[{{(C{{H}_{3}})}_{2}}CHC{{H}_{2}}C{{H}_{2}}Br\]
done
clear
C)
\[{{(C{{H}_{3}})}_{2}}C(Br)C{{H}_{2}}C{{H}_{3}}\]
done
clear
D)
\[C{{H}_{3}}CH(C{{H}_{3}})CH(Br)C{{H}_{2}}C{{H}_{3}}\]
done
clear
E)
\[C{{H}_{3}}CH(C{{H}_{3}})CH(Br)C{{H}_{2}}(Br)\]
done
clear
View Answer play_arrow
question_answer 84) How many isomers can\[{{C}_{5}}{{H}_{12}}\]have?
A)
3
done
clear
B)
2
done
clear
C)
4
done
clear
D)
5
done
clear
E)
1
done
clear
View Answer play_arrow
question_answer 85) Which amino acid is achiral?
A)
Alanine
done
clear
B)
Valine
done
clear
C)
Proline
done
clear
D)
Histadine
done
clear
E)
Glycine
done
clear
View Answer play_arrow
question_answer 86) When propyne is treated with dilute sulphuric acid in presence of mercury (II) sulphate, the major product is:
A)
acetone
done
clear
B)
propene
done
clear
C)
propanol
done
clear
D)
propanal
done
clear
E)
2-propanol
done
clear
View Answer play_arrow
question_answer 87) Reduction of carbonyl compounds with hydrazine in presence of strong base is called:
A)
Cannizaros reaction
done
clear
B)
Clemmensens reduction
done
clear
C)
Wolff-Kishner reduction
done
clear
D)
Meerwein-Pondorf reduction
done
clear
E)
Beckmann rearrangement
done
clear
View Answer play_arrow
question_answer 88) Which of the following is the most stable form of cyclohexane?
A)
Boat
done
clear
B)
Planar
done
clear
C)
Twist boat
done
clear
D)
Half chair
done
clear
E)
Chair
done
clear
View Answer play_arrow
question_answer 89) What kind of bonding is responsible for the secondary structure of proteins?
A)
Covalent bonding
done
clear
B)
Hydrogen bonding
done
clear
C)
Ionic bonding
done
clear
D)
van der Waals forces
done
clear
E)
Amino acid sequence
done
clear
View Answer play_arrow
question_answer 90) The beta and alpha glucose have different specific rotations. When either is dissolved in water, their rotation changes until the same fixed value results. This is called:
A)
epimerization
done
clear
B)
racemization
done
clear
C)
anomerization
done
clear
D)
mutarotation
done
clear
E)
inversion
done
clear
View Answer play_arrow
question_answer 91)
The product of following reaction is:
A)
pentanol
done
clear
B)
2-pentanol
done
clear
C)
pentane
done
clear
D)
1, 2-pentan-di-ol
done
clear
E)
pent-2-one
done
clear
View Answer play_arrow
question_answer 92) Streptomycin is used as:
A)
antipyretic
done
clear
B)
mordant
done
clear
C)
antibiotic
done
clear
D)
antihistamine
done
clear
E)
hypnotics
done
clear
View Answer play_arrow
question_answer 93) Which one of the following will be most basic?
A)
Aniline
done
clear
B)
p -methoxyaniline
done
clear
C)
p-nitroaniime
done
clear
D)
p -methylaniline
done
clear
E)
Benzylamine
done
clear
View Answer play_arrow
question_answer 94) Which of the following will exhibit highest boiling point?
A)
\[C{{H}_{3}}C{{H}_{2}}OC{{H}_{2}}C{{H}_{3}}\]
done
clear
B)
\[C{{H}_{3}}C{{H}_{2}}C{{H}_{2}}C{{H}_{2}}C{{H}_{2}}OH\]
done
clear
C)
\[C{{H}_{3}}C{{H}_{2}}C{{H}_{2}}CH(C{{H}_{3}})OH\]
done
clear
D)
\[C{{H}_{3}}C{{H}_{2}}C{{(C{{H}_{3}})}_{2}}OH\]
done
clear
E)
\[C{{H}_{3}}C{{(C{{H}_{3}})}_{2}}C{{H}_{2}}H\]
done
clear
View Answer play_arrow
question_answer 95) Geometrical isomerism is possible in case of:
A)
2-butyne
done
clear
B)
1-butene
done
clear
C)
propene
done
clear
D)
2-butene
done
clear
E)
pentene
done
clear
View Answer play_arrow
question_answer 96) n-butyl benzene on oxidation will give:
A)
benzoic acid
done
clear
B)
butanoic acid
done
clear
C)
benzyl alcohol
done
clear
D)
benzaldehyde
done
clear
E)
4-phenyl butanoic acid
done
clear
View Answer play_arrow
question_answer 97) The element with electronic configuration of its atom\[1{{s}^{2}},2{{s}^{2}},2{{p}^{6}},3{{s}^{2}},3{{p}^{6}},3{{d}^{10}},4{{s}^{1}}\]is:
A)
\[Fe\]
done
clear
B)
\[Co\]
done
clear
C)
\[Ni\]
done
clear
D)
\[Zn\]
done
clear
E)
\[Cu\]
done
clear
View Answer play_arrow
question_answer 98) According to Bohrs theory the energy required for the transition of H atom from \[n=6\]to\[n=8\]state is:
A)
equal to the energy required for the transition from\[n=5\]to\[n=7\]state
done
clear
B)
larger than in A
done
clear
C)
less than in A
done
clear
D)
equal to the energy required for the transition from n = 7 to n = 9 state
done
clear
E)
less than D
done
clear
View Answer play_arrow
question_answer 99) The dimensions of viscosity coefficient are:
A)
\[M{{L}^{-1}}{{T}^{-1}}\]
done
clear
B)
\[ML{{T}^{-1}}\]
done
clear
C)
\[M{{L}^{-1}}T\]
done
clear
D)
\[MLT\]
done
clear
E)
\[ML{{T}^{-2}}\]
done
clear
View Answer play_arrow
question_answer 100) In the chemical reaction\[2S{{O}_{2}}+{{O}_{2}}\xrightarrow{{}}2S{{O}_{3}}\]increasing the total pressure leads to:
A)
increase in amount of\[S{{O}_{3}}\]
done
clear
B)
increase in partial pressure of\[{{O}_{2}}\]
done
clear
C)
increase in the partial pressure of\[S{{O}_{2}}\]
done
clear
D)
change in equilibrium constant
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 101) A 4p-orbital has:
A)
one node
done
clear
B)
two nodes
done
clear
C)
three nodes
done
clear
D)
four nodes
done
clear
E)
five nodes
done
clear
View Answer play_arrow
question_answer 102) At the triple point of water the number of phases in equilibrium are:
A)
zero
done
clear
B)
one
done
clear
C)
two
done
clear
D)
three
done
clear
E)
four
done
clear
View Answer play_arrow
question_answer 103) The emf of a Daniell cell at 298 K is\[{{E}_{1}}\] \[Zn/ZnS{{O}_{4}}(0.01\text{ }M)||CuS{{O}_{4}}\text{(1}\text{.0}\,\text{M) }\!\!|\!\!\text{ }Cu\] When the concentration of\[ZnS{{O}_{4}}\]is 1.0 M and that of\[CuS{{O}_{4}}\]is 0.01 M. The emf changed to \[{{E}_{2}}\]. What is the relation between\[{{E}_{1}}\]and\[{{E}_{2}}\]?
A)
\[{{E}_{1}}={{E}_{2}}\]
done
clear
B)
\[{{E}_{2}}=0\ne {{E}_{1}}\]
done
clear
C)
\[{{E}_{1}}>{{E}_{2}}\]
done
clear
D)
\[{{E}_{1}}<{{E}_{2}}\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 104) The correct order of ionization energies is:
A)
\[Zn<Cd<Hg\]
done
clear
B)
\[Na<Rb<Cs\]
done
clear
C)
\[Rb<Cs<Na\]
done
clear
D)
\[Na<Cs<Rb\]
done
clear
E)
\[Cs<Rb<Na\]
done
clear
View Answer play_arrow
question_answer 105) The structure of\[C{{H}_{2}}=C{{H}_{2}}\]is:
A)
linear
done
clear
B)
planar
done
clear
C)
non-planar
done
clear
D)
has resonance structure
done
clear
E)
square planar
done
clear
View Answer play_arrow
question_answer 106) The hybridization of xenon in\[Xe{{F}_{2}}\]is:
A)
\[s{{p}^{3}}\]
done
clear
B)
\[s{{p}^{2}}\]
done
clear
C)
\[s{{p}^{3}}d\]
done
clear
D)
\[s{{p}^{2}}d\]
done
clear
E)
\[s{{p}^{3}}{{d}^{2}}\]
done
clear
View Answer play_arrow
question_answer 107) The reagent commonly used to determine hardness of water titrimetrically is:
A)
oxalic acid
done
clear
B)
sodium citrate
done
clear
C)
disodium salt of EDTA
done
clear
D)
sodium carbonate
done
clear
E)
sodium thiosulphate
done
clear
View Answer play_arrow
question_answer 108) 0.01 M solution of\[KCl\]and\[BaC{{l}_{2}}\]are prepared in water. The freezing points of \[KCl\]is found to be\[-2{}^\circ C\]. What is the freezing point of \[BaC{{l}_{2}}\] solution assuming both\[KCl\] and\[BaC{{l}_{2}}\]to be completely ionized?
A)
\[-3{}^\circ C\]
done
clear
B)
\[+3{}^\circ C\]
done
clear
C)
\[-2{}^\circ C\]
done
clear
D)
\[-4{}^\circ C\]
done
clear
E)
\[5{}^\circ C\]
done
clear
View Answer play_arrow
question_answer 109) 45 g of ethylene glycol is mixed with 600 g of water. What is the freezing point of the solution? \[({{k}_{f}}=1.86\text{ }K\text{ }kg\text{ }mo{{l}^{-1}})\]
A)
\[-270.90\text{ }K\]
done
clear
B)
\[270.90\text{ }K\]
done
clear
C)
\[273\text{ }K\]
done
clear
D)
\[274.15\text{ }K\]
done
clear
E)
\[-\text{ }274.15\text{ }K\]
done
clear
View Answer play_arrow
question_answer 110) Which of the following is used as a preservative for biological specimens?
A)
Acetic acid
done
clear
B)
Chloroform
done
clear
C)
Formalin
done
clear
D)
Formic acid
done
clear
E)
Acetone
done
clear
View Answer play_arrow
question_answer 111) The charge required to deposit 9 g of\[Al\]from an\[A{{l}^{3+}}\]solution is:
A)
32166.3 C
done
clear
B)
96500 C
done
clear
C)
3216.33 C
done
clear
D)
9650 C
done
clear
E)
\[8.685\times {{10}^{5}}C\]
done
clear
View Answer play_arrow
question_answer 112) A compound formed by elements A and B crystallizes in the cubic arrangement in which A atoms are at the corners of a cube and B atoms are at the face centres. What is the formula of compound?
A)
\[A{{B}_{3}}\]
done
clear
B)
\[B{{ }_{3}}A\]
done
clear
C)
\[{{A}_{2}}{{B}_{2}}\]
done
clear
D)
\[A{{B}_{2}}\]
done
clear
E)
\[A{{B}_{4}}\]
done
clear
View Answer play_arrow
question_answer 113) What is the pH value of\[M\,{{H}_{2}}S{{O}_{4}}\]?
A)
Zero
done
clear
B)
One
done
clear
C)
2
done
clear
D)
0.3010
done
clear
E)
\[-0.3010\]
done
clear
View Answer play_arrow
question_answer 114) \[{{F}_{2}}C=C{{F}_{2}}\]is a monomer of:
A)
glyptal
done
clear
B)
Teflon
done
clear
C)
orlon
done
clear
D)
buna-S
done
clear
E)
rubber
done
clear
View Answer play_arrow
question_answer 115) To an\[A{{g}_{2}}Cr{{O}_{4}}\]solution over its own precipitate, \[CrO_{4}^{2-}\]ions are added. This results in:
A)
increase in\[A{{g}^{+}}\]concentration
done
clear
B)
decrease in concentration
done
clear
C)
increase in the solubility product
done
clear
D)
decrease in the solubility product
done
clear
E)
\[A{{g}^{+}}\]goes into solution from the precipitate
done
clear
View Answer play_arrow
question_answer 116) For a first order reaction, to obtain a positive slope, we need to plot {[A] is the concentration of reactant A}:
A)
\[{{\log }_{10}}[A]\,vs\,t\]
done
clear
B)
\[-{{\log }_{e}}[A]\,vs\,t\]
done
clear
C)
\[{{\log }_{10}}[A]\,vs\,\log t\]
done
clear
D)
\[[A]\,vs\,t\]
done
clear
E)
\[[A]\,vs\,\log t\]
done
clear
View Answer play_arrow
question_answer 117) The species A in the reaction is \[_{92}{{U}^{236}}{{\xrightarrow{{}}}_{54}}{{X}^{144}}{{+}_{38}}S{{r}^{90}}+A:\]
A)
\[_{1}{{H}^{1}}\]
done
clear
B)
\[_{0}{{n}^{1}}\]
done
clear
C)
\[_{0}{{n}^{1}}\]
done
clear
D)
\[{{2}_{1}}{{H}^{1}}\]
done
clear
E)
\[{{2}_{0}}{{n}^{1}}\]
done
clear
View Answer play_arrow
question_answer 118) In Brownian movement or motion, the paths of the particles are:
A)
linear
done
clear
B)
zig-zag
done
clear
C)
uncertain
done
clear
D)
curved
done
clear
E)
oscillatory
done
clear
View Answer play_arrow
question_answer 119) The heats of adsorption in physisorption (or physical adsorption) lie in the range of (in kJ/mol):
A)
40-400
done
clear
B)
40-100
done
clear
C)
10-40
done
clear
D)
200-400
done
clear
E)
1-10
done
clear
View Answer play_arrow
question_answer 120) The reaction\[2{{H}_{2}}{{O}_{2}}\xrightarrow{{}}2{{H}_{2}}O+{{O}_{2}}\]is:
A)
a redox reaction
done
clear
B)
a hydrolysis reaction
done
clear
C)
a solvolysis reaction
done
clear
D)
an oscillatory reaction
done
clear
E)
disproportionation
done
clear
View Answer play_arrow
question_answer 121) The most abundant element in the earths crust (by weight) is:
A)
\[Si\]
done
clear
B)
\[Al\]
done
clear
C)
\[O\]
done
clear
D)
\[Fe\]
done
clear
E)
\[Na\]
done
clear
View Answer play_arrow
question_answer 122) The most electropositive metals are isolated from their ores by:
A)
high temperature reduction with carbon
done
clear
B)
self-reduction
done
clear
C)
thermal decomposition
done
clear
D)
electrolysis of fused ionic salts
done
clear
E)
displacement method
done
clear
View Answer play_arrow
question_answer 123) The reaction of slaked lime with \[C{{l}_{2}}\] gas gives:
A)
only \[Ca{{(OCl)}_{2}}\]
done
clear
B)
only \[CaC{{l}_{2}}\]
done
clear
C)
a mixture of\[Ca{{(OCl)}_{2}},Ca{{(OH)}_{2}},CaC{{l}_{2}}\]and\[{{H}_{2}}O\]
done
clear
D)
quicklime
done
clear
E)
baryta water
done
clear
View Answer play_arrow
question_answer 124) The nitride salt of\[Ca\]when treated with\[{{H}_{2}}O\]gives:
A)
\[{{N}_{2}}\]
done
clear
B)
\[CaO\]
done
clear
C)
\[Ca{{H}_{2}}\]
done
clear
D)
\[N{{H}_{3}}\]
done
clear
E)
\[{{N}_{2}}{{H}_{4}}\]
done
clear
View Answer play_arrow
question_answer 125) Correct formula of the complex formed in the brown ring test for nitrates is:
A)
\[FeS{{O}_{4}}NO\]
done
clear
B)
\[{{[Fe{{({{H}_{2}}O)}_{5}}NO]}^{2+}}\]
done
clear
C)
\[{{[Fe{{({{H}_{2}}O)}_{5}}NO]}^{+}}\]
done
clear
D)
\[{{[Fe{{({{H}_{2}}O)}_{5}}NO]}^{3}}\]
done
clear
E)
\[Fe{{({{H}_{2}}O)}_{4}}{{(NO)}_{2}}]\]
done
clear
View Answer play_arrow
question_answer 126) \[AgCl\] is soluble in \[N{{H}_{4}}OH\] solution. The solubility is due to formation of:
A)
\[AgOH\]
done
clear
B)
\[A{{g}_{2}}O\]
done
clear
C)
\[{{[Ag{{(N{{H}_{3}})}_{2}}]}^{+}}\]
done
clear
D)
\[N{{H}_{4}}Cl\]
done
clear
E)
\[[AgCl(N{{H}_{3}})]\]
done
clear
View Answer play_arrow
question_answer 127) \[{{O}_{3}}\]is used to purify water since:
A)
is paramagnetic
done
clear
B)
absorbs harmful UV radiation
done
clear
C)
is reducing
done
clear
D)
destroys bacteria and viruses
done
clear
E)
is allotrope of \[{{O}_{2}}\]
done
clear
View Answer play_arrow
question_answer 128) Producer gas is a mixture of:
A)
\[CO+{{H}_{2}}\]
done
clear
B)
\[{{H}_{2}}+C{{O}_{2}}\]
done
clear
C)
\[CO+{{N}_{2}}\]
done
clear
D)
\[C{{O}_{2}}+{{H}_{2}}\]
done
clear
E)
\[C{{O}_{4}}+{{H}_{2}}+{{O}_{2}}\]
done
clear
View Answer play_arrow
question_answer 129) The shape of gaseous\[SnC{{l}_{2}}\]is:
A)
tetrahedral
done
clear
B)
linear
done
clear
C)
angular
done
clear
D)
T-shaped
done
clear
E)
distorted tetrahedral
done
clear
View Answer play_arrow
question_answer 130) Galvanization of iron denotes coating with:
A)
\[Al\]
done
clear
B)
\[Sn\]
done
clear
C)
\[Cd\]
done
clear
D)
\[Pb\]
done
clear
E)
\[Zn\]
done
clear
View Answer play_arrow
question_answer 131) The three-dimensional lattice of zeolites consists of:
A)
\[{{[S{{i}_{2}}{{O}_{7}}]}^{6}}\]
done
clear
B)
\[[Si{{O}_{3}}]_{n}^{2n-}\]
done
clear
C)
\[[{{S}_{2}}{{O}_{5}}]_{n}^{2n-}\]
done
clear
D)
only\[Si{{O}_{2}}\]
done
clear
E)
\[{{[AlS{{i}_{3}}{{O}_{8}}]}^{-}}\]
done
clear
View Answer play_arrow
question_answer 132) Which one of the following is triple superphosphate?
A)
\[[C{{a}_{3}}{{(P{{O}_{4}})}_{2}}.Ca{{F}_{2}}]\]
done
clear
B)
\[Ca{{({{H}_{2}}P{{O}_{4}})}_{2}}+CaS{{O}_{4}}\]
done
clear
C)
\[Ca{{({{H}_{2}}P{{O}_{4}})}_{2}}\]
done
clear
D)
\[C{{a}_{3}}{{(P{{O}_{4}})}_{2}}\]
done
clear
E)
\[CaH{{P}_{4}}.2{{H}_{2}}O\]
done
clear
View Answer play_arrow
question_answer 133) The lowest boiling point of helium is due to its:
A)
inertness
done
clear
B)
gaseous nature
done
clear
C)
high Polaris ability
done
clear
D)
weak vander Weals forces between atoms
done
clear
E)
small size
done
clear
View Answer play_arrow
question_answer 134) Nickel is purified by thermal decomposition of its:
A)
hydride
done
clear
B)
chloride
done
clear
C)
azide
done
clear
D)
carbonyl
done
clear
E)
iodide
done
clear
View Answer play_arrow
question_answer 135) The number of isomers exhibited by\[[Cr{{(N{{H}_{3}})}_{3}}C{{l}_{3}}]\]is:
A)
2
done
clear
B)
3
done
clear
C)
4
done
clear
D)
5
done
clear
E)
6
done
clear
View Answer play_arrow
question_answer 136) Among lanthanide ions, the most stable +2 oxidation state is exhibited by:
A)
\[Ce\]
done
clear
B)
\[Eu\]
done
clear
C)
\[Sm\]
done
clear
D)
\[Nb\]
done
clear
E)
\[Gd\]
done
clear
View Answer play_arrow
question_answer 137) Of the following species, one Which can form transition metal organometallics is:
A)
\[C{{O}_{2}}\]
done
clear
B)
\[NO\]
done
clear
C)
\[CN\]
done
clear
D)
\[CO_{3}^{2-}\]
done
clear
E)
\[RNC\]
done
clear
View Answer play_arrow
question_answer 138) For the square planar complex \[[M(a)(b)(c)(d)]\] where, M= central metal a, b, c and d are monodentate ligands) the number of possible geometrical isomers are:
A)
1
done
clear
B)
2
done
clear
C)
3
done
clear
D)
4
done
clear
E)
6
done
clear
View Answer play_arrow
question_answer 139) Which of the following molecules can act as an oxidizing as well as a reducing agent?
A)
\[{{H}_{2}}S\]
done
clear
B)
\[S{{O}_{3}}\]
done
clear
C)
\[{{H}_{2}}{{O}_{2}}\]
done
clear
D)
\[{{F}_{2}}\]
done
clear
E)
\[{{H}_{2}}S{{O}_{4}}\]
done
clear
View Answer play_arrow
question_answer 140) Transition metals usually exhibit highest oxidation states in their:
A)
chlorides
done
clear
B)
fluorides
done
clear
C)
bromides
done
clear
D)
iodides
done
clear
E)
hydrides
done
clear
View Answer play_arrow
question_answer 141) The most stable +2 oxidation state is exhibited by:
A)
\[Fe\]
done
clear
B)
\[Sn\]
done
clear
C)
\[Pb\]
done
clear
D)
\[Si\]
done
clear
E)
\[Ge\]
done
clear
View Answer play_arrow
question_answer 142) Which of the following substances has the least ionic character?
A)
\[MgC{{l}_{2}}\]
done
clear
B)
\[AlC{{l}_{3}}\]
done
clear
C)
\[NaCl\]
done
clear
D)
\[LiCl\]
done
clear
E)
\[NaF\]
done
clear
View Answer play_arrow
question_answer 143) Which of the following molecules will have unequal bond lengths?
A)
\[N{{F}_{3}}\]
done
clear
B)
\[B{{F}_{3}}\]
done
clear
C)
\[P{{F}_{5}}\]
done
clear
D)
\[S{{F}_{6}}\]
done
clear
E)
\[Si{{F}_{4}}\]
done
clear
View Answer play_arrow
question_answer 144) Which one of the following elements is most reactive?
A)
\[He\]
done
clear
B)
\[Ne\]
done
clear
C)
\[Ar\]
done
clear
D)
\[Kr\]
done
clear
E)
\[Xe\]
done
clear
View Answer play_arrow
question_answer 145) Bakelite is obtained from phenol by reacting with:
A)
acetaldehyde
done
clear
B)
acetal
done
clear
C)
formaldehyde
done
clear
D)
chlorobenzene
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 146) What is the half-life of\[_{6}{{C}^{14}},\]disintegration constant is\[2.31\times {{10}^{-4}}y{{r}^{-1}}\]?
A)
\[0.3\times {{10}^{4}}yr\]
done
clear
B)
\[0.3\times {{10}^{3}}yr\]
done
clear
C)
\[0.3\times {{10}^{8}}yr\]
done
clear
D)
\[0.3\times {{10}^{2}}yr\]
done
clear
E)
\[0.3\times {{10}^{-4}}yr\]
done
clear
View Answer play_arrow
question_answer 147) Which of the following is isoelectronic with\[C{{O}_{2}}\]?
A)
\[N{{O}_{2}}\]
done
clear
B)
\[NO\]
done
clear
C)
\[{{N}_{2}}O\]
done
clear
D)
\[{{N}_{2}}{{O}_{4}}\]
done
clear
E)
\[{{N}_{2}}{{O}_{5}}\]
done
clear
View Answer play_arrow
question_answer 148) The heat of combustion of carbon monoxide at\[27{}^\circ C\]will differ from one another by:
A)
27cal
done
clear
B)
54 cal
done
clear
C)
300 cal
done
clear
D)
600 cal
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 149) During electrolysis of water the volume of\[{{O}_{2}}\]liberated is\[2.24\,d{{m}^{3}}\]. The volume of hydrogen liberated, under same conditions will be:
A)
\[2.24\,d{{m}^{3}}\]
done
clear
B)
\[1.12\,d{{m}^{3}}\]
done
clear
C)
\[4.48\text{ }d{{m}^{3}}\]
done
clear
D)
\[0.56\text{ }d{{m}^{3}}\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 150) What is the frequency of a X-ray photon whose momentum is\[1.1\times {{10}^{-23}}kg\text{ }m{{s}^{-2}}\]?
A)
\[5\times {{10}^{16}}Hz\]
done
clear
B)
\[5\times {{10}^{17}}Hz\]
done
clear
C)
\[0.5\times {{10}^{18}}Hz\]
done
clear
D)
\[5\times {{10}^{18}}Hz\]
done
clear
E)
\[5\times {{10}^{-16}}Hz\]
done
clear
View Answer play_arrow
question_answer 151) The oxidation states of iodine in\[HI{{O}_{4}},{{H}_{3}}I{{O}_{5}}\]and\[{{H}_{5}}I{{O}_{6}}\]are respectively:
A)
\[+1,+3,+7\]
done
clear
B)
\[+7,+7,+3\]
done
clear
C)
\[+7,+7,+7\]
done
clear
D)
\[+7,+5,+3\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 152) The elements commonly used for making transistors are:
A)
C and Si
done
clear
B)
Ga and In
done
clear
C)
P and As
done
clear
D)
Si and Ge
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 153) Alcoholic beverages contain:
A)
isopropyl alcohol
done
clear
B)
n-propyl alcohol
done
clear
C)
ethyl alcohol
done
clear
D)
methyl alcohol
done
clear
E)
isobutyl alcohol
done
clear
View Answer play_arrow
question_answer 154) The enzymes which are used to convert starch into ethyl alcohol are:
A)
maltase, diastase
done
clear
B)
diastase, maltase, zymase
done
clear
C)
invertase, zymase
done
clear
D)
invertase, diastase, maltase
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 155) The acid which contains the aldehyde group is:
A)
acetic acid
done
clear
B)
formic acid
done
clear
C)
benzoic acid
done
clear
D)
propionic acid
done
clear
E)
picric acid
done
clear
View Answer play_arrow
question_answer 156) Vinegar is a solution of acetic acid which is:
A)
15-20%
done
clear
B)
20-25%
done
clear
C)
6-8%
done
clear
D)
2-4%
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 157) In the reaction: \[C{{H}_{3}}OH\xrightarrow[{}]{oxidation}A\xrightarrow[{}]{N{{H}_{3}}}B;\]A and B are:
A)
\[HCHO,\text{ }HCOON{{H}_{4}}\]
done
clear
B)
\[HCOOH,HCOON{{H}_{4}}\]
done
clear
C)
\[HCOOH,HCON{{H}_{2}}\]
done
clear
D)
\[HCHO\text{ },\text{ }HCON{{H}_{2}}\]
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 158) Which of the following ligands is not a chelating agent?
A)
EDTA
done
clear
B)
en
done
clear
C)
Oxalate
done
clear
D)
Pyridine
done
clear
E)
None of these
done
clear
View Answer play_arrow
question_answer 159) Pyrolusite is an ore of:
A)
magnesium
done
clear
B)
manganese
done
clear
C)
zinc
done
clear
D)
iron
done
clear
E)
copper
done
clear
View Answer play_arrow
question_answer 160) The human body does not produce:
A)
enzymes
done
clear
B)
vitamins
done
clear
C)
proteins
done
clear
D)
nucleic acids
done
clear
E)
all of these
done
clear
View Answer play_arrow
question_answer 161) A solid AB has\[NaCl\]structure. If the radius of cation\[{{A}^{+}}\]is 170 pm. Calculate the maximum possible radius of the anion\[{{B}^{-}}\].
A)
210.3pm
done
clear
B)
397.4pm
done
clear
C)
410.6pm
done
clear
D)
347.9pm
done
clear
E)
156.3 pm
done
clear
View Answer play_arrow
question_answer 162) Sea weeds are an important source of:
A)
chlorine
done
clear
B)
bromine
done
clear
C)
iodine
done
clear
D)
zinc
done
clear
E)
fluorine
done
clear
View Answer play_arrow
question_answer 163) The mass of 1 mole of electrons is:
A)
\[9.1\times {{10}^{-28}}g\]
done
clear
B)
1.008 mg
done
clear
C)
0.55 mg
done
clear
D)
\[9.1\times {{10}^{-27}}mg\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 164) Which one of the following is an ester?
A)
Coconut oil
done
clear
B)
Kerosene oil
done
clear
C)
Soap
done
clear
D)
Glycerine
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 165) Green vitriol is:
A)
\[FeS{{O}_{4}}.7{{H}_{2}}O\]
done
clear
B)
\[ZnS{{O}_{4}}.7{{H}_{2}}O\]
done
clear
C)
\[CuS{{O}_{4}}.5{{H}_{2}}O\]
done
clear
D)
\[CaS{{O}_{4}}.\frac{1}{2}{{H}_{2}}O\]
done
clear
E)
\[MgS{{O}_{4}}.7{{H}_{2}}O\]
done
clear
View Answer play_arrow
question_answer 166) Mixture of\[MgC{{l}_{2}}\]and\[MgO\]is called:
A)
portland cement
done
clear
B)
sorrels cement
done
clear
C)
double salt
done
clear
D)
gypsum
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 167) Bronze is a mixture of:
A)
\[Pb+Sn\]
done
clear
B)
\[Cu+Sn\]
done
clear
C)
\[Cu+Zn\]
done
clear
D)
\[Pb+Zn\]
done
clear
E)
\[Al+Ni\]
done
clear
View Answer play_arrow
question_answer 168) LPG mainly contains:
A)
ethyne
done
clear
B)
butane
done
clear
C)
methane
done
clear
D)
ethane
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 169) Equal moles of water and urea are taken in a flask. What is mass percentage of urea in the solution?
A)
23.077%
done
clear
B)
30.77%
done
clear
C)
2.3077%
done
clear
D)
0.23077%
done
clear
E)
46.154%
done
clear
View Answer play_arrow
question_answer 170) The radiant energy from the sun is due to:
A)
combustion
done
clear
B)
nuckar fusion
done
clear
C)
nuclear fission
done
clear
D)
chemical reaction
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 171) The co-ordination number of platinum in the complex\[[Pt{{(N{{H}_{3}})}_{4}}C{{l}_{2}}]\]is:
A)
2
done
clear
B)
4
done
clear
C)
6
done
clear
D)
8
done
clear
E)
5
done
clear
View Answer play_arrow
question_answer 172) Average speed\[{{C}_{av}}\]is:
A)
\[\sqrt{2}\,kT/m\]
done
clear
B)
\[\sqrt{8}\,kT/\pi m\]
done
clear
C)
\[\sqrt{3}\,kT/m\]
done
clear
D)
\[\sqrt{3}\,kT/m\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 173) 10g concentrated solution of\[CuS{{O}_{4}}\]is electrolysed passing 0.01 F of electricity. The volume of oxygen liberated at anode of STP is:
A)
22.4 L
done
clear
B)
11.2L
done
clear
C)
5.6 L
done
clear
D)
0.056 L
done
clear
E)
44.8 L
done
clear
View Answer play_arrow
question_answer 174) Which of the following unit cell having maximum number of atoms?
A)
BCC
done
clear
B)
HCP
done
clear
C)
FCC
done
clear
D)
Cubic
done
clear
E)
None of these
done
clear
View Answer play_arrow
question_answer 175) Sulphur colloid prepared by:
A)
mechanical dispersion
done
clear
B)
oxidation
done
clear
C)
electrical dispersion
done
clear
D)
reduction
done
clear
E)
dialysis
done
clear
View Answer play_arrow
question_answer 176) Reduction potentials of A, B, C and D are 0.8 V, 0.79 V, 0.34 V and\[-2.37\text{ }V\]respectively. Which element displaces all the other three elements?
A)
B
done
clear
B)
A
done
clear
C)
D
done
clear
D)
C
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 177) In an isothermal process:
A)
\[q=0\]and \[\Delta E=0\]
done
clear
B)
\[q\ne 0\]and \[\Delta E=0\]
done
clear
C)
\[q=0\]and \[\Delta E\ne 0\]
done
clear
D)
\[q\ne 0\]and \[\Delta E\ne 0\]
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 178) A 5 molar solution of \[{{H}_{2}}S{{O}_{4}}\] is diluted from 1 L to 10 L. What is the normality of the solution?
A)
0.25 N
done
clear
B)
1 N
done
clear
C)
2N
done
clear
D)
7 N
done
clear
E)
5N
done
clear
View Answer play_arrow
question_answer 179) Vitamin\[{{B}_{12}}\]contains:
A)
\[Co\]
done
clear
B)
\[Mn\]
done
clear
C)
\[Mg\]
done
clear
D)
\[Fe\]
done
clear
E)
\[Cu\]
done
clear
View Answer play_arrow
question_answer 180) Fluorine with dilute\[NaOH\]give:
A)
\[O{{F}_{2}}\]
done
clear
B)
\[{{O}_{3}}\]
done
clear
C)
\[{{O}_{2}}\]
done
clear
D)
HF and\[{{O}_{2}}\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 181) \[Si-O\]bond can be broken by:
A)
\[HCl\]
done
clear
B)
\[Na\]
done
clear
C)
\[NaOH\]
done
clear
D)
\[HF\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 182) Which of the following does not contain silicon?
A)
Kaolin
done
clear
B)
Agate
done
clear
C)
Ruby
done
clear
D)
Quartz
done
clear
E)
both (c) and (d)
done
clear
View Answer play_arrow
question_answer 183) The oxidation number of nickel in the complex \[[Ni{{(CO)}_{4}}]\] is:
A)
4
done
clear
B)
2
done
clear
C)
zero
done
clear
D)
3
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 184) Hall and Heroults process is used for:
A)
extraction of\[Al\]
done
clear
B)
purification of \[A{{l}_{2}}{{O}_{3}}\]
done
clear
C)
refining of \[Al\]
done
clear
D)
extraction of\[Ag\]
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 185) The composition of common glass is:
A)
\[N{{a}_{2}}O.CaO.6Si{{O}_{2}}\]
done
clear
B)
\[N{{a}_{2}}O.A{{l}_{2}}{{O}_{3}}.2Si{{O}_{2}}\]
done
clear
C)
\[CaO.A{{l}_{2}}{{O}_{3}}.Si{{O}_{2}}\]
done
clear
D)
\[N{{a}_{2}}O.CaOA{{l}_{2}}{{O}_{3}}.6Si{{O}_{2}}\]
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 186) The substance used as an activator in froth floatation process is:
A)
potassium ethyl xanthate
done
clear
B)
sodium cyanide
done
clear
C)
copper sulphate
done
clear
D)
pine oil
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 187) EDTA is used for the estimation of:
A)
\[N{{a}^{+}}\]and\[{{K}^{+}}\]ions
done
clear
B)
\[C{{l}^{-}}\]and\[B{{r}^{-}}\]ions
done
clear
C)
\[C{{u}^{2+}}\]and\[A{{g}^{+}}\]ions
done
clear
D)
\[C{{a}^{2+}}\]and\[M{{g}^{2+}}\]ions
done
clear
E)
\[Ag\]and\[M{{g}^{2+}}\]ions
done
clear
View Answer play_arrow
question_answer 188) Chloretone is used as:
A)
anaesthetic
done
clear
B)
hypnotic
done
clear
C)
antibiotic
done
clear
D)
antiseptic
done
clear
E)
sedative
done
clear
View Answer play_arrow
question_answer 189) Solution of\[AlC{{l}_{3}}\]in water is:
A)
acidic
done
clear
B)
basic
done
clear
C)
neutral
done
clear
D)
amphoteric
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 190) An aqueous solution of glucose is 20% in strength. The volume in which 1g-mole of it is dissolved will be:
A)
9 L
done
clear
B)
1.8 L
done
clear
C)
8 L
done
clear
D)
0.9 L
done
clear
E)
10 L
done
clear
View Answer play_arrow
question_answer 191) Amphoteric oxide combination are in:
A)
\[ZnO,{{K}_{2}}O,S{{O}_{3}}\]
done
clear
B)
\[ZnO,{{P}_{2}}{{O}_{5}},C{{l}_{2}}{{O}_{7}}\]
done
clear
C)
\[Sn{{O}_{2}},A{{l}_{2}}{{O}_{3}},ZnO\]
done
clear
D)
\[Pb{{O}_{2}},Sn{{O}_{2}},S{{O}_{3}}\]
done
clear
E)
None of the above
done
clear
View Answer play_arrow
question_answer 192) Which is a natural polymer?
A)
Cellulose
done
clear
B)
PVC
done
clear
C)
Teflon
done
clear
D)
SBR
done
clear
E)
Nylon-6
done
clear
View Answer play_arrow
question_answer 193) The equation of the base BC of an equilateral triangle ABC is\[x+y=2\]and A is\[(2,-1)\]. The length of the side of the triangle is:
A)
\[\sqrt{2}\]
done
clear
B)
\[{{\left( \frac{3}{2} \right)}^{\frac{1}{2}}}\]
done
clear
C)
\[{{\left( \frac{1}{2} \right)}^{\frac{1}{2}}}\]
done
clear
D)
\[\left( \frac{1}{\sqrt{2}} \right)\]
done
clear
E)
\[{{\left( \frac{2}{3} \right)}^{\frac{1}{2}}}\]
done
clear
View Answer play_arrow
question_answer 194) The product of the perpendicular from\[(-1,2)\] to the pair of lines\[2{{x}^{2}}-5xy+2{{y}^{2}}+3x-3y+1=0\]is:
A)
\[\frac{5}{12}\]
done
clear
B)
\[\frac{12}{5}\]
done
clear
C)
\[\frac{6}{5}\]
done
clear
D)
\[\frac{5}{6}\]
done
clear
E)
\[\frac{1}{5}\]
done
clear
View Answer play_arrow
question_answer 195) The point of the curve\[2y=3-{{x}^{2}}\]at which the tangent is parallel to the line\[x+y=0,\]is:
A)
(1, 1)
done
clear
B)
\[(1,-1)\]
done
clear
C)
\[(-1,1)\]
done
clear
D)
(0, 1)
done
clear
E)
(0, 1)
done
clear
View Answer play_arrow
question_answer 196) Distance between the pair of parallel lines \[{{x}^{2}}+2\sqrt{2}xy+2{{y}^{2}}+4x+4\sqrt{2}y-8=0\]
A)
\[\frac{4\sqrt{3}}{3}\]
done
clear
B)
\[2\sqrt{2}\]
done
clear
C)
\[4\sqrt{2}\]
done
clear
D)
\[8\]
done
clear
E)
\[4\]
done
clear
View Answer play_arrow
question_answer 197) The distance between the lines\[4x+3y=11\]and\[8x+6y=5\]is:
A)
7/2
done
clear
B)
4
done
clear
C)
7/10
done
clear
D)
3/5
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 198) The equation of the circle circumscribing the triangle formed by the lines\[x+y=6,\]\[2x+y=4\]and\[x+2y=5\]is:
A)
\[{{x}^{2}}+{{y}^{2}}+17x+19y-50=0\]
done
clear
B)
\[{{x}^{2}}+{{y}^{2}}-17x-19y-50=0\]
done
clear
C)
\[{{x}^{2}}+{{y}^{2}}+17x-19y-50=0\]
done
clear
D)
\[{{x}^{2}}+{{y}^{2}}-17x+19y+50=0\]
done
clear
E)
\[{{x}^{2}}+{{y}^{2}}-17x\,+19y+50=0\]
done
clear
View Answer play_arrow
question_answer 199) From the origin, chords are drawn to the circle\[{{x}^{2}}+{{y}^{2}}-2y=0\]. The locus of the middle points of these chords is:
A)
\[{{x}^{2}}+{{y}^{2}}-y=0\]
done
clear
B)
\[{{x}^{2}}+{{y}^{2}}-x=0\]
done
clear
C)
\[{{x}^{2}}+{{y}^{2}}-2x=0\]
done
clear
D)
\[{{x}^{2}}+{{y}^{2}}-x-y=0\]
done
clear
E)
\[{{x}^{2}}+{{y}^{2}}+y=0\]
done
clear
View Answer play_arrow
question_answer 200) The length of the tangent from (5, 1) to the circle \[{{x}^{2}}\text{+ }{{y}^{2}}+6x-4y-3=0\]is:
A)
81
done
clear
B)
49
done
clear
C)
63
done
clear
D)
21
done
clear
E)
7
done
clear
View Answer play_arrow
question_answer 201) A sphere is uniquely described, if n number of points which lie on it are given, when n is equal to:
A)
2
done
clear
B)
3
done
clear
C)
4
done
clear
D)
5
done
clear
E)
6
done
clear
View Answer play_arrow
question_answer 202) The focus of the parabola\[{{y}^{2}}=5x+4y+1\]is:
A)
(1, 2)
done
clear
B)
\[(-1,2)\]
done
clear
C)
\[(1,-2)\]
done
clear
D)
\[\left( \frac{1}{4},2 \right)\]
done
clear
E)
\[\left( -\frac{1}{4},2 \right)\]
done
clear
View Answer play_arrow
question_answer 203) The point of contact of the line\[x-y+2=0\] with the parabola\[{{y}^{2}}-8x=0\]is:
A)
(2, 4)
done
clear
B)
\[(-2,4)\]
done
clear
C)
(2, - 4)
done
clear
D)
(2, 2)
done
clear
E)
(6, 8)
done
clear
View Answer play_arrow
question_answer 204) If the length of the major axis of the ellipse\[\left( \frac{{{x}^{2}}}{{{a}^{2}}} \right)+\left( \frac{{{y}^{2}}}{{{b}^{2}}} \right)=1\]is three times the length of minor axis, its eccentricity is:
A)
\[\frac{1}{3}\]
done
clear
B)
\[\frac{1}{\sqrt{3}}\]
done
clear
C)
\[\sqrt{\frac{2}{3}}\]
done
clear
D)
\[\frac{2\sqrt{2}}{3}\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 205) S and T are the foci of the ellipse \[\left( \frac{{{x}^{2}}}{{{a}^{2}}} \right)+\left( \frac{{{y}^{2}}}{{{b}^{2}}} \right)=1\]and B is an end minor axis. If STB is an equilateral triangle, the eccentricity of the ellipse is:
A)
\[\frac{1}{4}\]
done
clear
B)
\[\frac{1}{3}\]
done
clear
C)
\[\frac{1}{2}\]
done
clear
D)
\[\sqrt{\frac{3}{2}}\]
done
clear
E)
\[\frac{1}{\sqrt{2}}\]
done
clear
View Answer play_arrow
question_answer 206) The difference of the focal distance of any point on the hyperbola is equal to its:
A)
latus rectum
done
clear
B)
eccentricity
done
clear
C)
length of the transverse axis
done
clear
D)
half the length of the transverse axis
done
clear
E)
length of the conjugate axis
done
clear
View Answer play_arrow
question_answer 207) The mean mark in Statistics of 100 students in a class was 72. The mean mark of boys was 75. While their number was 70. The mean mark of girls in the class was:
A)
69
done
clear
B)
60
done
clear
C)
66
done
clear
D)
62
done
clear
E)
65
done
clear
View Answer play_arrow
question_answer 208) The empirical relation between Mean, Median and Mode is:
A)
Mean - Median = 3 (Mode Median)
done
clear
B)
Mean - Mode = 3 (Median - Mode)
done
clear
C)
Mode - Mean = 3 (Median - Mode)
done
clear
D)
Mean - Mode = 3 (Mean - Median)
done
clear
E)
Mean - Mode = 2(Mean - Media)
done
clear
View Answer play_arrow
question_answer 209) The correlation coefficient always lies in the interval:
A)
\[(-1,1)\]
done
clear
B)
\[(-1,0)\]
done
clear
C)
(0, 1)
done
clear
D)
\[[-1,1]\]
done
clear
E)
\[\left( -\frac{1}{2},\frac{1}{2} \right)\]
done
clear
View Answer play_arrow
question_answer 210) If the correlation coefficient is zero, then the angle (in radians) between the two lines of regression is:
A)
\[\frac{\pi }{2}\]
done
clear
B)
\[0\]
done
clear
C)
\[\frac{\pi }{3}\]
done
clear
D)
\[\frac{\pi }{4}\]
done
clear
E)
\[\frac{\pi }{6}\]
done
clear
View Answer play_arrow
question_answer 211) A determinant is chosen at random from the set of all determinants of order 2 with elements 0 and 1 only. The probability that the determinant chosen is positive, is:
A)
\[\frac{1}{16}\]
done
clear
B)
\[\frac{1}{8}\]
done
clear
C)
\[\frac{3}{16}\]
done
clear
D)
\[\frac{1}{4}\]
done
clear
E)
\[\frac{1}{2}\]
done
clear
View Answer play_arrow
question_answer 212) From a box containing 10 mangoes out, of which 4 are rotten. 2 mangoes are taken out together. If one of them is found to be good, the probability that the other is also good, is:
A)
\[\frac{4}{9}\]
done
clear
B)
\[\frac{8}{15}\]
done
clear
C)
\[\frac{5}{13}\]
done
clear
D)
\[\frac{2}{3}\]
done
clear
E)
\[\frac{5}{9}\]
done
clear
View Answer play_arrow
question_answer 213) If\[A+B+C=180{}^\circ ,\]then\[\frac{\cos A+\cot B+\cot C}{\cot A\cot B\cot C}\]is equal to:
A)
1
done
clear
B)
\[cot\text{ }A\text{ }cot\text{ }B\text{ }cot\text{ }C\]
done
clear
C)
\[-1\]
done
clear
D)
0
done
clear
E)
\[cot\text{ }A+cot\text{ }B+cot\text{ }C\]
done
clear
View Answer play_arrow
question_answer 214) The angles of a triangle are in AP and the least angle is \[30{}^\circ \].The greatest angle in radians is:
A)
\[\frac{7\pi }{12}\]
done
clear
B)
\[\frac{2\pi }{3}\]
done
clear
C)
\[\frac{5\pi }{6}\]
done
clear
D)
\[\frac{\pi }{2}\]
done
clear
E)
\[\frac{\pi }{3}\]
done
clear
View Answer play_arrow
question_answer 215) If\[\tan 20{}^\circ =p,\]then\[\frac{\tan 160{}^\circ -\tan 110{}^\circ }{1+\tan 160{}^\circ \tan 110{}^\circ }\]is equal to:
A)
\[\left( \frac{1+{{p}^{2}}}{2p} \right)\]
done
clear
B)
\[\left( \frac{2p}{1+{{p}^{2}}} \right)\]
done
clear
C)
\[\left( \frac{1+p}{2p} \right)\]
done
clear
D)
\[\left( \frac{1-p}{2p} \right)\]
done
clear
E)
\[\left( \frac{1-{{p}^{2}}}{2p} \right)\]
done
clear
View Answer play_arrow
question_answer 216) The general solution of the trigonometrical equation\[sin\text{ }x+cos\text{ }x=1\]for\[n=0,\pm 1.......\]is given by:
A)
\[x=2n\pi \]
done
clear
B)
\[x=2n\pi +\pi /2\]
done
clear
C)
\[x=n\pi +{{(-1)}^{n}}\frac{\pi }{4}-\frac{\pi }{4}\]
done
clear
D)
\[x=2n\pi \]
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 217) If\[4{{\sin }^{-1}}x+{{\cos }^{-1}}x=\pi ,\]then\[x\]is equal to:
A)
\[\frac{1}{2}\]
done
clear
B)
\[2\]
done
clear
C)
\[1\]
done
clear
D)
\[\frac{1}{3}\]
done
clear
E)
\[\frac{1}{5}\]
done
clear
View Answer play_arrow
question_answer 218) In a triangle ABC,\[a=2,b=3\]and\[\sin A=\frac{2}{3}\]. Then\[cos\text{ }C\]is equal to:
A)
\[\frac{1}{2}\]
done
clear
B)
\[\frac{1}{3}\]
done
clear
C)
\[\frac{2}{\sqrt{13}}\]
done
clear
D)
\[\frac{1}{\sqrt{13}}\]
done
clear
E)
\[\frac{2}{3}\]
done
clear
View Answer play_arrow
question_answer 219) The value of\[[\overrightarrow{a}\text{ }\overrightarrow{a}+\overrightarrow{b}\text{ }\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}]\]is:
A)
\[{{[\overrightarrow{a}\text{ }\overrightarrow{b}\text{ }\overrightarrow{c}]}^{2}}\]
done
clear
B)
\[[\overrightarrow{a}\text{ }\overrightarrow{b}\text{ }\overrightarrow{c}]\]
done
clear
C)
\[2[\overrightarrow{a}\text{ }\overrightarrow{b}\text{ }\overrightarrow{c}]\]
done
clear
D)
\[3[\overrightarrow{a}\text{ }\overrightarrow{b}\text{ }\overrightarrow{c}]\]
done
clear
E)
\[[\overrightarrow{a}\text{ }\overrightarrow{b}\text{ }\overrightarrow{c}]\]
done
clear
View Answer play_arrow
question_answer 220) The vector equation \[\overrightarrow{r}=\hat{i}-2\hat{j}-\hat{k}+t(6\hat{j}-\hat{k})\] represents a straight line passing through the points:
A)
\[(0,\text{ }6,-1)\]and\[(1,-2,-1)\]
done
clear
B)
\[(0,\text{ }6,-1)\]and\[(-1,-4,-2)\]
done
clear
C)
\[(1,-2,-1)\]and \[(1,4,-2)\]
done
clear
D)
\[(1,-2,-1)\]and \[(0,-6,1)\]
done
clear
E)
\[(1,4,-2)\]and\[(2,10,-3)\]
done
clear
View Answer play_arrow
question_answer 221) If\[\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\]are non-zero, non-coplanar vectors, then\[(\overrightarrow{c}\times \overrightarrow{a})\times (\overrightarrow{a}\times \overrightarrow{b})\]is:
A)
parallel to \[\vec{a}\]
done
clear
B)
perpendicular to \[\vec{a}\]
done
clear
C)
parallel to the plane of \[\vec{b}\] and \[\vec{c}\]
done
clear
D)
perpendicular to \[\vec{c}\]
done
clear
E)
perpendicular to \[\vec{b}\]
done
clear
View Answer play_arrow
question_answer 222) If\[\overset{\to }{\mathop{PR}}\,=2\hat{i}-\hat{j}+\hat{k}\]and \[\overset{\to }{\mathop{QS}}\,=-\hat{i}+3\hat{j}+2\hat{k},\]then the area of the quadrilateral PQRS (in sq unit) with P, Q, R, S being in cyclic order, is:
A)
\[\frac{5}{2}\sqrt{3}sq\text{ }unit\]
done
clear
B)
\[10\sqrt{3}sq\text{ }unit\]
done
clear
C)
\[5\sqrt{\frac{3}{2}}sq\text{ }unit\]
done
clear
D)
\[\frac{3}{2}sq\text{ }unit\]
done
clear
E)
\[\frac{7}{2}sq\text{ }unit\]
done
clear
View Answer play_arrow
question_answer 223) The shortest distance of the point (2,10,1) from the plane\[\overrightarrow{r}.(3\hat{i}-\hat{j}+4\hat{k})=2\sqrt{26}\]is:
A)
\[2\sqrt{26}\]
done
clear
B)
\[\sqrt{26}\]
done
clear
C)
\[\frac{1}{\sqrt{26}}\]
done
clear
D)
\[4\]
done
clear
E)
\[2\]
done
clear
View Answer play_arrow
question_answer 224) If\[\overrightarrow{a}\times (\overrightarrow{b}\times \overrightarrow{c})+\overrightarrow{b}\times (\overrightarrow{c}\times \overrightarrow{a})\] \[+\overrightarrow{c}\times (\overrightarrow{a}\times \overrightarrow{b})=0,\]then:
A)
\[\vec{a}+\vec{b}+\vec{c}=0\]
done
clear
B)
\[\vec{a},\vec{b},\vec{c}\]are mutually perpendicular
done
clear
C)
\[\vec{a},\vec{b},\vec{c}\]are parallel
done
clear
D)
\[\vec{a},\vec{b},\vec{c}\]can be any three arbitrary vectors
done
clear
E)
\[\vec{a},\vec{b},\vec{c}\]are coplanar vectors
done
clear
View Answer play_arrow
question_answer 225) The magnitude of the moment of a force \[-2\hat{i}+6\hat{j}-8\hat{k}\]acting at the point\[-2\hat{i}-\hat{j}+3\hat{k}\] about the point\[\hat{i}+2\hat{j}-\hat{k}\]is:
A)
\[\sqrt{211}\]
done
clear
B)
\[40\]
done
clear
C)
\[\sqrt{54}\]
done
clear
D)
\[2\sqrt{54}\]
done
clear
E)
\[72\]
done
clear
View Answer play_arrow
question_answer 226) If\[\overrightarrow{a}=-\hat{i}+2\hat{j}-\hat{k},\overrightarrow{b}=\hat{i}+\hat{j}-3\hat{k}\]and \[\vec{c}=-4\hat{i}-\hat{k},\]then\[\overrightarrow{a}\times (\overrightarrow{b}\times \overrightarrow{c})+(\overrightarrow{a}.\overrightarrow{b}).\overrightarrow{c}\] :
A)
\[5\hat{i}+5\hat{j}-15\hat{k}\]
done
clear
B)
0
done
clear
C)
\[12\hat{j}+4\hat{k}\]
done
clear
D)
\[-3\hat{i}+6\hat{j}-3\hat{k}\]
done
clear
E)
\[7\hat{i}-7\hat{j}-19\hat{k}\]
done
clear
View Answer play_arrow
question_answer 227) The angle between straight lines\[\overrightarrow{r}=\hat{i}+2\hat{j}-\hat{k}+s(3\hat{i}-\hat{k})\]and\[\vec{r}=(1-t)(4\hat{i}-\hat{j})+t(2\hat{i}+\hat{j})-3\hat{k}\] is:
A)
0
done
clear
B)
\[{{\cos }^{-1}}\left[ \frac{18}{(15\sqrt{14})} \right]\]
done
clear
C)
\[{{\cos }^{-1}}\left[ \frac{-3}{\sqrt{20}} \right]\]
done
clear
D)
\[{{\sin }^{-1}}\left( \frac{2}{\sqrt{102}} \right)\]
done
clear
E)
\[\frac{\pi }{2}\]
done
clear
View Answer play_arrow
question_answer 228) The shortest distance between skew-lines \[\overrightarrow{r}=s\text{ }\hat{k}\]and\[\overrightarrow{r}=(1-t)\hat{i}+t\hat{j}\]is:
A)
0
done
clear
B)
\[\sqrt{2}\]
done
clear
C)
1
done
clear
D)
\[\frac{1}{\sqrt{2}}\]
done
clear
E)
2
done
clear
View Answer play_arrow
question_answer 229) The radius of the sphere passing through the points (0, 0, 0), (a, 0, 0), (0, b, O) and (0, 0, c) is:
A)
\[\frac{1}{2}{{({{a}^{2}}+{{b}^{2}}+{{c}^{2}})}^{\frac{1}{2}}}\]
done
clear
B)
\[{{({{a}^{2}}+{{b}^{2}}+{{c}^{2}})}^{\frac{1}{2}}}\]
done
clear
C)
\[2{{({{a}^{2}}+{{b}^{2}}+{{c}^{2}})}^{\frac{1}{2}}}\]
done
clear
D)
\[a+b+c\]
done
clear
E)
\[\frac{{{({{a}^{2}}+{{b}^{2}}+{{c}^{2}})}^{\frac{1}{2}}}}{\sqrt{2}}\]
done
clear
View Answer play_arrow
question_answer 230) The point, which is equidistant from the points (0, 0, 0), (2, 0, 0), (0, 2, 0) and (2, 2, 2) is:
A)
\[(1,0,1)\]
done
clear
B)
(0, 1, 1)
done
clear
C)
\[(1,1,-1)\]
done
clear
D)
(1, 1, 0)
done
clear
E)
(1, 1, 1)
done
clear
View Answer play_arrow
question_answer 231) The direction cosines of a straight line, whose projections on the co-ordinate axes, OX, OY, OZ 12,4,13 respectively, are:
A)
\[\frac{12}{29},\frac{4}{29},\frac{13}{29}\]
done
clear
B)
\[\frac{12}{139},\frac{4}{\sqrt{329}},\frac{13}{\sqrt{329}}\]
done
clear
C)
\[\frac{1}{12},\frac{1}{4},\frac{1}{13}\]
done
clear
D)
\[\frac{12}{329},\frac{4}{329},\frac{13}{329}\]
done
clear
E)
\[\frac{12}{13},\frac{4}{13},1\]
done
clear
View Answer play_arrow
question_answer 232) The work done by the force\[4\hat{i}-3\hat{j}+2\hat{k}\]in moving a particle along a straight line from the point \[(3,2,-1)\] to\[(2,-1,4)\]is:
A)
0 unit
done
clear
B)
4 unit
done
clear
C)
15 unit
done
clear
D)
19 unit
done
clear
E)
23 unit
done
clear
View Answer play_arrow
question_answer 233) The volume (in cubic unit) of the parallelepiped whose edges are represented by the vectors\[\hat{i}+\hat{j},\text{ }\hat{j}+\hat{k}\]and\[\hat{k}+\hat{i}\]is:
A)
2
done
clear
B)
0
done
clear
C)
\[\sqrt{2}\]
done
clear
D)
\[2\sqrt{2}\]
done
clear
E)
4
done
clear
View Answer play_arrow
question_answer 234) If the points (1, 0, 3),\[(-1,\text{ }3,\text{ }4),\](1, 2,1) and (k, 2, 5) are coplanar, then k is equal to:
A)
1
done
clear
B)
2
done
clear
C)
0
done
clear
D)
\[-1\]
done
clear
E)
\[-2\]
done
clear
View Answer play_arrow
question_answer 235) For any vector\[\vec{r}\],the value of\[\hat{i}\times (\overrightarrow{r}\times \hat{i})+\hat{j}\times (\overrightarrow{r}\times \hat{j})+\hat{k}\times (\overrightarrow{r}\times \hat{k})\]is:
A)
\[\overrightarrow{0}\]
done
clear
B)
\[2\overrightarrow{r}\]
done
clear
C)
\[-2\overrightarrow{r}\]
done
clear
D)
\[3\overrightarrow{r}\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 236) If\[\overrightarrow{a}\]is a constant vector, the equation\[(\overrightarrow{r}-\overrightarrow{a}).\overrightarrow{r}=0\]represents:
A)
plane
done
clear
B)
sphere
done
clear
C)
circle
done
clear
D)
straight line
done
clear
E)
parabola
done
clear
View Answer play_arrow
question_answer 237) \[\underset{x\to 1}{\mathop{\lim }}\,\frac{{{x}^{2}}-2x+1}{|{{x}^{2}}-1|}\]is equal to:
A)
0
done
clear
B)
1
done
clear
C)
\[-1\]
done
clear
D)
2
done
clear
E)
does not exist
done
clear
View Answer play_arrow
question_answer 238) \[\underset{x\to 0}{\mathop{\lim }}\,\left( \frac{{{a}^{x}}-{{b}^{x}}}{x} \right)\]is equal to:
A)
0
done
clear
B)
1
done
clear
C)
\[log\text{ }a-log\text{ }b\]
done
clear
D)
\[log\text{ }a/log\text{ }b\]
done
clear
E)
does not exist
done
clear
View Answer play_arrow
question_answer 239) \[\underset{x\to 0}{\mathop{\lim }}\,\left( \frac{(2+x)\sin (2+x)-2\sin 2}{x} \right)\]is equal to:
A)
\[sin\text{ }2\]
done
clear
B)
\[cos\text{ }2\]
done
clear
C)
1
done
clear
D)
\[2\text{ }cos\text{ }2+sin\text{ }2\]
done
clear
E)
\[2\text{ }sin\text{ }2+cos\text{ }2\]
done
clear
View Answer play_arrow
question_answer 240) If\[f(x)=\frac{3x+{{\tan }^{2}}x}{x}\]is continuous at\[x=0,\]then\[f(x)\]is equal to:
A)
1
done
clear
B)
2
done
clear
C)
4
done
clear
D)
0
done
clear
E)
3
done
clear
View Answer play_arrow
question_answer 241) If\[|f(x)|\]is continuous at\[x=a,\]then\[f(x)\]is:
A)
continuous at \[x=a\]
done
clear
B)
continuous at\[x=-a\]
done
clear
C)
continuous at\[x=\sqrt{a}\]
done
clear
D)
not continuous at\[x=-a\]
done
clear
E)
not be continuous at\[x=a\]
done
clear
View Answer play_arrow
question_answer 242) If\[x\]is measured in degrees, then,\[\frac{d}{dx}(\cos x)\]is equal to:
A)
\[-\sin x\]
done
clear
B)
\[\frac{-180}{\pi }\sin x\]
done
clear
C)
\[\frac{\pi }{180}\sin x\]
done
clear
D)
\[\sin x\]
done
clear
E)
\[-\frac{\pi }{180}\sin x\]
done
clear
View Answer play_arrow
question_answer 243) \[\left( \frac{d}{dx} \right)[\log (\sec x-\tan x)]\]is equal to:
A)
\[-sec\text{ }x\]
done
clear
B)
\[sec\text{ }x+tan\text{ }x\]
done
clear
C)
\[sec\text{ }x\]
done
clear
D)
\[sec\text{ }x-tan\text{ }x\]
done
clear
E)
\[tan\text{ }x-sec\text{ }x\]
done
clear
View Answer play_arrow
question_answer 244) If\[x={{\cos }^{3}}\theta \]and\[y={{\sin }^{3}}\theta ,\]then\[1+{{\left( \frac{dy}{dx} \right)}^{2}}\]is equal to:
A)
\[ta{{n}^{2}}\theta \]
done
clear
B)
\[co{{t}^{2}}\theta \]
done
clear
C)
\[se{{c}^{2}}\theta \]
done
clear
D)
\[cose{{c}^{2}}\theta \]
done
clear
E)
\[se{{c}^{3}}\theta \]
done
clear
View Answer play_arrow
question_answer 245) If\[xy=x+y,\]then\[\left( \frac{dy}{dx} \right)\]is equal to:
A)
\[\frac{xy}{(1-x)}\]
done
clear
B)
\[\frac{(1+y)}{(1-x)}\]
done
clear
C)
\[\frac{y}{(1-xy)}\]
done
clear
D)
\[\frac{-1}{{{(x-1)}^{2}}}\]
done
clear
E)
\[\frac{1}{({{x}^{2}}-1)}\]
done
clear
View Answer play_arrow
question_answer 246) If\[x=a{{t}^{2}},y=2at,\]at, then\[\frac{{{d}^{2}}y}{d{{x}^{2}}}\]is equal to:
A)
\[-\frac{1}{{{t}^{2}}}\]
done
clear
B)
\[-\frac{1}{2a{{t}^{3}}}\]
done
clear
C)
\[\frac{1}{{{t}^{2}}}\]
done
clear
D)
\[-\frac{a}{2{{t}^{3}}}\]
done
clear
E)
zero
done
clear
View Answer play_arrow
question_answer 247) The value of\[x,\]for which\[|x|,\]is continuous but not differentiable, is:
A)
\[-1\]
done
clear
B)
1
done
clear
C)
0
done
clear
D)
10
done
clear
E)
does not exist, i.e., it is differentiable every where.
done
clear
View Answer play_arrow
question_answer 248) \[\frac{{{d}^{20}}}{d{{x}^{20}}}(2\cos x\cos 3x)\]is equal to:
A)
\[{{2}^{20}}(\cos 2x+{{2}^{20}}\cos 4x)\]
done
clear
B)
\[{{2}^{20}}(\cos 2x-{{2}^{20}}\sin 2x)\]
done
clear
C)
\[-6\sin x\sin 3x\]
done
clear
D)
\[6\sin x\sin 3x\]
done
clear
E)
\[6({{2}^{20}}\cos 2x-{{2}^{40}}\cos 4x)\]
done
clear
View Answer play_arrow
question_answer 249) If the rate of change in the circumference of a circle is 0.3 cm/s, then the rate of change in the area of the circle when the radius is 5 cm, is:
A)
1.5 sq cm/s
done
clear
B)
0.5 sq cm/s
done
clear
C)
5 sq cm/s
done
clear
D)
3 sq cm/s
done
clear
E)
0.04 sq cm/s
done
clear
View Answer play_arrow
question_answer 250) A particle moves along a straight line according to the law\[s={{e}^{t}}(\sin t-\cos t)\]. The acceleration. at any time t is:
A)
\[{{e}^{t}}(\cos t+\sin t)\]
done
clear
B)
\[{{e}^{t}}(\cos t-\sin t)\]
done
clear
C)
\[2{{e}^{t}}(\cos t-\sin t)\]
done
clear
D)
\[2{{e}^{t}}(\cos t+\sin t)\]
done
clear
E)
\[{{e}^{2t}}(\sin t-\cos t)\]
done
clear
View Answer play_arrow
question_answer 251) If\[y={{x}^{3}}-a{{x}^{2}}+48x+7\]is an increasing function for all real values of\[x,\]then a lies in:
A)
\[(-14,14)\]
done
clear
B)
\[(-12,12)\]
done
clear
C)
\[(-16,16)\]
done
clear
D)
\[(-21,21)\]
done
clear
E)
\[(0,\text{ }a)\]
done
clear
View Answer play_arrow
question_answer 252) The value of a for which the function\[f(x)=\]\[a\sin x+\left( \frac{1}{3} \right)\sin 3x\]has an extremum at\[x=3,\]is:
A)
1
done
clear
B)
\[-1\]
done
clear
C)
2
done
clear
D)
0
done
clear
E)
\[-2\]
done
clear
View Answer play_arrow
question_answer 253) If\[lo{{g}_{e}}4=1.3868,\]then the approximate value of\[lo{{g}_{e}}4.01\]is:
A)
0.13893
done
clear
B)
1.3843
done
clear
C)
1.3893
done
clear
D)
0.13843
done
clear
E)
1.3869
done
clear
View Answer play_arrow
question_answer 254) Rolles theorem is not applicable for the function\[f(x)=|x|\]in the interval\[[-1,1]\]because:
A)
\[f(1)\]does not exist
done
clear
B)
\[f(-1)\]does not exist
done
clear
C)
\[f(x)\]is discontinuous at\[x=0\]
done
clear
D)
\[f(0)\]does not exist
done
clear
E)
\[f(x)\]is discontinuous at\[x=\pm 1\]
done
clear
View Answer play_arrow
question_answer 255) \[\int{\frac{2dx}{{{({{e}^{x}}+{{e}^{-x}})}^{2}}}}\]is equal to:
A)
\[\frac{-{{e}^{-x}}}{({{e}^{x}}+{{e}^{-x}})}+c\]
done
clear
B)
\[\frac{-1}{({{e}^{x}}+{{e}^{-x}})}+c\]
done
clear
C)
\[\frac{1}{{{({{e}^{x}}+1)}^{2}}}+c\]
done
clear
D)
\[\frac{1}{{{({{e}^{x}}+{{e}^{-x}})}^{2}}}+c\]
done
clear
E)
\[\frac{1}{({{e}^{x}}-{{e}^{-x}})}+c\]
done
clear
View Answer play_arrow
question_answer 256) \[\int{\frac{{{x}^{3}}}{x+1}}dx\]is equal to:
A)
\[\frac{{{x}^{3}}}{3}-\frac{{{x}^{2}}}{2}+c\]
done
clear
B)
\[\frac{{{x}^{3}}}{3}-\frac{{{x}^{2}}}{2}+x-\log (x+1)+c\]
done
clear
C)
\[\frac{{{x}^{3}}}{3}-\frac{{{x}^{2}}}{2}+x+\log (x+1)+c\]
done
clear
D)
\[\frac{{{x}^{4}}}{2{{(x+1)}^{2}}}+c\]
done
clear
E)
\[\frac{{{x}^{3}}}{3}+\frac{{{x}^{4}}}{4}+c\]
done
clear
View Answer play_arrow
question_answer 257) \[\int{\frac{{{e}^{x}}(1+x)}{{{\cos }^{2}}(x{{e}^{x}})}dx}\]is equal to:
A)
\[2\log \cos (x{{e}^{x}})+c\]
done
clear
B)
\[\sec (x{{e}^{x}})+c\]
done
clear
C)
\[\tan (x{{e}^{x}})+c\]
done
clear
D)
\[\tan (x+{{e}^{x}})+c\]
done
clear
E)
\[{{e}^{x}}\tan (x{{e}^{x}})+c\]
done
clear
View Answer play_arrow
question_answer 258) \[\int{{{a}^{x}}{{e}^{x}}}dx\]is equal to:
A)
\[{{a}^{x}}{{e}^{x}}+c\]
done
clear
B)
\[\left[ \frac{{{a}^{x}}{{e}^{x}}}{\log a} \right]+c\]
done
clear
C)
\[\left[ \frac{{{(ae)}^{x}}}{(x+1)} \right]+c\]
done
clear
D)
\[\left[ \frac{{{a}^{x}}{{e}^{x}}}{1+\log a} \right]+c\]
done
clear
E)
\[\frac{{{e}^{x}}{{a}^{x}}}{(a+1)}+c\]
done
clear
View Answer play_arrow
question_answer 259) \[\int{\frac{4x}{({{x}^{2}}+1)({{x}^{2}}+3)}}dx\]is equal to:
A)
\[\log \left[ \frac{{{x}^{2}}+1}{{{x}^{2}}+3} \right]+c\]
done
clear
B)
\[\log \left[ \frac{{{x}^{2}}+3}{{{x}^{2}}+1} \right]+c\]
done
clear
C)
\[{{\tan }^{-1}}x+\left( \frac{1}{\sqrt{3}} \right){{\tan }^{-1}}\left( \frac{x}{\sqrt{3}} \right)+c\]
done
clear
D)
\[\left( \frac{4}{\sqrt{3}} \right){{\tan }^{-1}}x{{\tan }^{-1}}\left( \frac{x}{\sqrt{3}} \right)+c\]
done
clear
E)
\[2\log ({{x}^{2}}+1)({{x}^{2}}+3)+c\]
done
clear
View Answer play_arrow
question_answer 260) \[\int{\frac{{{\sin }^{2}}x}{{{\cos }^{4}}x}}dx\]is equal to:
A)
\[\frac{1}{3}{{\tan }^{2}}x+c\]
done
clear
B)
\[\frac{1}{2}{{\tan }^{2}}x+c\]
done
clear
C)
\[\frac{1}{3}{{\tan }^{3}}x+c\]
done
clear
D)
\[3\sin 2x-4\cos 4x+c\]
done
clear
E)
\[{{\cos }^{3}}x+c\]
done
clear
View Answer play_arrow
question_answer 261) \[\int_{-1/2}^{1/2}{\frac{dx}{{{(1-{{x}^{2}})}^{1/2}}}}\]is equal to:
A)
\[\frac{\pi }{6}\]
done
clear
B)
\[\frac{\pi }{4}\]
done
clear
C)
\[\frac{\pi }{2}\]
done
clear
D)
0
done
clear
E)
\[\frac{\pi }{3}\]
done
clear
View Answer play_arrow
question_answer 262) \[\int_{0}^{\frac{\pi }{2}}{\frac{{{\sin }^{n}}\theta }{{{\sin }^{n}}\theta +{{\cos }^{n}}\theta }}d\theta \]is equal to:
A)
\[1\]
done
clear
B)
\[0\]
done
clear
C)
\[\frac{\pi }{2}\]
done
clear
D)
\[\frac{\pi }{4}\]
done
clear
E)
\[\pi \]
done
clear
View Answer play_arrow
question_answer 263) \[\int_{0}^{\pi }{{{\cos }^{101}}xdx}\]is equal to:
A)
\[\frac{\pi }{4}\]
done
clear
B)
\[\frac{1}{102}\]
done
clear
C)
\[{{\left( \frac{\pi }{3} \right)}^{101}}\]
done
clear
D)
\[0\]
done
clear
E)
\[-1\]
done
clear
View Answer play_arrow
question_answer 264) The area in sq unit enclosed by the curve\[y=4{{x}^{3}}\]the\[x-\]axis and the lines\[x=6\]and\[x=9\]is:
A)
2 sq unit
done
clear
B)
1 sq unit
done
clear
C)
4 sq unit
done
clear
D)
3 sq unit
done
clear
E)
6 sq unit
done
clear
View Answer play_arrow
question_answer 265) The area (in square unit) enclosed by the curves\[y=4{{x}^{3}}\]and\[y=16x,\]is:
A)
16 sq unit
done
clear
B)
32 sq unit
done
clear
C)
\[\frac{1}{4}\]sq unit
done
clear
D)
\[\frac{1}{2}\]sq unit
done
clear
E)
\[\frac{1}{8}\]sq unit
done
clear
View Answer play_arrow
question_answer 266) \[\underset{n\to \infty }{\mathop{\lim }}\,\left[ \frac{1}{n+1}+\frac{1}{n+2}+....+\frac{1}{6n} \right]\]:
A)
\[log\text{ }2\]
done
clear
B)
\[\log (1+\sqrt{5})\]
done
clear
C)
\[log\text{ }6\]
done
clear
D)
0
done
clear
E)
\[log\text{ }5\]
done
clear
View Answer play_arrow
question_answer 267) The degree of the differential equations \[{{\left[ 5+{{\left( \frac{dy}{dx} \right)}^{2}} \right]}^{\frac{5}{3}}}={{x}^{5}}\left[ \frac{{{d}^{2}}y}{d{{x}^{2}}} \right]\]is.
A)
4
done
clear
B)
2
done
clear
C)
5
done
clear
D)
10
done
clear
E)
3
done
clear
View Answer play_arrow
question_answer 268) By eliminating the arbitrary constants A and B from\[y=A{{x}^{2}}+Bx,\]we get the differential equation:
A)
\[\frac{{{d}^{3}}y}{d{{x}^{3}}}=0\]
done
clear
B)
\[{{x}^{2}}\frac{{{d}^{2}}y}{d{{x}^{2}}}-2x\frac{dy}{dx}+2y=0\]
done
clear
C)
\[\frac{{{d}^{2}}y}{d{{x}^{2}}}=0\]
done
clear
D)
\[{{x}^{2}}\frac{{{d}^{2}}y}{d{{x}^{2}}}+y=0\]
done
clear
E)
\[2\frac{{{d}^{2}}y}{d{{x}^{2}}}+\frac{dy}{dx}=0\]
done
clear
View Answer play_arrow
question_answer 269) The general solution of \[x{{(1+{{y}^{2}})}^{\frac{1}{2}}}dx+y{{(1+{{x}^{2}})}^{1/2}}dy=0\]is:
A)
\[{{\sin }^{-1}}x+{{\sin }^{-1}}y=c\]
done
clear
B)
\[{{x}^{2}}+{{y}^{2}}={{(1+{{x}^{2}})}^{1/2}}+{{(1+{{y}^{2}})}^{1/2}}+c\]
done
clear
C)
\[{{(1+{{x}^{2}})}^{1/2}}+{{(1+{{y}^{2}})}^{1/2}}=c\]
done
clear
D)
\[{{\tan }^{-1}}x-{{\tan }^{-1}}y=c\]
done
clear
E)
\[{{\cos }^{-1}}x+{{\cos }^{-1}}y=c\]
done
clear
View Answer play_arrow
question_answer 270) The general solution of\[(x+1)\frac{dy}{dx}+1=2{{e}^{-y}}\]is.
A)
\[{{e}^{y}}=2x+c\]
done
clear
B)
\[{{e}^{-y}}=2x+c\]
done
clear
C)
\[{{e}^{y}}(x+1)=2x+c\]
done
clear
D)
\[{{e}^{y}}(x+1)+c\]
done
clear
E)
\[{{e}^{y}}(x+1)=x+c\]
done
clear
View Answer play_arrow
question_answer 271) The general solution of \[(2x-y+1)dx+(2y-x+1)dx=0\]is:
A)
\[{{x}^{2}}-xy+{{y}^{2}}+x+y=c\]
done
clear
B)
\[{{x}^{2}}-xy-{{y}^{2}}+x+y=c\]
done
clear
C)
\[{{x}^{2}}-xy+{{y}^{2}}+x-y=c\]
done
clear
D)
\[{{x}^{2}}+xy+{{y}^{2}}+x+y=c\]
done
clear
E)
\[{{x}^{2}}-xy-{{y}^{2}}-x-y=c\]
done
clear
View Answer play_arrow
question_answer 272) The general solution of\[\frac{dy}{dx}+y\cot x=\cos ecx\]is:
A)
\[x+y\text{ }sin\text{ }x=c\]
done
clear
B)
\[x+y\text{ }cos\text{ }x=c\]
done
clear
C)
\[y=x(sin\text{ }x+cos\text{ }x)+c\]
done
clear
D)
\[y\text{ }sin\text{ }x=x+c\]
done
clear
E)
\[y\text{ }co{{s}^{2}}\text{ }x+\text{ }x=c\]
done
clear
View Answer play_arrow
question_answer 273) \[\underset{x\to 3}{\mathop{\lim }}\,\frac{{{x}^{2}}-9}{|x-3|}\]:
A)
0
done
clear
B)
3
done
clear
C)
\[\infty \]
done
clear
D)
6
done
clear
E)
does not exist
done
clear
View Answer play_arrow
question_answer 274) In the set\[{{Q}^{+}}\]of all positive rational numbers, the operation * is defined by the formula\[a*.b=\frac{ab}{6}.\]Then the inverse of 9 with respect to * is:
A)
\[4\]
done
clear
B)
3
done
clear
C)
\[\frac{1}{9}\]
done
clear
D)
\[\frac{1}{3}\]
done
clear
E)
\[\frac{2}{3}\]
done
clear
View Answer play_arrow
question_answer 275) If\[f(x)=\frac{\log (1+ax)-\log (1-bx)}{x}\]for\[x\ne 0\]and \[f(0)=k\]and\[f(x)\] is continuous at\[x=0\]then k is equal to:
A)
\[a+b\]
done
clear
B)
\[a-b\]
done
clear
C)
\[a\]
done
clear
D)
\[b\]
done
clear
E)
\[b-a\]
done
clear
View Answer play_arrow
question_answer 276) If\[f(x)=\log \left( \frac{1-x}{1+x} \right),\]then\[f(a)+f(b)\]is equal to:
A)
\[f(a+b)\]
done
clear
B)
\[f(ab)\]
done
clear
C)
\[f\left( \frac{a+b}{1+ab} \right)\]
done
clear
D)
\[0\]
done
clear
E)
\[f\left( \frac{a-b}{1+ab} \right)\]
done
clear
View Answer play_arrow
question_answer 277) If\[f(x)=x-{{x}^{2}}+{{x}^{3}}-{{x}^{4}}+....\]to\[\infty \]for\[|x|<1,\]then\[{{f}^{-1}}(x)\]is equal to:
A)
\[x\]
done
clear
B)
\[\left( \frac{x}{1-x} \right)\]
done
clear
C)
\[\frac{1-x}{x}\]
done
clear
D)
\[\frac{1}{x}\]
done
clear
E)
\[\left( \frac{x}{1+x} \right)\]
done
clear
View Answer play_arrow
question_answer 278) If\[f:R\to R\]is defined by\[f(x)=3x+|x|,\]then \[f(2x)-f(-x)-6x\]is equal to:
A)
\[3f(x)\]
done
clear
B)
\[2f(x)\]
done
clear
C)
\[-f(x)\]
done
clear
D)
\[f(-x)\]
done
clear
E)
\[f(x)\]
done
clear
View Answer play_arrow
question_answer 279) If\[4-5i\]is a root of the quadratic equation \[x+ax+b=0,\]then (a, b) is equal to:
A)
(8, 41)
done
clear
B)
\[(-8,41)\]
done
clear
C)
(41, 8)
done
clear
D)
\[(-41,8)\]
done
clear
E)
\[(-8,-41)\]
done
clear
View Answer play_arrow
question_answer 280) If\[\alpha \]and\[\beta \]are the roots of the quadratic equation\[4{{x}^{2}}+3x+7=0,\]then the value of\[\frac{1}{\alpha }+\frac{1}{\beta }\]is:
A)
\[-\frac{3}{4}\]
done
clear
B)
\[-\frac{3}{7}\]
done
clear
C)
\[\frac{3}{7}\]
done
clear
D)
\[\frac{4}{7}\]
done
clear
E)
\[\frac{3}{4}\]
done
clear
View Answer play_arrow
question_answer 281) If\[\alpha ,\beta \]are the roots of\[a{{x}^{2}}+bx+c=0\]and \[\alpha +k,\text{ }\beta +k\]are the roots of\[p{{x}^{2}}+qx+r=0,\] then\[\frac{{{b}^{2}}-4ac}{{{q}^{2}}-4pr}\]is equal to:
A)
\[\frac{a}{p}\]
done
clear
B)
\[1\]
done
clear
C)
\[{{\left( \frac{a}{p} \right)}^{2}}\]
done
clear
D)
\[0\]
done
clear
E)
\[{{\left( \frac{p}{a} \right)}^{2}}\]
done
clear
View Answer play_arrow
question_answer 282) If\[3{{p}^{2}}=5p+2\]and\[3{{q}^{2}}=5q+2\]where\[n\ne q,\] then the equation whose roots are\[3p-2q\]and\[3q-2p\]is:
A)
\[5{{x}^{2}}-3x-100=0\]
done
clear
B)
\[5{{x}^{2}}+3x+100=0\]
done
clear
C)
\[3{{x}^{2}}-5x+100=0\]
done
clear
D)
\[3{{x}^{2}}+5x-100=0\]
done
clear
E)
\[3{{x}^{2}}-5x-100=0\]
done
clear
View Answer play_arrow
question_answer 283) If p, q are the roots of\[a{{x}^{2}}-25x+c=0,\]then \[{{p}^{3}}{{q}^{3}}+{{p}^{2}}{{q}^{3}}+{{p}^{3}}{{q}^{2}}\]is equal to:
A)
\[{{c}^{2}}\left( \frac{c+25}{{{a}^{3}}} \right)\]
done
clear
B)
\[{{c}^{3}}{{\left( \frac{c-25}{{{a}^{2}}} \right)}^{2}}\]
done
clear
C)
\[\frac{b{{c}^{3}}}{{{a}^{3}}}\]
done
clear
D)
\[\frac{b{{c}^{2}}}{a}\]
done
clear
E)
\[{{c}^{2}}\left( \frac{c-25}{{{a}^{3}}} \right)\]
done
clear
View Answer play_arrow
question_answer 284) If the ratio of the roots of\[{{x}^{2}}+bx+c=0\]and \[{{x}^{2}}+qx+r=0\]is the same, then:
A)
\[{{r}^{2}}b=q{{c}^{2}}\]
done
clear
B)
\[r{{b}^{2}}=c{{q}^{2}}\]
done
clear
C)
\[{{r}^{2}}c=q{{b}^{2}}\]
done
clear
D)
\[r{{c}^{2}}=b{{q}^{2}}\]
done
clear
E)
\[{{r}^{2}}q={{c}^{2}}b\]
done
clear
View Answer play_arrow
question_answer 285) Area of the triangle in the argand diagram formed by the complex numbers\[z,iz,z+iz,\] where\[z=x+iy,\]is:
A)
\[|z|\]
done
clear
B)
\[|z{{|}^{2}}\]
done
clear
C)
\[2|z{{|}^{2}}\]
done
clear
D)
\[\frac{1}{2}|z{{|}^{2}}\]
done
clear
E)
\[\frac{1}{2}|z|\]
done
clear
View Answer play_arrow
question_answer 286) If\[\omega \]is an imaginary cube root of 1, then\[{{(1+\omega +{{\omega }^{2}})}^{6}}+{{(1-\omega +{{\omega }^{2}})}^{5}}\]is equal to:
A)
16
done
clear
B)
8
done
clear
C)
9
done
clear
D)
27
done
clear
E)
32
done
clear
View Answer play_arrow
question_answer 287) If\[|z-3+i|=4,\]then locus of z is:
A)
\[{{x}^{2}}+{{y}^{2}}-6x+2y-6=0\]
done
clear
B)
\[{{x}^{2}}+{{y}^{2}}-6=0\]
done
clear
C)
\[{{x}^{2}}+{{y}^{2}}-3x+y-6=0\]
done
clear
D)
\[{{x}^{2}}+{{y}^{2}}=0\]
done
clear
E)
\[{{x}^{2}}-{{y}^{2}}-6x-2y-8=0\]
done
clear
View Answer play_arrow
question_answer 288) If\[x\]satisfies\[{{x}^{2}}-2x\text{ }cos\theta +1=0,\]then the value of\[\left( {{x}^{n}}+\frac{1}{{{x}^{n}}} \right)\]is:
A)
\[{{2}^{n}}\cos n\theta \]
done
clear
B)
\[{{2}^{n}}{{\cos }^{n}}\theta \]
done
clear
C)
\[2{{\cos }^{n}}\theta \]
done
clear
D)
\[2\cos n\theta \]
done
clear
E)
\[2\sin n\theta \]
done
clear
View Answer play_arrow
question_answer 289) The value of \[{{\left[ -\frac{1}{2}+i\frac{\sqrt{3}}{2} \right]}^{3n}}+{{\left[ -\frac{1}{2}-i\frac{\sqrt{3}}{2} \right]}^{3n}}\]is:
A)
0
done
clear
B)
1
done
clear
C)
2
done
clear
D)
3
done
clear
E)
\[-2\]
done
clear
View Answer play_arrow
question_answer 290) If\[\theta =\frac{\pi }{6},\]then the 10th term of the series\[1+(\cos \theta +i\sin \theta )+{{(\cos \theta +i\sin \theta )}^{2}}+...\]is:
A)
\[-1\]
done
clear
B)
\[-i\]
done
clear
C)
\[\frac{1+i\sqrt{3}}{2}\]
done
clear
D)
\[\frac{1-i\sqrt{3}}{2}\]
done
clear
E)
\[-i\]
done
clear
View Answer play_arrow
question_answer 291) The sum of n terms of the series\[\frac{1}{2}+\frac{3}{4}+\frac{7}{8}+\frac{15}{16}+....\]is:
A)
\[n-1+{{2}^{-n}}\]
done
clear
B)
\[1\]
done
clear
C)
\[n-1\]
done
clear
D)
\[1+{{2}^{-n}}\]
done
clear
E)
\[n-1-{{2}^{-n}}\]
done
clear
View Answer play_arrow
question_answer 292) \[0.2+0.22+0.222+...\]to n terms is equal to:
A)
\[\left( \frac{2}{9} \right)-\left( \frac{2}{81} \right)(1-{{10}^{-n}})\]
done
clear
B)
\[n-\left( \frac{1}{9} \right)(1-{{10}^{-n}})\]
done
clear
C)
\[\left( \frac{2}{9} \right)\left[ n-\left( \frac{1}{9} \right)(1-{{10}^{-n}}) \right]\]
done
clear
D)
\[\left( \frac{2}{9} \right)\]
done
clear
E)
\[\left( \frac{2}{9} \right)\left[ n-\left( \frac{1}{9} \right)(1-{{10}^{n}}) \right]\]
done
clear
View Answer play_arrow
question_answer 293) If\[\frac{{{a}^{n+1}}+{{b}^{n+1}}}{{{a}^{n}}+{{b}^{n}}}\]the arithmetic mean between a and b, then n is equal to:
A)
2
done
clear
B)
\[-2\]
done
clear
C)
0
done
clear
D)
1
done
clear
E)
\[-1\]
done
clear
View Answer play_arrow
question_answer 294) If\[{{(i)}^{2}}=-1,({{i}^{2}})+{{(i)}^{4}}+{{(i)}^{6}}+...\]to\[(2n+1)\]terms is equal to:
A)
\[-1\]
done
clear
B)
1
done
clear
C)
0
done
clear
D)
2
done
clear
E)
\[-2\]
done
clear
View Answer play_arrow
question_answer 295) If\[{{S}_{n}}\]denotes the sum of n terms of an AP, then\[{{S}_{n+3}}-3{{S}_{n+2}}+3{{S}_{n+1}}-{{S}_{n}}\]is equal to:
A)
3
done
clear
B)
1
done
clear
C)
\[\frac{1}{2}\]
done
clear
D)
2
done
clear
E)
0
done
clear
View Answer play_arrow
question_answer 296) The HM of 2 numbers is 4. Their AM is A and GM is G. If G satisfies\[2A+{{G}^{2}}=27,\]the numbers are:
A)
6, 9
done
clear
B)
9, 12
done
clear
C)
3, 6
done
clear
D)
4, 8
done
clear
E)
1, 13
done
clear
View Answer play_arrow
question_answer 297) The number of ways in which a team of 11 players can be selected from 22 players including 2 of them and excluding 4 of them is:
A)
\[^{16}{{C}_{11}}\]
done
clear
B)
\[^{16}{{C}_{5}}\]
done
clear
C)
\[^{16}{{C}_{9}}\]
done
clear
D)
\[^{20}{{C}_{8}}\]
done
clear
E)
\[^{22}{{C}_{11-2}}\]
done
clear
View Answer play_arrow
question_answer 298) There are\[(n+1)\]white and\[(n+1)\]black balls, each set of numbered 1 to\[n+1\]. The number of ways the balls can be arranged in a row so that adjacent balls are of different colours, is:
A)
\[(2n+1)!\]
done
clear
B)
\[2(2n)!\]
done
clear
C)
\[2[(n+1)!]\]
done
clear
D)
\[2{{[(n+1)!]}^{2}}\]
done
clear
E)
\[{{[(n+1)!]}^{2}}\]
done
clear
View Answer play_arrow
question_answer 299) If T denotes the r th term in the expansion of \[{{\left[ x+\frac{1}{x} \right]}^{23}},\]then:
A)
\[{{T}_{12}}={{T}_{13}}\]
done
clear
B)
\[{{x}^{2}}{{T}_{13}}={{T}_{12}}\]
done
clear
C)
\[{{T}_{12}}=x{{T}_{12}}\]
done
clear
D)
\[{{T}_{12}}+{{T}_{13}}=25\]
done
clear
E)
\[{{x}^{2}}{{T}_{12}}={{T}_{13}}\]
done
clear
View Answer play_arrow
question_answer 300) If the coefficients of second, third and fourth terms in the expansion of\[{{(1+x)}^{n}}\]are in AP, then n is equal to:
A)
3
done
clear
B)
4
done
clear
C)
5
done
clear
D)
6
done
clear
E)
7
done
clear
View Answer play_arrow
question_answer 301) The number of non-zero terms in the expansion of\[{{[1+3{{(2x)}^{1/2}}]}^{9}}+{{[1-3{{(2x)}^{1/2}}]}^{9}}\]is:
A)
9
done
clear
B)
0
done
clear
C)
10
done
clear
D)
6
done
clear
E)
5
done
clear
View Answer play_arrow
question_answer 302) The term independent of\[x\]in the expansion of \[{{(1+x)}^{n}}{{\left[ 1+\left( \frac{1}{x} \right) \right]}^{n}}\]is:
A)
\[C_{0}^{2}+2C_{1}^{2}+3C_{2}^{2}+...+(n+1)C_{n}^{2}\]
done
clear
B)
\[{{C}_{1}}+{{C}_{2}}+{{C}_{3}}+....+{{C}_{n}}\]
done
clear
C)
\[C_{0}^{2}+C_{1}^{2}+C_{2}^{2}+....+C_{n}^{2}\]
done
clear
D)
\[{{C}_{1}}+2{{C}_{2}}+3{{C}_{3}}+....+n{{C}_{n}}\]
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 303) If\[\Delta =\left| \begin{matrix} 1 & a & {{a}^{2}} \\ 1 & b & {{b}^{2}} \\ 1 & c & {{c}^{2}} \\ \end{matrix} \right|=k(a-b)(b-c)(c-a),\] then k is equal to:
A)
\[-2\]
done
clear
B)
1
done
clear
C)
2
done
clear
D)
\[abc\]
done
clear
E)
\[-1\]
done
clear
View Answer play_arrow
question_answer 304) \[\left| \begin{matrix} a+b & a & b \\ a & a+c & c \\ b & c & b+c \\ \end{matrix} \right|\]is equal to:
A)
\[4abc\]
done
clear
B)
\[abc\]
done
clear
C)
\[{{a}^{2}}{{b}^{2}}{{c}^{2}}\]
done
clear
D)
\[4{{a}^{2}}bc\]
done
clear
E)
\[4{{a}^{2}}{{b}^{2}}{{c}^{2}}\]
done
clear
View Answer play_arrow
question_answer 305) lf \[{{\Delta }_{1}}=\left| \begin{matrix} x & a & b \\ b & x & a \\ a & b & x \\ \end{matrix} \right|\] and \[{{\Delta }_{2}}=\left| \begin{matrix} x & b \\ a & x \\ \end{matrix} \right|\]are the given determinants, then:
A)
\[{{\Delta }_{1}}=3{{({{\Delta }_{2}})}^{2}}\]
done
clear
B)
\[\left( \frac{d}{dx} \right)({{\Delta }_{1}})=3{{\Delta }_{2}}\]
done
clear
C)
\[\left( \frac{d}{dx} \right)({{\Delta }_{1}})=3{{({{\Delta }_{2}})}^{2}}\]
done
clear
D)
\[{{\Delta }_{1}}\,=3{{({{\Delta }_{2}})}^{3/2}}\]
done
clear
E)
\[\left( \frac{d}{dx} \right)({{\Delta }_{1}})={{\Delta }_{2}}\]
done
clear
View Answer play_arrow
question_answer 306) If A is a square matrix of order 3, then\[|adj\,A|\]is equal to:
A)
\[1\]
done
clear
B)
\[|A|\]
done
clear
C)
\[|A{{|}^{3}}\]
done
clear
D)
\[|A{{|}^{2}}\]
done
clear
E)
\[|A{{|}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 307) If \[A=\left[ \begin{matrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \\ \end{matrix} \right],\]then\[{{A}^{3}}\]is equal to:
A)
\[\left[ \begin{matrix} \cos 3\theta & \sin 3\theta \\ \sin 3\theta & \cos 3\theta \\ \end{matrix} \right]\]
done
clear
B)
\[\left[ \begin{matrix} \cos 3\theta & -\sin 3\theta \\ \sin 3\theta & \cos 3\theta \\ \end{matrix} \right]\]
done
clear
C)
\[\left[ \begin{matrix} \cos 3\theta & \sin 3\theta \\ -\sin 3\theta & -\cos 3\theta \\ \end{matrix} \right]\]
done
clear
D)
\[\left[ \begin{matrix} -\cos 3\theta & -\sin 3\theta \\ -\sin 3\theta & -\cos 3\theta \\ \end{matrix} \right]\]
done
clear
E)
\[\left[ \begin{matrix} {{\cos }^{3}}\theta & {{\sin }^{3}}\theta \\ -{{\sin }^{3}}\theta & {{\cos }^{3}}\theta \\ \end{matrix} \right]\]
done
clear
View Answer play_arrow
question_answer 308) The system\[x+4y-2z=3,\,\]\[3x+y+5z=7,\] \[2x+3y+z=5\]has:
A)
infinite number of solutions
done
clear
B)
unique solution
done
clear
C)
trivial solution
done
clear
D)
no solution
done
clear
E)
multiple solutions
done
clear
View Answer play_arrow
question_answer 309) The centroid of the triangle with vertices \[A(-36,7),\text{ }B(20,7),\text{ }C(0,-8),\]is equal to:
A)
\[\left( \frac{16}{3},\frac{6}{3} \right)\]
done
clear
B)
\[\left( \frac{13}{3},\frac{6}{3} \right)\]
done
clear
C)
\[\left( 16,\frac{16}{3} \right)\]
done
clear
D)
\[\left( -\frac{16}{3},\frac{6}{3} \right)\]
done
clear
E)
None of these
done
clear
View Answer play_arrow
question_answer 310) If\[x>0\]and\[A=(-3,4),B=(-1,-2),\]\[C=(5,6),D=(x,-4)\]are the vertices of a quadrilateral such that \[\Delta ABD=2\Delta ACD,\]then the value of\[x\]is:
A)
6
done
clear
B)
9
done
clear
C)
69
done
clear
D)
96
done
clear
E)
3
done
clear
View Answer play_arrow
question_answer 311) If the three points\[(k,2k),(2k,3k),(3,1)\]are collinear, then k is equal to:
A)
2
done
clear
B)
1
done
clear
C)
\[\frac{1}{2}\]
done
clear
D)
\[-\frac{1}{2}\]
done
clear
E)
\[-2\]
done
clear
View Answer play_arrow
question_answer 312) The foot of the perpendicular from the point (3, 4) on the line\[3x-4y+5=0\]is:
A)
\[\left( \frac{81}{25},\frac{92}{25} \right)\]
done
clear
B)
\[\left( \frac{92}{25},\frac{81}{25} \right)\]
done
clear
C)
\[\left( \frac{46}{25},\frac{54}{25} \right)\]
done
clear
D)
\[\left( \frac{-81}{25},\frac{-92}{25} \right)\]
done
clear
E)
\[\left( \frac{81}{25},\frac{108}{25} \right)\]
done
clear
View Answer play_arrow