question_answer 1) A body of mass 2 kg makes an elastic collision with another body at rest and continues to move in the original direction with one-fourth its original speed. The mass of the second body which collides with the first body is:
A)
2 kg
done
clear
B)
1.2 kg
done
clear
C)
3 kg
done
clear
D)
1.5 kg
done
clear
E)
1 kg
done
clear
View Answer play_arrow
question_answer 2) In the stable equilibrium position, a body has:
A)
maximum potential energy
done
clear
B)
minimum potential energy
done
clear
C)
minimum kinetic energy
done
clear
D)
neither maximum nor minimum potential energy
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 3) A particle of mass m at rest is acted upon by a force P for a time t. Its kinetic energy after an interval t is:
A)
\[\frac{{{p}^{2}}{{t}^{2}}}{m}\]
done
clear
B)
\[\frac{{{p}^{2}}{{t}^{2}}}{2m}\]
done
clear
C)
\[\frac{{{p}^{2}}{{t}^{2}}}{3m}\]
done
clear
D)
\[\frac{pt}{2m}\]
done
clear
E)
\[\frac{p{{t}^{2}}}{2m}\]
done
clear
View Answer play_arrow
question_answer 4) A car of mass 1000 kg accelerates uniformly from rest to a velocity of 54 km/h in 5 s. The average power of the engine during this period in watts is (neglect friction):
A)
2000 W
done
clear
B)
22500 W
done
clear
C)
5000 W
done
clear
D)
2250 W
done
clear
E)
1000 W
done
clear
View Answer play_arrow
question_answer 5) A quarter horse power motor runs at a speed of 600 rpm. Assuming 40% efficiency the work done by the motor in one rotation will be:
A)
7.46 J
done
clear
B)
7400 J
done
clear
C)
7.46 erg
done
clear
D)
74.6 J
done
clear
E)
746 J
done
clear
View Answer play_arrow
question_answer 6) In the\[HCl\]molecule, the separation between the nuclei of the two atoms is about \[1.27\overset{\text{o}}{\mathop{\text{A}}}\,\] \[(1\overset{\text{o}}{\mathop{\text{A}}}\,={{10}^{-10}})\]. The approximate location of the centre of mass of the molecule, assuming the chlorine atom to be about 35.5 times as massive as hydrogen is:
A)
\[1\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
B)
\[2.5\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
C)
\[1.24\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
D)
\[1.5\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
E)
\[0.9\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
View Answer play_arrow
question_answer 7) A sphere of mass 10 kg and radius 0.5 m rotates about a tangent. The moment of inertia of the sphere is:
A)
\[5kg-{{m}^{2}}\]
done
clear
B)
\[2.7kg-{{m}^{2}}\]
done
clear
C)
\[3.5kg-{{m}^{2}}\]
done
clear
D)
\[4.5\text{ }kg-{{m}^{2}}\]
done
clear
E)
\[4kg-{{m}^{2}}\]
done
clear
View Answer play_arrow
question_answer 8) A solid sphere (mass 2 m) and a thin spherical shell (mass M) both of the same size, roll down an inclined plane, then:
A)
solid sphere will reach the bottom first
done
clear
B)
hollow spherical shell will reach the bottom first
done
clear
C)
both will reach at the same time
done
clear
D)
cannot be predicted as the data is insufficient
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 9) If the earth were to suddenly contract to half the present radius (without any external torque acting on it), by how much would the day be decreased? (Assume earth to be a perfect solid sphere of moment of inertia\[\frac{2}{5}M{{R}^{2}}\])
A)
\[8\,h\]
done
clear
B)
\[6\,h\]
done
clear
C)
\[4\,h\]
done
clear
D)
\[2\,h\]
done
clear
E)
\[1\,h\]
done
clear
View Answer play_arrow
question_answer 10) A research satellite of mass 200 kg circles the earth in an orbit of average radius 3R/2, where R is the radius of the earth. Assuming the gravitational pull on a mass of 1 kg on the earths surface to be 10 N, the pull on the satellite will be:
A)
880 N
done
clear
B)
889 N
done
clear
C)
890 N
done
clear
D)
892 N
done
clear
E)
885 N
done
clear
View Answer play_arrow
question_answer 11) If M = Mass, L = Length, T= Time and\[I=\]Electric current, then the dimensional formula for electrical resistance R is given by:
A)
\[[R]=[{{M}^{1}}{{L}^{2}}{{T}^{-3}}{{I}^{-2}}]\]
done
clear
B)
\[[R]=[{{M}^{1}}{{L}^{2}}{{T}^{-3}}{{I}^{2}}]\]
done
clear
C)
\[[R]=[{{M}^{1}}{{L}^{2}}{{T}^{3}}{{I}^{-2}}]\]
done
clear
D)
\[[R]=[{{M}^{1}}{{L}^{2}}{{T}^{3}}{{I}^{2}}]\]
done
clear
E)
\[[R]=[{{M}^{-1}}{{L}^{2}}{{T}^{-3}}{{I}^{-2}}]\]
done
clear
View Answer play_arrow
question_answer 12) A body is moving at a speed near\[0.3\text{ }m{{s}^{-1}}\]. To measure its speed with an accuracy about 1%, using a sampling distance 3 mm, the measuring clock should have a least count of the order of:
A)
0.1 s
done
clear
B)
0.01 s
done
clear
C)
0.001 s
done
clear
D)
0.0001 s
done
clear
E)
0.015 s
done
clear
View Answer play_arrow
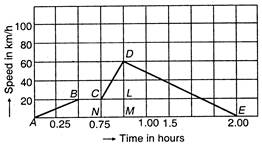
question_answer 13)
A train moves from one station to another in 2 hours time. Its speed-time graph during this motion is shown below. The maximum acceleration during the journey is:
A)
\[140\,km{{h}^{-2}}\]
done
clear
B)
\[160\,km{{h}^{-2}}\]
done
clear
C)
\[100\,km{{h}^{-2}}\]
done
clear
D)
\[120\,km{{h}^{-2}}\]
done
clear
E)
\[150\,km{{h}^{-2}}\]
done
clear
View Answer play_arrow
question_answer 14) A body dropped from a height h with an initial speed zero reaches the ground with a velocity of 3 km/h. Another body of the same mass was dropped from the same height h with an initial speed 4 km/h will reach the ground with a velocity of:
A)
3 km/h
done
clear
B)
4 km/h
done
clear
C)
5 km/h
done
clear
D)
12 km/h
done
clear
E)
8 km/h
done
clear
View Answer play_arrow
question_answer 15) If the acceleration due to gravity is\[10\text{ }m{{s}^{-2}}\]and the units of length and time are changed to kilometre and hour respectively, the numerical value of the acceleration due to gravity is:
A)
360000
done
clear
B)
72000
done
clear
C)
36000
done
clear
D)
129600
done
clear
E)
73000
done
clear
View Answer play_arrow
question_answer 16) A boat man can row with a speed of 10 km/h in still water. If the river flows at 5 km/h, the direction in which the boat man should row to reach a point on the other bank directly opposite to the point from where he started is (width of the river is 2 km):
A)
in a direction inclined at\[120{}^\circ \]to the direction of river flow
done
clear
B)
in a direction inclined at\[90{}^\circ \]to the direction of river flow
done
clear
C)
\[60{}^\circ \]in the north-west direction
done
clear
D)
should row directly along the river flow
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 17) The maximum and minimum magnitudes of the resultant of two given vectors are 17 units and 7 units respectively. If these two vectors are at right angles to each other, the magnitude of their resultant is:
A)
14
done
clear
B)
16
done
clear
C)
18
done
clear
D)
13
done
clear
E)
12
done
clear
View Answer play_arrow
question_answer 18) A cricketer can throw a ball to a maximum horizontal distance of 100 m. The speed with which he throws the ball is (to the nearest integer):
A)
\[30\text{ }m{{s}^{-1}}\]
done
clear
B)
\[\text{42 }m{{s}^{-1}}\]
done
clear
C)
\[32\text{ }m{{s}^{-1}}\]
done
clear
D)
\[\text{35 }m{{s}^{-1}}\]
done
clear
E)
\[\text{40 }m{{s}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 19) A box whose mass is 5 kg lies on a spring balance inside a lift. The lift starts to ascend with an acceleration of\[2\text{ }m{{s}^{-2}}\]. The reading of the machine or balance is\[(g=10\,m{{s}^{-2}})\]:
A)
50 kg
done
clear
B)
zero
done
clear
C)
49 kg
done
clear
D)
60 kg
done
clear
E)
45 kg
done
clear
View Answer play_arrow
question_answer 20) A ball of mass 0.5 kg moving with a velocity of \[2\text{ }m{{s}^{-1}}\]strikes a wall normally and bounces back with the same speed. If the time of contact between the ball and wall is\[{{10}^{-3}}s,\] the average force exerted by the wall on the ball is:
A)
1125N
done
clear
B)
1000 N
done
clear
C)
500 N
done
clear
D)
2000 N
done
clear
E)
5000 N
done
clear
View Answer play_arrow
question_answer 21) A telescope has an objective of focal length 50 cm and an eye-piece of focal length 5 cm. The least distance of distinct vision is 25 cm. The telescope is focussed for distinct vision on a scale 200 cm away. The separation between the objective and the eye-piece is:
A)
75 cm
done
clear
B)
60 cm
done
clear
C)
71 cm
done
clear
D)
74 cm
done
clear
E)
65 cm
done
clear
View Answer play_arrow
question_answer 22) The colour of the +ve column in a gas discharge tube depends on:
A)
the type of glass used to construct the tube
done
clear
B)
the gas in the tube
done
clear
C)
the applied voltage
done
clear
D)
the material of the cathode
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 23) Cathode rays are produced when the pressure is of the order of:
A)
2 cm of Hg
done
clear
B)
0.1 cm of Hg
done
clear
C)
0.01 mm of Hg
done
clear
D)
1 u m of Hg
done
clear
E)
0.001 mm of Hg
done
clear
View Answer play_arrow
question_answer 24) A radio transmitter radiates 1 kW power at a wavelength 198.6 m. How many photons does it emit per second?
A)
\[{{10}^{10}}\]
done
clear
B)
\[{{10}^{20}}\]
done
clear
C)
\[{{10}^{30}}\]
done
clear
D)
\[{{10}^{40}}\]
done
clear
E)
\[{{10}^{50}}\]
done
clear
View Answer play_arrow
question_answer 25) Consider the spectral line resulting from the transition from\[n=2\]to\[n=1,\]in atoms and ions given below. The shortest wavelength is produced by:
A)
hydrogen atom
done
clear
B)
deuterium atom
done
clear
C)
singly ionized helium
done
clear
D)
doubly ionized helium
done
clear
E)
doubly ionized lithium
done
clear
View Answer play_arrow
question_answer 26) The energy of an electron in excited hydrogen atom is\[-\,3.4\text{ }eV\]. Then according to Bohrs theory, the angular momentum of the electron is:
A)
\[2.1\times {{10}^{-34}}J-s\]
done
clear
B)
\[3\times {{10}^{-34}}J-s\]
done
clear
C)
\[2\times {{10}^{-34}}J-s\]
done
clear
D)
\[0.5\times {{10}^{-34}}J-s\]
done
clear
E)
\[1\times {{10}^{-34}}J-s\]
done
clear
View Answer play_arrow
question_answer 27) If the speed of light were 2/3 of its present value, the energy released in a given atomic explosion would:
A)
decrease by a factor 2/3
done
clear
B)
decrease by a factor 4/9
done
clear
C)
decrease by a factor 5/9
done
clear
D)
decrease by a factor\[\sqrt{5}/9\]
done
clear
E)
increase by a factor 2/3
done
clear
View Answer play_arrow
question_answer 28) A semiconductor has an electron concentration of\[8\times {{10}^{13}}/{{m}^{3}}\]and hole concentration of\[5.5\times {{10}^{12}}/{{m}^{3}}\]. The semiconductor is:
A)
n-type
done
clear
B)
p-type
done
clear
C)
intrinsic semiconductor
done
clear
D)
p-n junction
done
clear
E)
none of the above
done
clear
View Answer play_arrow
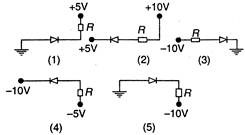
question_answer 29)
In the figure shown below, which of the diodes are forward biased?
A)
1, 2, 3
done
clear
B)
2, 4, 5
done
clear
C)
1, 3, 4
done
clear
D)
2, 3, 4
done
clear
E)
1, 4, 5
done
clear
View Answer play_arrow
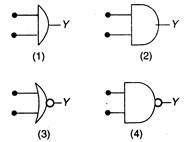
question_answer 30)
Given below are four logic gate symbols. Those for OR, NOR and NAND are respectively:
A)
1, 4, 3
done
clear
B)
4, 1, 2
done
clear
C)
1, 3, 4
done
clear
D)
4, 2, 1
done
clear
E)
3, 2, 1
done
clear
View Answer play_arrow
question_answer 31) The albedo of a planet is indicative of its:
A)
transmission coefficient
done
clear
B)
reflection coefficient
done
clear
C)
absorption coefficient
done
clear
D)
adsorption coefficient
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 32) Mass of the earth has been determined through:
A)
use of Keplers\[{{T}^{2}}/{{R}^{3}}\]constancy law
done
clear
B)
sampling the density of earths crust and using R
done
clear
C)
Cavendishs determination of G and using R and g at surface
done
clear
D)
use of periods of satellites at different heights above earths surface
done
clear
E)
it is impossible to determine
done
clear
View Answer play_arrow
question_answer 33) If 96500 C of electricity liberates\[1\,g\]equivalent of any substance, the time taken for a current of 0.15A to deposit 20 mg of copper from a solution of copper sulphate is (chemical equivalent of copper = 32):
A)
5 min 20 s
done
clear
B)
6 min 42 s
done
clear
C)
4 min 40 s
done
clear
D)
5 min 50 s
done
clear
E)
6 min
done
clear
View Answer play_arrow
question_answer 34) An electric motor operates on a 50 V supply and a current of 12 A. If the efficiency of the motor is 30%, what is the resistance of the winding of the motor?
A)
\[6\,\Omega \]
done
clear
B)
\[4\,\Omega \]
done
clear
C)
\[2.9\,\Omega \]
done
clear
D)
\[3.1\,\Omega \]
done
clear
E)
\[2.5\,\Omega \]
done
clear
View Answer play_arrow
question_answer 35)
Two long straight wires are set parallel to each other. Each carries a current in the same direction and the separation between them is 2 r. The intensity of the magnetic field mid-way between them is:
A)
\[\frac{{{\mu }_{0}}i}{r}\]
done
clear
B)
\[\frac{4{{\mu }_{0}}i}{r}\]
done
clear
C)
zero
done
clear
D)
\[\frac{{{\mu }_{0}}i}{4r}\]
done
clear
E)
\[\frac{{{\mu }_{0}}i}{2r}\]
done
clear
View Answer play_arrow
question_answer 36) A galvanometer of resistance \[20\,\Omega \] is to be converted into an ammeter of range 1A. If a current of 1 mA produces full scale deflection, the shunt required for the purpose is:
A)
\[0.01\,\Omega \]
done
clear
B)
\[0.05\,\Omega \]
done
clear
C)
\[0.02\,\Omega \]
done
clear
D)
\[0.04\Omega \]
done
clear
E)
\[0.03\Omega \]
done
clear
View Answer play_arrow
question_answer 37) There are three voltmeters of the same range but of resistance\[10000\text{ }\Omega ,\text{ }8000\text{ }\Omega \]and\[40000\text{ }\Omega \]respectively. The best voltmeter among these is the one whose resistance is:
A)
\[10000\text{ }\Omega \]
done
clear
B)
\[8000\text{ }\Omega \]
done
clear
C)
\[4000\text{ }\Omega \]
done
clear
D)
all are equally good
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 38) A magnetic needle is kept in a non-uniform magnetic field. It experiences:
A)
force and torque
done
clear
B)
a force but not a torque
done
clear
C)
a torque but not a force
done
clear
D)
neither a force nor a torque
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 39) A small rod of bismuth is suspended freely between the poles of a strong electromagnet. It is found to arrange itself at right angles to the magnetic field. This observation establishes that bismuth is:
A)
diamagnetic
done
clear
B)
paramagnetic
done
clear
C)
ferro-magnetic
done
clear
D)
anti ferro-magnetic
done
clear
E)
ferri-magnetic
done
clear
View Answer play_arrow
question_answer 40) Alternating current is transmitted to distant places:
A)
at high voltage and low current
done
clear
B)
at high voltage and high current
done
clear
C)
at low voltage and low current
done
clear
D)
at low voltage and high current
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 41) In a step-up transformer the voltage in the primary is 220 V and the current is 5 A. The secondary voltage is found to be 22000 V. The current in the secondary (neglect losses) is:
A)
5 A
done
clear
B)
50 A
done
clear
C)
500 A
done
clear
D)
0.05 A
done
clear
E)
0.5 A
done
clear
View Answer play_arrow
question_answer 42) In a pure inductive circuit, current:
A)
lags behind emf by\[\pi /2\]
done
clear
B)
leads the emf by\[\pi /2\]
done
clear
C)
lags behind by \[\pi \]
done
clear
D)
leads the emf by\[\pi \]
done
clear
E)
lags behind the emf by \[\pi /4\]
done
clear
View Answer play_arrow
question_answer 43) Two circuits have mutual inductance of 0.1 H. What average emf is induced in one circuit when the current in the other circuit changes from 0 to 20 A in 0.02 s?
A)
240 V
done
clear
B)
230 V
done
clear
C)
100 V
done
clear
D)
300 V
done
clear
E)
200 V
done
clear
View Answer play_arrow
question_answer 44) A micro-wave and an ultrasonic sound wave have the same wavelength. Their frequencies are in the ratio (approximately):
A)
\[{{10}^{6}}:1\]
done
clear
B)
\[{{10}^{4}}:1\]
done
clear
C)
\[{{10}^{2}}:1\]
done
clear
D)
\[10:1\]
done
clear
E)
\[1:1\]
done
clear
View Answer play_arrow
question_answer 45) The ozone layer absorbs:
A)
infrared radiations
done
clear
B)
ultraviolet radiations
done
clear
C)
X-rays
done
clear
D)
\[\gamma \]-rays
done
clear
E)
visible light
done
clear
View Answer play_arrow
question_answer 46) Huygens principle of secondary wavelets may be used to:
A)
find the velocity of light in vacuum
done
clear
B)
explain the particle behaviour of light
done
clear
C)
find the new position of a wavefront
done
clear
D)
explain photoelectric effect
done
clear
E)
explain scattering of light
done
clear
View Answer play_arrow
question_answer 47) In Youngs double slit experiment, the intensity of light coming from one of the slits is double the intensity from the other slit. The ratio of the maximum intensity to the minimum intensity in the interference fringe pattern observed is:
A)
34
done
clear
B)
40
done
clear
C)
25
done
clear
D)
38
done
clear
E)
30
done
clear
View Answer play_arrow
question_answer 48) Three observers A, B, C measure the speed of light coming from a source to be\[{{v}_{A}},{{v}_{B}}\]and\[{{v}_{C}}\]. The observer A moves away from the source at the same speed. The observer B stays stationary. The surrounding space is vacuum everywhere. Then:
A)
\[{{v}_{A}}>{{v}_{B}}>{{v}_{C}}\]
done
clear
B)
\[{{v}_{A}}<{{v}_{B}}<{{v}_{C}}\]
done
clear
C)
\[{{v}_{A}}={{v}_{B}}={{v}_{C}}\]
done
clear
D)
\[{{v}_{A}}={{v}_{B}}>{{v}_{C}}\]
done
clear
E)
\[{{v}_{B}}={{v}_{C}}>{{v}_{A}}\]
done
clear
View Answer play_arrow
question_answer 49) Lumen is the unit of:
A)
luminous flux
done
clear
B)
luminosity
done
clear
C)
illuminance
done
clear
D)
quantity of light
done
clear
E)
illumination
done
clear
View Answer play_arrow
question_answer 50) A man runs towards a mirror at a speed 15 m/s. The speed of the image relative to the man is:
A)
\[15\,m{{s}^{-1}}\]
done
clear
B)
\[30\text{ }m{{s}^{-1}}\]
done
clear
C)
\[35\text{ }m{{s}^{-1}}\]
done
clear
D)
\[20\text{ }m{{s}^{-1}}\]
done
clear
E)
\[25\,m{{s}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 51) The refractive index of water is 1.33. The direction in which a man under water should look to see the setting sun is:
A)
\[49{}^\circ \]to the horizontal
done
clear
B)
\[90{}^\circ \]with the vertical
done
clear
C)
\[49{}^\circ \]to the vertical
done
clear
D)
along the horizontal
done
clear
E)
in any direction
done
clear
View Answer play_arrow
question_answer 52) The solar spectrum during a complete solar eclipse is:
A)
continuous
done
clear
B)
emission line
done
clear
C)
dark line
done
clear
D)
dark band
done
clear
E)
absorption
done
clear
View Answer play_arrow
question_answer 53) When the displacement is one-half the amplitude in SHM, the fraction of the total enersy that is potential is:
A)
\[\frac{1}{2}\]
done
clear
B)
\[\frac{3}{4}\]
done
clear
C)
\[\frac{1}{4}\]
done
clear
D)
\[\frac{1}{8}\]
done
clear
E)
\[\frac{1}{6}\]
done
clear
View Answer play_arrow
question_answer 54) When a stationary wave is formed then its frequency is:
A)
same as that of the individual waves
done
clear
B)
twice that of the individual waves
done
clear
C)
half that of the individual waves
done
clear
D)
\[\sqrt{2}\]that of the individual waves
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 55) A person carrying a whistle emitting continuously a note of 272 Hz is running towards a reflecting surface with a speed of 18 km/h. The speed of sound in air is 345\[m{{s}^{-1}}\]. The number of beats heard by him is:
A)
4
done
clear
B)
6
done
clear
C)
8
done
clear
D)
3
done
clear
E)
zero
done
clear
View Answer play_arrow
question_answer 56) The distance between charges \[5\times {{10}^{-11}}C\]and \[-2.7\times {{10}^{-11}}C\]is 0.2 m. The distance at which a third charge should be placed from 4e in order that it will not experience any force along the line joining the two charges is:
A)
0.44 m
done
clear
B)
0.65 m
done
clear
C)
0.556 m
done
clear
D)
0.350 m
done
clear
E)
0.5 m
done
clear
View Answer play_arrow
question_answer 57) Small rain drops of the same size are charged to .potential V volts each. If n such drops coalesce to form a single drop, then the potential of the bigger drop is:
A)
\[{{n}^{1/3}}V\]
done
clear
B)
\[{{n}^{2/3}}V\]
done
clear
C)
\[nV\]
done
clear
D)
\[{{n}^{3/2}}V\]
done
clear
E)
\[{{n}^{1/2}}V\]
done
clear
View Answer play_arrow
question_answer 58) A parallel plate capacitor has plate of area A and separation d. It is charged to a potential difference\[{{V}_{0}}\]. charging battery is disconnected and the plates are pulled apart to three times the initial separation. The work required to separate the plates is:
A)
\[\frac{{{\varepsilon }_{0}}AV_{0}^{2}}{3d}\]
done
clear
B)
\[\frac{{{\varepsilon }_{0}}AV_{0}^{2}}{2d}\]
done
clear
C)
\[\frac{{{\varepsilon }_{0}}AV_{0}^{2}}{4d}\]
done
clear
D)
\[\frac{{{\varepsilon }_{0}}AV_{0}^{2}}{d}\]
done
clear
E)
\[\frac{{{\varepsilon }_{0}}AV_{0}^{2}}{4d}\]
done
clear
View Answer play_arrow
question_answer 59) A small sphere is charged to a potential of 50 V and a big hollow sphere is charged to potential of 100 V. Charge will flow from the smaller sphere to the bigger one when:
A)
the smaller one is placed inside the bigger one and connected by a wire
done
clear
B)
the bigger one is placed inside the smaller one and connected by means of a wire
done
clear
C)
bigger one placed by the side of the smaller one and connected by a wire
done
clear
D)
smaller one placed by the side of the bigger one
done
clear
E)
None of the above
done
clear
View Answer play_arrow
question_answer 60)
In the circuit, the potential difference across PQ will be nearest to:
A)
9.6 V
done
clear
B)
6.6 V
done
clear
C)
4.8 V
done
clear
D)
3.2 V
done
clear
E)
2.8 V
done
clear
View Answer play_arrow
question_answer 61) A wire of length 100 cm is connected to a cell of emf 2V and negligible internal resistance. The resistance of the wire is\[3\,\Omega ,\]the additional resistance required to produce a PD of 1 mV/cm is:
A)
\[60\,\,\Omega \]
done
clear
B)
\[47\,\,\Omega \]
done
clear
C)
\[57\,\,\Omega \]
done
clear
D)
\[35\,\,\Omega \]
done
clear
E)
\[55\,\,\Omega \]
done
clear
View Answer play_arrow
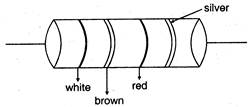
question_answer 62)
In the figure a carbon resistor has bands of different colours on its body as mentioned in the figure. The value of the resistance is:
A)
\[2.2\,\,\Omega \]
done
clear
B)
\[3.3\,\,\Omega \]
done
clear
C)
\[5.6\,\,\Omega \]
done
clear
D)
\[9.1\,\,\Omega \]
done
clear
E)
\[4.7\,\,\Omega \]
done
clear
View Answer play_arrow
question_answer 63) The period of moons rotation around the earth is nearly 29 days. If moons mass were 2 fold its present value and all other things remained unchanged, the period of moons rotation would be nearly:
A)
\[29\sqrt{2}\,days\]
done
clear
B)
\[\frac{29}{\sqrt{2}}\,days\]
done
clear
C)
\[29\times 2\,\,days\]
done
clear
D)
\[29\,\,days\]
done
clear
E)
\[\frac{29}{2}\,\,days\]
done
clear
View Answer play_arrow
question_answer 64) A uniform plank of Youngs modulus Y is moved over a smooth horizontal surface by a constant horizontal force F. The area of cross-section of the plank is A. The compressive strain on the plank in the direction of the force is:
A)
\[\frac{F}{AY}\]
done
clear
B)
\[\frac{2F}{AY}\]
done
clear
C)
\[\frac{1}{2}\frac{F}{AY}\]
done
clear
D)
\[\frac{3F}{AY}\]
done
clear
E)
\[\frac{F}{3AY}\]
done
clear
View Answer play_arrow
question_answer 65) Observers on 10th, 5th and ground floor of a tall building measure the velocity of certain rain drop by some accurate method. Surprisingly the velocity of rain drop measured by the three observers is found to be same. This is because:
A)
there is no gravitational force acting on the drop
done
clear
B)
gravitational force on the rain drop is balanced by force produced by surrounding air
done
clear
C)
gravitational force on the rain drop is balanced by upward force of attraction produced by the cloud
done
clear
D)
data is insufficient to predict
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 66) The rms speed of the molecules of a gas in a vessel is\[400\text{ }m{{s}^{-1}}\]. If half of the gas leaks out, at constant temperature, the rms speed of the remaining molecules will be:
A)
\[800\,m{{s}^{-1}}\]
done
clear
B)
\[400\sqrt{2}\,m{{s}^{-1}}\]
done
clear
C)
\[400\,m{{s}^{-1}}\]
done
clear
D)
\[200\,m{{s}^{-1}}\]
done
clear
E)
\[200\sqrt{2}\,m{{s}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 67) An electron tube was sealed off during manufacture at a pressure of\[1.2\times {{10}^{-7}}mm\]of mercury at\[27{}^\circ C\]. Its volume is 100 cm3. The number of molecules that remain in the tube is:
A)
\[2\times {{10}^{16}}\]
done
clear
B)
\[3\times {{10}^{15}}\]
done
clear
C)
\[3.86\times {{10}^{11}}\]
done
clear
D)
\[5\times {{10}^{11}}\]
done
clear
E)
\[2.5\times {{10}^{12}}\]
done
clear
View Answer play_arrow
question_answer 68) A liquid wets a solid completely. The meniscus of the liquid in a sufficiently long tube is:
A)
flat
done
clear
B)
concave
done
clear
C)
convex
done
clear
D)
cylindrical
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 69) A steel scale is to be prepared such that the millimetre intervals are to be accurate within\[6\times {{10}^{-5}}mm\]. The maximum temperature variation during the ruling of the millimeter marks is\[(a=12\times {{10}^{-6}}/{}^\circ C)\]:
A)
\[4.0{}^\circ C\]
done
clear
B)
\[4.5{}^\circ C\]
done
clear
C)
\[5.0{}^\circ C\]
done
clear
D)
\[3{}^\circ C\]
done
clear
E)
\[5.5{}^\circ C\]
done
clear
View Answer play_arrow
question_answer 70) A constant volume gas thermometer works on:
A)
Archimedes principle
done
clear
B)
Pascals law
done
clear
C)
Boyles law
done
clear
D)
Charles law
done
clear
E)
Newtons law
done
clear
View Answer play_arrow
question_answer 71) The rate of emission of a black body at\[0{}^\circ C\]is R, its rate of emission at\[273{}^\circ C\]is:
A)
4R
done
clear
B)
8R
done
clear
C)
16 R
done
clear
D)
32 R
done
clear
E)
10 R
done
clear
View Answer play_arrow
question_answer 72) The equation of a simple harmonic motion is \[X=0.34\cos (3000t+0.74),\]where X and t are in mm and sec respectively. The frequency of the motion in Hz is:
A)
\[3000\]
done
clear
B)
\[\frac{3000}{2\pi }\]
done
clear
C)
\[\frac{0.74}{2\pi }\]
done
clear
D)
\[\frac{3000}{\pi }\]
done
clear
E)
\[\frac{3000}{t}\]
done
clear
View Answer play_arrow
question_answer 73) The unit of specific conductivity is:
A)
\[\Omega \,c{{m}^{-1}}\]
done
clear
B)
\[\Omega \,c{{m}^{-2}}\]
done
clear
C)
\[{{\Omega }^{-1}}\,cm\]
done
clear
D)
\[\Omega \,c{{m}^{-3}}\]
done
clear
E)
\[{{\Omega }^{-1}}\,c{{m}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 74) The rate of a reaction is doubled for every\[10{}^\circ \]rise in temperature. The increase in reaction rate as a result of temperature rise from\[10{}^\circ \]to\[100{}^\circ \]is:
A)
112
done
clear
B)
512
done
clear
C)
400
done
clear
D)
614
done
clear
E)
100
done
clear
View Answer play_arrow
question_answer 75) The first artificial disintegration of an atomic nucleus was achieved by:
A)
Geiger
done
clear
B)
Wilson
done
clear
C)
Madam Curie
done
clear
D)
Rutherford
done
clear
E)
Soddy
done
clear
View Answer play_arrow
question_answer 76) When a beam of light is passed through a colloidal solution it:
A)
is reflected
done
clear
B)
is scattered
done
clear
C)
transmitted
done
clear
D)
absorbed
done
clear
E)
refracted
done
clear
View Answer play_arrow
question_answer 77) An important industrial solvent, also a laboratory reagent called 2-butanone is nothing but:
A)
methyl ethyl ketone
done
clear
B)
dimethyl ketone
done
clear
C)
diethyl ketone
done
clear
D)
propyi ketone
done
clear
E)
methyl propyi ketone
done
clear
View Answer play_arrow
question_answer 78) Lassaignes test is used to detect:
A)
nitrogen and halogens
done
clear
B)
sodium and halogens
done
clear
C)
halogens and sulphur
done
clear
D)
nitrogen and sulphur
done
clear
E)
nitrogen, sulphur and halogens
done
clear
View Answer play_arrow
question_answer 79) The number of possible structural isomers of butene are:
A)
3
done
clear
B)
2
done
clear
C)
4
done
clear
D)
5
done
clear
E)
1
done
clear
View Answer play_arrow
question_answer 80) Disymmetric object is one which is:
A)
superimposable on its mirror image
done
clear
B)
non-superimposable on its mirror image
done
clear
C)
optically inactive
done
clear
D)
achiral
done
clear
View Answer play_arrow
question_answer 81) Cycloalkane has the formula:
A)
\[{{C}_{n}}{{H}_{2n+2}}\]
done
clear
B)
\[{{C}_{n}}{{H}_{2n-2}}\]
done
clear
C)
\[{{C}_{n}}{{H}_{2n}}\]
done
clear
D)
\[{{C}_{2n}}{{H}_{2}}\]
done
clear
E)
\[{{C}_{2n}}{{H}_{2n}}\]
done
clear
View Answer play_arrow
question_answer 82) Three fused benzene rings are found in:
A)
naphthalene
done
clear
B)
anthracene
done
clear
C)
phenanthroline
done
clear
D)
triphenyl methane
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 83) To differentiate between carbon-12, carbon-13 and carbon-14, the instrument that you would use is:
A)
infra-red spectrometer
done
clear
B)
atomic absorption spectrometer
done
clear
C)
mass spectrometer
done
clear
D)
ultraviolet spectrometer
done
clear
E)
calorimeter
done
clear
View Answer play_arrow
question_answer 84) Irrespective of the source, pure sample of water always yields 88.89% mass of oxygen and 11.11% mass of hydrogen. This is explained by the law of:
A)
conservation of mass
done
clear
B)
constant composition
done
clear
C)
multiple proportion
done
clear
D)
constant volume
done
clear
E)
Gay-Lussac
done
clear
View Answer play_arrow
question_answer 85) A mixture of sand and iodine can be separated by:
A)
crystallisation
done
clear
B)
sublimation
done
clear
C)
distillation
done
clear
D)
fractionation
done
clear
E)
filtration
done
clear
View Answer play_arrow
question_answer 86) When the product of pressure and volume is plotted against pressure for a given amount of gas, the line obtained is:
A)
parallel to X-axis
done
clear
B)
parallel to Y-axis
done
clear
C)
linear with positive slope
done
clear
D)
linear with negative slope
done
clear
E)
either (a) or (c)
done
clear
View Answer play_arrow
question_answer 87) 32 g of\[{{O}_{2}}\], 2g of\[{{H}_{2}}\]and 28g of\[{{N}_{3}}\]at STP, occupy separately a volume of:
A)
1 L
done
clear
B)
2 L
done
clear
C)
22.4 L
done
clear
D)
2.24 L
done
clear
E)
0.224 L
done
clear
View Answer play_arrow
question_answer 88) Air at sea level is dense. This is a practical implimentation of:
A)
Boyles law
done
clear
B)
Charles law
done
clear
C)
Avogadros law
done
clear
D)
Daltons law
done
clear
E)
Gay-Lussac law
done
clear
View Answer play_arrow
question_answer 89) The electron affinity values for the halogens show the following trend:
A)
\[F<Cl>Br>I\]
done
clear
B)
\[F<Cl<Br<I\]
done
clear
C)
\[F>Cl>Br>I\]
done
clear
D)
\[F<Cl>Br<I\]
done
clear
E)
\[F>Cl<Br>I\]
done
clear
View Answer play_arrow
question_answer 90) Acetylene molecule has carbon in:
A)
sp -hybridization
done
clear
B)
\[s{{p}^{2}}-\]hybridization
done
clear
C)
\[s{{p}^{3}}-\]hybridization
done
clear
D)
\[s{{p}^{3}}d-\]hybridization
done
clear
E)
\[s{{p}^{3}}{{d}^{2}}-\]hybridization
done
clear
View Answer play_arrow
question_answer 91) When \[{{H}_{2}}S\] gas is passed through nitric acid, the product is:
A)
rhombic S
done
clear
B)
prismatic S (colloidal)
done
clear
C)
amorphous S
done
clear
D)
monoclinic S
done
clear
E)
plastic S
done
clear
View Answer play_arrow
question_answer 92) Pyrosilicate ion is:
A)
\[SiO_{2}^{2-}\]
done
clear
B)
\[SiO_{4}^{2-}\]
done
clear
C)
\[S{{i}_{2}}O_{4}^{6-}\]
done
clear
D)
\[SiO_{3}^{-}\]
done
clear
E)
\[S{{i}_{2}}O_{7}^{6-}\]
done
clear
View Answer play_arrow
question_answer 93) Atoms in a\[{{P}_{4}}\]molecule of white phosphorus are arranged regularly in space in which of the following way?
A)
At the corners of tetrahedron
done
clear
B)
At the corners of a cube
done
clear
C)
At the corners of a four membered ring
done
clear
D)
At the centre and corners of a equivalent triangle
done
clear
E)
At the centre and corners of a tetrahedron
done
clear
View Answer play_arrow
question_answer 94) The effective component of bleaching powder is the ............. of calcium:
A)
\[OCl_{2}^{2-}\]
done
clear
B)
\[OC{{l}^{-}}\]
done
clear
C)
\[{{O}_{2}}C{{l}^{-}}\]
done
clear
D)
\[{{O}^{2-}}\]
done
clear
E)
\[C{{l}^{-}}\]
done
clear
View Answer play_arrow
question_answer 95) The catalytic activity of the transition metals and their compounds is ascribed to:
A)
their chemical reactivity
done
clear
B)
their magnetic behaviour
done
clear
C)
their unfilled d-orbitals
done
clear
D)
their ability to adopt multiple oxidation states and their complexing ability
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 96) The compound\[ZnF{{e}_{2}}{{O}_{4}}\]is:
A)
a normal spinel compound
done
clear
B)
a inverse spinel compound
done
clear
C)
interstitial compound
done
clear
D)
covalent compound
done
clear
E)
co-ordination compound
done
clear
View Answer play_arrow
question_answer 97) The catalyst used for the polymerization of olefins is:
A)
Ziegler-Natta catalyst
done
clear
B)
Wilkinsons catalyst
done
clear
C)
Pd-catalyst
done
clear
D)
Zeises salt catalyst
done
clear
E)
Zeolite
done
clear
View Answer play_arrow
question_answer 98) Bakelite is a:
A)
urea-formaldehyde resin
done
clear
B)
phenol formaldehyde resin
done
clear
C)
polyethylene
done
clear
D)
artificial rubber
done
clear
E)
polyvinyl chloride
done
clear
View Answer play_arrow
question_answer 99) \[\alpha -\]helix is found in:
A)
DNA
done
clear
B)
RNA
done
clear
C)
lipid
done
clear
D)
carbohydrates
done
clear
E)
protein
done
clear
View Answer play_arrow
question_answer 100) Aspirin is:
A)
acetyl salicylic acid
done
clear
B)
2-methoxy benzoic acid
done
clear
C)
acetyl oxalic acid
done
clear
D)
methyl benzoic acid
done
clear
E)
ethoxy benzoic acid
done
clear
View Answer play_arrow
question_answer 101)
\[{{N}^{+}}\equiv NBF_{4}^{-}\]
A)
fluorobenzene
done
clear
B)
benzene
done
clear
C)
1, 2-difluoro benzene
done
clear
D)
1, 3-difluoro benzene
done
clear
E)
1, 4-difluoro benzene
done
clear
View Answer play_arrow
question_answer 102) Oxidation of aldehydes gives:
A)
esters
done
clear
B)
acids
done
clear
C)
ethers
done
clear
D)
alcohols
done
clear
E)
esters and acids
done
clear
View Answer play_arrow
question_answer 103) The common acid used in the manufacture of rayon and plastic is:
A)
methanoic acid
done
clear
B)
ethanoic acid
done
clear
C)
propanoic acid
done
clear
D)
butanoic acid
done
clear
E)
malonic acid
done
clear
View Answer play_arrow
question_answer 104) The compound used as an explosive is:
A)
2, 4, 6-tribromoaniline
done
clear
B)
1, 3, 5-trinkrobenzene
done
clear
C)
2, 4, 6-trichlorotoluene
done
clear
D)
1, 3, 5-trichlorobenzene
done
clear
E)
2, 4, 6-trinitrotoluene (TNT)
done
clear
View Answer play_arrow
question_answer 105) The indicator that is obtained by coupling the diazonium salt of sulphanilic acid with\[N,N-\]dimethylaniline is:
A)
phenanthroline
done
clear
B)
methyl orange
done
clear
C)
methyl red
done
clear
D)
phenolphthalein
done
clear
E)
indigo
done
clear
View Answer play_arrow
question_answer 106) High purity Si and Ge for semiconductor properties can be obtained by:
A)
calcination
done
clear
B)
roasting
done
clear
C)
zone refining
done
clear
D)
thermic process
done
clear
E)
electrolytic reduction
done
clear
View Answer play_arrow
question_answer 107) Name of the alloy of aluminium which is used in aeroplane is:
A)
duralumin
done
clear
B)
bell metal
done
clear
C)
\[\gamma \]-alloy (gamma alloy)
done
clear
D)
aluminium bronze
done
clear
E)
alumina
done
clear
View Answer play_arrow
question_answer 108) Invar, an alloy of Fe and Ni is used in watches and meter scale. Its characteristic property is:
A)
small coefficient of expansion
done
clear
B)
resistance of corrosion
done
clear
C)
hardness and elasticity
done
clear
D)
resistance to wear
done
clear
E)
magnetic nature
done
clear
View Answer play_arrow
question_answer 109) An alloy of Pb and Sn in equal proportion is called:
A)
pewter
done
clear
B)
type metal
done
clear
C)
solder
done
clear
D)
constantan
done
clear
E)
gun metal
done
clear
View Answer play_arrow
question_answer 110) Aqua-regia is obtained by mixing two different acids in the ratio:
A)
\[1\text{ }HN{{O}_{3}}:2\text{ }HCl\]
done
clear
B)
\[\text{3 }HN{{O}_{3}}:1\,HCl\]
done
clear
C)
\[\text{2 }HN{{O}_{3}}:2\text{ }HCl\]
done
clear
D)
\[\text{2 }HN{{O}_{3}}:3\,HCl\]
done
clear
E)
\[\text{1 }HN{{O}_{3}}:3\,HCl\]
done
clear
View Answer play_arrow
question_answer 111) A compound with cubic structure is made of elements A and B. A atoms are at the comers of the cube and B atoms are at the face centres. The simplest formula of the compound is:
A)
\[{{A}_{5}}B\]
done
clear
B)
\[A{{B}_{3}}\]
done
clear
C)
\[AB\]
done
clear
D)
\[A{{B}_{6}}\]
done
clear
E)
\[A{{B}_{8}}\]
done
clear
View Answer play_arrow
question_answer 112) Oxygen molecule contains:
A)
no unpaired electron
done
clear
B)
one unpaired electron
done
clear
C)
two unpaired electrons
done
clear
D)
three unpaired electrons
done
clear
E)
four unpaired electrons
done
clear
View Answer play_arrow
question_answer 113) Colligative properties are used for the determination of:
A)
molar mass
done
clear
B)
equivalent weight
done
clear
C)
arrangement of molecules
done
clear
D)
melting point and boiling point
done
clear
E)
both (a) and (b)
done
clear
View Answer play_arrow
question_answer 114) Identify the mixture that shows positive deviation from Raoults law:
A)
\[CHC{{l}_{3}}+{{(C{{H}_{3}})}_{2}}CO\]
done
clear
B)
\[{{(C{{H}_{3}})}_{2}}CO+{{C}_{6}}{{H}_{5}}NH\]
done
clear
C)
\[CHC{{l}_{3}}+{{C}_{6}}{{H}_{6}}\]
done
clear
D)
\[{{(C{{H}_{3}})}_{2}}CO+C{{S}_{2}}\]
done
clear
E)
\[{{C}_{6}}{{H}_{5}}N+C{{H}_{3}}COOH\]
done
clear
View Answer play_arrow
question_answer 115) If\[\Delta G\]for a reaction is negative, you infer that the change is:
A)
spontaneous
done
clear
B)
non-spontaneous
done
clear
C)
reversible
done
clear
D)
irreversible
done
clear
E)
equilibrium
done
clear
View Answer play_arrow
question_answer 116) The law of thermodynamics formulated by Dr. N. Nemst is:
A)
first law of thermodynamics
done
clear
B)
second law of thermodynamics
done
clear
C)
third law of thermodynamics
done
clear
D)
both (a) and (b)
done
clear
E)
both (b) and (c)
done
clear
View Answer play_arrow
question_answer 117) Which of the following will favour the reverse reaction in a chemical equilibrium?
A)
Increasing the concentration of the Reactants
done
clear
B)
Removal of at least one of the products at regular intervals
done
clear
C)
Increasing the concentration of one or more of the products
done
clear
D)
Increasing the pressure
done
clear
E)
None of the above
done
clear
View Answer play_arrow
question_answer 118) In the lime kiln, the reaction \[CaC{{O}_{3}}(s)\xrightarrow[{}]{{}}CaO(s)+C{{O}_{2}}(g)\] goes to completion because:
A)
of high temperature
done
clear
B)
\[CaO\]is more stable than\[CaC{{O}_{3}}\]
done
clear
C)
\[C{{O}_{2}}\]escapes simultaneously
done
clear
D)
\[CaO\]is not dissociated
done
clear
E)
\[C{{O}_{2}}\]is a gaseous product
done
clear
View Answer play_arrow
question_answer 119) \[{{K}_{p}}\]and\[{{K}_{c}}\]are related as:
A)
\[{{K}_{p}}={{K}_{c}}{{(RT)}^{\Delta n}}\]
done
clear
B)
\[{{K}_{c}}={{K}_{p}}{{(RT)}^{\Delta n}}\]
done
clear
C)
\[{{K}_{p}}+{{K}_{c}}={{(RT)}^{\Delta n}}\]
done
clear
D)
\[{{K}_{c}}={{K}_{c}}\]
done
clear
E)
\[{{K}_{c}}.{{K}_{c}}={{(RT)}^{\Delta n}}\]
done
clear
View Answer play_arrow
question_answer 120) \[\underset{(anode)}{\mathop{Zn(s)|}}\,Z{{n}^{2+}}(aq)||C{{u}^{2+}}\underset{(cathode)}{\mathop{(aq)|Cu}}\,(s)\]is:
A)
Weston cell
done
clear
B)
Daniel cell
done
clear
C)
Calomel cell
done
clear
D)
Faraday cell
done
clear
E)
Standard cell
done
clear
View Answer play_arrow
question_answer 121) The pH of\[0.005\text{ }M\text{ }{{H}_{2}}S{{O}_{4}}\]is:
A)
2.5
done
clear
B)
1.5
done
clear
C)
1.0
done
clear
D)
2.0
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 122) If the n th term of the geometric progression, \[5,-\frac{5}{2},\frac{5}{4},\frac{5}{8},....\]is\[\frac{5}{1024},\]then the value of n is:
A)
11
done
clear
B)
10
done
clear
C)
9
done
clear
D)
4
done
clear
E)
7
done
clear
View Answer play_arrow
question_answer 123) If a, b and c are respectively the p th, q th and r th terms of an AP, then\[\left| \begin{matrix} a & p & 1 \\ b & q & 1 \\ c & r & 1 \\ \end{matrix} \right|\]is equal to:
A)
1
done
clear
B)
\[-1\]
done
clear
C)
0
done
clear
D)
\[pqr\]
done
clear
E)
\[p+q+r\]
done
clear
View Answer play_arrow
question_answer 124) The sum of infinite terms of the geometric progression\[\frac{\sqrt{2}+1}{\sqrt{2}-1},\frac{1}{2-\sqrt{2}}=\frac{1}{2},....\]is:
A)
\[\sqrt{2}{{(\sqrt{2}+1)}^{2}}\]
done
clear
B)
\[{{(\sqrt{2}+1)}^{2}}\]
done
clear
C)
\[5\sqrt{2}\]
done
clear
D)
\[3\sqrt{2}+\sqrt{5}\]
done
clear
E)
\[0\]
done
clear
View Answer play_arrow
question_answer 125) The two geometric means between the numbers 1 and 64 are:
A)
1 and 64
done
clear
B)
4 and 16
done
clear
C)
2 and 16
done
clear
D)
8 and 16
done
clear
E)
3 and 16
done
clear
View Answer play_arrow
question_answer 126) The number of ways in which 5 boys and 3 girls be seated in a row so that each girl is between two boys, is:
A)
2880
done
clear
B)
1880
done
clear
C)
3800
done
clear
D)
2800
done
clear
E)
2000
done
clear
View Answer play_arrow
question_answer 127) If n and r are two positive integers such that \[n\ge r,\]then\[^{n}{{C}_{r-1}}{{+}^{n}}{{C}_{r}}\]is equal to:
A)
\[^{n}{{C}_{n-1}}\]
done
clear
B)
\[^{n}{{C}_{r}}\]
done
clear
C)
\[^{n-1}{{C}_{r}}\]
done
clear
D)
\[^{n+1}{{C}_{r}}\]
done
clear
E)
\[^{n-1}{{C}_{r-1}}\]
done
clear
View Answer play_arrow
question_answer 128) If\[^{43}{{C}_{r-6}}{{=}^{43}}{{C}_{3r+1}},\]then the value of r is:
A)
12
done
clear
B)
8
done
clear
C)
6
done
clear
D)
10
done
clear
E)
14
done
clear
View Answer play_arrow
question_answer 129) The number of straight lines that can be formed by joining 20 points of which 4 points are collinear, is:
A)
183
done
clear
B)
186
done
clear
C)
197
done
clear
D)
190
done
clear
E)
185
done
clear
View Answer play_arrow
question_answer 130) The number of ways in which a committee of 6 members can be formed from 8 gentlemen and 4 ladies so that the committee contains at least 3 ladies, is:
A)
252
done
clear
B)
672
done
clear
C)
444
done
clear
D)
420
done
clear
E)
250
done
clear
View Answer play_arrow
question_answer 131) If\[1+\frac{1+2}{2}+\frac{1+2+3}{3}+.....\]to n terms is S, then S is equal to:
A)
\[\frac{n(n+3)}{4}\]
done
clear
B)
\[\frac{n(n+2)}{4}\]
done
clear
C)
\[\frac{n(n+1)(n+2)}{6}\]
done
clear
D)
\[{{n}^{2}}\]
done
clear
E)
\[0\]
done
clear
View Answer play_arrow
question_answer 132) Let\[A=\{x:{{x}^{2}}-5x+6=0\},\] B={2,4},C={4, 5}, then\[A\times (B\cap C)\]is:
A)
{(2, 4), (3, 4)}
done
clear
B)
{(4, 2), (4, 3)}
done
clear
C)
{(2, 4), (3s 4), (4, 4)}
done
clear
D)
{(2, 2), (3, 3), (4, 4), (5, 5)}
done
clear
E)
null set
done
clear
View Answer play_arrow
question_answer 133) In a city 20 per cent of the population travels by car, 50 per cent travels by bus and 10 per cent travels by both car and bus. The persons travelling by car or bus is:
A)
80 per cent
done
clear
B)
40 per cent
done
clear
C)
60 per cent
done
clear
D)
70 per cent
done
clear
E)
30 per cent
done
clear
View Answer play_arrow
question_answer 134) If\[f(x)=\frac{2x+1}{3x-2},\]then\[(f\,\,o\,\,f)(2)\]is equal to:
A)
1
done
clear
B)
3
done
clear
C)
4
done
clear
D)
2
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 135) Which one of the following is a bijective function on the set of real numbers?
A)
\[2x-5\]
done
clear
B)
\[|x|\]
done
clear
C)
\[{{x}^{2}}\]
done
clear
D)
\[{{x}^{2}}+1\]
done
clear
E)
\[{{x}^{4}}-{{x}^{2}}+1\]
done
clear
View Answer play_arrow
question_answer 136) If\[f(x)=\log \frac{1+x}{1-x},\]then\[f(x)\]is:
A)
even
done
clear
B)
\[f({{x}_{1}})f({{x}_{2}})=f({{x}_{1}}+{{x}_{2}})\]
done
clear
C)
\[\frac{f({{x}_{1}})}{f({{x}_{2}})}=f({{x}_{1}}-{{x}_{2}})\]
done
clear
D)
odd
done
clear
E)
neither even nor odd
done
clear
View Answer play_arrow
question_answer 137) Let the function\[f\]be defined by\[f(x)=\frac{2x+1}{1-3x}\]Then\[{{f}^{-1}}(x)\]is:
A)
\[\frac{x-1}{3x+2}\]
done
clear
B)
\[\frac{3x+1}{x-1}\]
done
clear
C)
\[\frac{x+1}{3x-2}\]
done
clear
D)
\[\frac{2x+1}{1-3x}\]
done
clear
E)
\[\frac{1-3x}{2x+1}\]
done
clear
View Answer play_arrow
question_answer 138) If\[\sqrt{a+ib}=x+iy,\]then a possible value of\[\sqrt{a+ib}\]is:
A)
\[{{x}^{2}}+{{y}^{2}}\]
done
clear
B)
\[\sqrt{{{x}^{2}}+{{y}^{2}}}\]
done
clear
C)
\[x+iy\]
done
clear
D)
\[x-iy\]
done
clear
E)
\[\sqrt{{{x}^{2}}-{{y}^{2}}}\]
done
clear
View Answer play_arrow
question_answer 139) If\[(1+i)(1+2i)(1+3i)....(1+ni)=a+ib,\]then\[2\times 5\times 10\times .....\times (1+{{n}^{2}})\]is equal to:
A)
\[{{a}^{2}}+{{b}^{2}}\]
done
clear
B)
\[\sqrt{{{a}^{2}}+{{b}^{2}}}\]
done
clear
C)
\[\sqrt{{{a}^{2}}-{{b}^{2}}}\]
done
clear
D)
\[{{a}^{2}}-{{b}^{2}}\]
done
clear
E)
\[a+b\]
done
clear
View Answer play_arrow
question_answer 140) If\[{{i}^{2}}=-1,\]then the sum\[i+{{i}^{2}}+{{i}^{3}}+...\]upto 1000 terms is equal to:
A)
1
done
clear
B)
\[-1\]
done
clear
C)
i
done
clear
D)
\[-i\]
done
clear
E)
0
done
clear
View Answer play_arrow
question_answer 141) \[{{\left( \frac{1+\sin \theta +i\cos \theta }{1+\sin \theta -i\cos \theta } \right)}^{n}}\]is equal to:
A)
\[\cos \left( \frac{n\pi }{2}-n\theta \right)+i\sin \left( \frac{n\pi }{2}-n\theta \right)\]
done
clear
B)
\[\cos \left( \frac{n\pi }{2}+n\theta \right)+i\sin \left( \frac{n\pi }{2}+n\theta \right)\]
done
clear
C)
\[\sin \left( \frac{n\pi }{2}-n\theta \right)+i\cos \left( \frac{n\pi }{2}-n\theta \right)\]
done
clear
D)
\[\cos \left( \frac{n\pi }{2}+2n\theta \right)+i\sin \left( \frac{n\pi }{2}+2n\theta \right)\]
done
clear
E)
\[\cos n\theta +i\sin n\theta \]
done
clear
View Answer play_arrow
question_answer 142) If\[\omega \] is a non-real cube root of unity, then\[(a+b)(a+b\omega )(a+b{{\omega }^{2}})\] is equal to:
A)
\[{{a}^{3}}+{{b}^{3}}\]
done
clear
B)
\[{{a}^{3}}-{{b}^{3}}\]
done
clear
C)
\[{{a}^{2}}+{{b}^{2}}\]
done
clear
D)
\[{{a}^{2}}-{{b}^{2}}\]
done
clear
E)
0
done
clear
View Answer play_arrow
question_answer 143) If\[{{z}_{1}}\]and\[{{z}_{2}}\]are any two complex numbers, then which one of the following is true?
A)
\[|{{z}_{1}}+{{z}_{2}}|=|{{z}_{1}}|+|{{z}_{2}}|\]
done
clear
B)
\[|{{z}_{1}}-{{z}_{2}}|=|{{z}_{1}}|-|{{z}_{2}}|\]
done
clear
C)
\[|{{z}_{1}}-{{z}_{2}}|\le |{{z}_{1}}|+|{{z}_{2}}|\]
done
clear
D)
\[|{{z}_{1}}-{{z}_{2}}|\le |{{z}_{1}}|-|{{z}_{2}}|\]
done
clear
E)
\[\left| \frac{{{z}_{1}}}{{{z}_{2}}} \right|\ne \left| \frac{{{z}_{1}}}{{{z}_{2}}} \right|,\]where\[{{z}_{2}}\ne 0\]
done
clear
View Answer play_arrow
question_answer 144) If\[\alpha \]and\[\beta \]are the roots of the equation\[{{x}^{2}}+2x+4=0,\]then\[\frac{1}{{{\alpha }^{3}}}+\frac{1}{{{\beta }^{3}}}\]is equal to:
A)
\[-\frac{1}{2}\]
done
clear
B)
\[\frac{1}{2}\]
done
clear
C)
\[32\]
done
clear
D)
\[\frac{1}{32}\]
done
clear
E)
\[\frac{1}{4}\]
done
clear
View Answer play_arrow
question_answer 145) If\[{{x}^{2}}+ax+10=0\]and\[{{x}^{2}}+bx-10=0\]have a common root, then\[{{a}^{2}}-{{b}^{2}}\]is equal to:
A)
10
done
clear
B)
20
done
clear
C)
30
done
clear
D)
40
done
clear
E)
50
done
clear
View Answer play_arrow
question_answer 146) If\[2+i\]is a root of the equation \[{{x}^{3}}-5{{x}^{2}}+9x-5=0,\]then the other roots are:
A)
1 and\[2-i\]
done
clear
B)
-1 and\[3+i\]
done
clear
C)
0 and 1
done
clear
D)
-1 and\[i-2\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 147) The equation of the smallest degree with real coefficients having\[1+i\]as one of the roots, is:
A)
\[{{x}^{2}}+x+1=0\]
done
clear
B)
\[{{x}^{2}}-2x+2=0\]
done
clear
C)
\[{{x}^{2}}+2x+2=0\]
done
clear
D)
\[{{x}^{2}}+2x-2=0\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 148) The least integer k which makes the roots of the equation\[{{x}^{2}}+5x+k=0\]imaginary, is:
A)
4
done
clear
B)
5
done
clear
C)
3
done
clear
D)
7
done
clear
E)
8
done
clear
View Answer play_arrow
question_answer 149) If\[{{x}^{2}}+px+q=0\]is the quadratic equation whose roots are\[a-2\]and\[b-2\]where a and b are the roots of\[{{x}^{2}}-3x+1=0,\]then:
A)
\[p=1,q=5\]
done
clear
B)
\[p=5,q=1\]
done
clear
C)
\[p=1,q=1\]
done
clear
D)
\[p=1,q=-1\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 150) The number of terms of the AP series 3, 7, 11, 15, ... to be taken so that the sum is 406, is:
A)
5
done
clear
B)
10
done
clear
C)
12
done
clear
D)
14
done
clear
E)
20
done
clear
View Answer play_arrow
question_answer 151) If the progression 3, 10, 17, ... and 63, 65, 67,... are such that their n th term are equal, then n is equal to:
A)
13
done
clear
B)
15
done
clear
C)
9
done
clear
D)
8
done
clear
E)
11
done
clear
View Answer play_arrow
question_answer 152) A force of magnitude 5 unit acting along the vector\[2\hat{i}-2\hat{j}+\hat{k}\]displaces the point of application from (1, 2, 3) to (5, 3, 7). Then the work done is:
A)
50/7 unit
done
clear
B)
50/3 unit
done
clear
C)
25/3 unit
done
clear
D)
25/4 unit
done
clear
E)
3/50 unit
done
clear
View Answer play_arrow
question_answer 153) An unit vector perpendicular to both\[\hat{i}+\hat{j}\] and \[\hat{j}+\hat{k}\] is:
A)
\[\hat{i}-\hat{j}+\hat{k}\]
done
clear
B)
\[\hat{i}+\hat{j}+\hat{k}\]
done
clear
C)
\[\frac{\hat{i}+\hat{j}-\hat{k}}{\sqrt{3}}\]
done
clear
D)
\[\frac{\hat{i}-\hat{j}+\hat{k}}{\sqrt{3}}\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 154) The area of the triangle whose vertices are (1, 2, 3), (2, 5, -1) and (-1, 1, 2) is:
A)
150 sq unit
done
clear
B)
145 sq unit
done
clear
C)
\[\frac{\sqrt{155}}{2}\]sq unit
done
clear
D)
\[\frac{155}{2}\]sq unit
done
clear
E)
\[\frac{\sqrt{165}}{2}\]sq unit
done
clear
View Answer play_arrow
question_answer 155) For any three vectors\[\overrightarrow{a},\overrightarrow{b},\overrightarrow{c},\] \[\overrightarrow{a}\times (\overrightarrow{b}+\overrightarrow{c})+\overrightarrow{b}\times (\overrightarrow{c}+\vec{a})+\vec{c}\times (\overrightarrow{a}+\overrightarrow{b})\]is:
A)
\[\vec{0}\]
done
clear
B)
\[\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\]
done
clear
C)
\[\overrightarrow{a}.(\overrightarrow{b}\times \overrightarrow{c})\]
done
clear
D)
\[(\overrightarrow{a}\times \overrightarrow{b}).\overrightarrow{c}\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 156) The equation of the plane passing through the intersection of the planes\[x+2y+3z+4=0\] and\[4x+3y+2z+1=0\]and the origin is:
A)
\[3x+2y+z+1=0\]
done
clear
B)
\[3x+2y+z=0\]
done
clear
C)
\[2x+3y+\text{ }z=0\]
done
clear
D)
\[x+y+z=0\]
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 157) If\[\overrightarrow{a},\text{ }\overrightarrow{b},\text{ }\overrightarrow{c}\]are any three vectors, then \[[\overrightarrow{a}\,\text{+}\,\overrightarrow{b}\,\,\overrightarrow{b}\,+\,\overrightarrow{c}\,\overrightarrow{c}\,+\,\overrightarrow{a}]\] is equal to:
A)
\[[\overrightarrow{a}\,\,\overrightarrow{b}\,\,\overrightarrow{c}]\]
done
clear
B)
\[0\]
done
clear
C)
\[2[\overrightarrow{a}\,\,\overrightarrow{b}\,\,\overrightarrow{c}]\]
done
clear
D)
\[{{[\overrightarrow{a}\,\,\overrightarrow{b}\,\,\overrightarrow{c}]}^{2}}\]
done
clear
E)
\[(\overrightarrow{a}\,\times \,\overrightarrow{b})\times \,\,\overrightarrow{c}\]
done
clear
View Answer play_arrow
question_answer 158) The volume of the parallelepiped whose coterminous edges are\[\hat{i}-\hat{j}+\hat{k},2\hat{i}-4\hat{j}+5\hat{k}\] and\[3\hat{i}-5\hat{j}+2\hat{k}\]is:
A)
4 cu unit
done
clear
B)
3 cu unit
done
clear
C)
2 cu unit
done
clear
D)
1 cu unit
done
clear
E)
8 cu unit
done
clear
View Answer play_arrow
question_answer 159) If \[\left( \frac{1}{2},\,\frac{1}{3},\,n \right)\] are the direction cosines of a line, then the value of n is:
A)
\[\frac{\sqrt{23}}{6}\]
done
clear
B)
\[\frac{23}{36}\]
done
clear
C)
\[\frac{2}{3}\]
done
clear
D)
\[\frac{3}{2}\]
done
clear
E)
\[\frac{1}{6}\]
done
clear
View Answer play_arrow
question_answer 160) For any vector\[\overrightarrow{a},\hat{i}\times (\overrightarrow{a}\times \hat{i})+\hat{j}\times (\overrightarrow{a}\times \hat{j})\]\[+\hat{k}\times (\overrightarrow{a}\times \hat{k})\]is equal to:
A)
\[\overrightarrow{0}\]
done
clear
B)
\[\overrightarrow{a}\]
done
clear
C)
\[2\overrightarrow{a}\]
done
clear
D)
\[3\overrightarrow{a}\]
done
clear
E)
\[4\overrightarrow{a}\]
done
clear
View Answer play_arrow
question_answer 161) The equation of the plane passing through (2, 3, 4) and parallel to the plane \[5x-6y+7z=3\]is:
A)
\[5x-6y+7z+20=0\]
done
clear
B)
\[5x-6y+7z-20=0\]
done
clear
C)
\[5x+6y-7z+3=0\]
done
clear
D)
\[5x+6y+7z+3=0\]
done
clear
E)
\[5x+6y+7z-3=0\]
done
clear
View Answer play_arrow
question_answer 162) The first three terms in the expansion of\[{{(1+ax)}^{n}}(n\ne 0)\]are\[1,6x\]and\[16{{x}^{2}}\].Then the values of a and n are respectively:
A)
2 and 9
done
clear
B)
3 and 2
done
clear
C)
\[\frac{2}{3}\]and 9
done
clear
D)
\[\frac{3}{2}\]and 6
done
clear
E)
\[\frac{-2}{3}\] and 9
done
clear
View Answer play_arrow
question_answer 163) Value of the determinant \[\left| \begin{matrix} 1+a & 1 & 1 \\ 1 & 1+b & 1 \\ 1 & 1 & 1+c \\ \end{matrix} \right|\]is:
A)
\[1+abc+ab+bc+ca\]
done
clear
B)
\[abc\]
done
clear
C)
\[4abc\]
done
clear
D)
\[abc\left( \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right)\]
done
clear
E)
\[abc\left( 1+\frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right)\]
done
clear
View Answer play_arrow
question_answer 164) If the value of the determinant \[\left| \begin{matrix} x+1 & 1 & 1 \\ 2 & x+2 & 2 \\ 3 & 3 & x+3 \\ \end{matrix} \right|\]is equal to zero, then\[x\]is:
A)
0 and\[-6\]
done
clear
B)
0 and 6
done
clear
C)
6
done
clear
D)
\[-6\]
done
clear
E)
\[0\]
done
clear
View Answer play_arrow
question_answer 165) The value of a for which the matrix\[A=\left[ \begin{matrix} a & 2 \\ 2 & 4 \\ \end{matrix} \right]\]is singular:
A)
\[a\ne 1\]
done
clear
B)
\[a=1\]
done
clear
C)
\[a=0\]
done
clear
D)
\[a=-1\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 166) If \[A=\left[ \begin{matrix} 2 & -1 \\ -1 & 2 \\ \end{matrix} \right]\]and\[I\]is the unit matrix of order two, then\[{{A}^{2}}\]is equal to:
A)
\[4A-3I\]
done
clear
B)
\[3A-4I\]
done
clear
C)
\[A-I\]
done
clear
D)
\[A+I\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 167) If A and B are two square matrices of the same order, then\[{{(A-B)}^{2}}\]:
A)
\[{{A}^{2}}-AB-BA+{{B}^{2}}\]
done
clear
B)
\[{{A}^{2}}-2AB+{{B}^{2}}\]
done
clear
C)
\[{{A}^{2}}-2BA+{{B}^{2}}\]
done
clear
D)
\[{{A}^{2}}-{{B}^{2}}\]
done
clear
E)
\[{{A}^{2}}+{{B}^{2}}\]
done
clear
View Answer play_arrow
question_answer 168) If\[P=\left[ \begin{matrix} i & 0 & -i \\ 0 & -i & i \\ -i & i & 0 \\ \end{matrix} \right]\]and\[Q=\left[ \begin{matrix} -i & i \\ 0 & 0 \\ i & -i \\ \end{matrix} \right],\]then PQ is equal to:
A)
\[\left[ \begin{matrix} -2 & 2 \\ 1 & -1 \\ 1 & -1 \\ \end{matrix} \right]\]
done
clear
B)
\[\left[ \begin{matrix} 2 & -2 \\ -1 & 1 \\ -1 & 1 \\ \end{matrix} \right]\]
done
clear
C)
\[\left[ \begin{matrix} 2 & -2 \\ -1 & 1 \\ \end{matrix} \right]\]
done
clear
D)
\[\left[ \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right]\]
done
clear
E)
\[\left[ \begin{matrix} 1 & 0 \\ 0 & 1 \\ \end{matrix} \right]\]
done
clear
View Answer play_arrow
question_answer 169) If\[I\]is the unit matrix of order 10, then the determinant of\[\lambda \]is equal to:
A)
10
done
clear
B)
1
done
clear
C)
\[\frac{1}{10}\]
done
clear
D)
9
done
clear
E)
0
done
clear
View Answer play_arrow
question_answer 170) If the vectors\[3\hat{i}+\lambda \hat{j}+\hat{k}\]and\[2\hat{i}-\hat{j}+8\hat{k}\]are perpendicular, then\[\lambda \]is:
A)
\[-14\]
done
clear
B)
\[7\]
done
clear
C)
\[14\]
done
clear
D)
\[\frac{1}{7}\]
done
clear
E)
\[\frac{1}{14}\]
done
clear
View Answer play_arrow
question_answer 171) The projection of the vector\[\hat{i}+\hat{j}+\hat{k}\]along the vector\[\hat{j}\] is:
A)
1
done
clear
B)
0
done
clear
C)
2
done
clear
D)
\[-1\]
done
clear
E)
\[-2\]
done
clear
View Answer play_arrow
question_answer 172) \[\underset{x\to 0}{\mathop{\lim }}\,\frac{1-\cos mx}{1-\cos mx}\]is equal to:
A)
\[\frac{m}{n}\]
done
clear
B)
\[\frac{{{m}^{2}}}{{{n}^{2}}}\]
done
clear
C)
\[0\]
done
clear
D)
\[\frac{{{n}^{2}}}{{{m}^{2}}}\]
done
clear
E)
\[\frac{n}{m}\]
done
clear
View Answer play_arrow
question_answer 173) Which of the following is not true?
A)
a polynomial function is always continuous
done
clear
B)
a continuous function is always differentiable
done
clear
C)
a differentiable function is always continuous
done
clear
D)
\[{{e}^{x}}\]is continuous for all\[x\]
done
clear
E)
\[log\text{ }x\]is continuous for all\[x\]greater than zero
done
clear
View Answer play_arrow
question_answer 174) \[\underset{x\to 0}{\mathop{\lim }}\,\frac{{{a}^{x}}-{{b}^{x}}}{{{e}^{x}}-1}\]is equal to:
A)
\[\log \frac{a}{b}\]
done
clear
B)
\[\log \frac{b}{a}\]
done
clear
C)
\[\log ab\]
done
clear
D)
\[\log (a+b)\]
done
clear
E)
0
done
clear
View Answer play_arrow
question_answer 175) The derivative of\[{{x}^{6}}+{{6}^{x}}\]with respect to\[x\]is:
A)
\[12x\]
done
clear
B)
\[x+4\]
done
clear
C)
\[6{{x}^{5}}+{{6}^{x}}log\text{ }6\]
done
clear
D)
\[6{{x}^{5}}+{{x}^{{{6}^{x-1}}}}\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 176) If\[x=a\text{ }co{{s}^{4}}\theta ,\text{ }y=a\text{ }si{{n}^{4}}\theta ,\]then y at \[\theta =\frac{3\pi }{4}\]is:
A)
\[{{a}^{2}}\]
done
clear
B)
1
done
clear
C)
\[-1\]
done
clear
D)
\[-{{a}^{2}}\]
done
clear
E)
\[\pi \]
done
clear
View Answer play_arrow
question_answer 177) If\[\sin y+{{e}^{-x\cos y}}=e,\]then\[\frac{dy}{dx}\]at\[(1,\pi )\]is:
A)
\[\sin y\]
done
clear
B)
\[-x\cos y\]
done
clear
C)
\[e\]
done
clear
D)
\[\sin y-x\cos y\]
done
clear
E)
\[\sin y+x\cos y\]
done
clear
View Answer play_arrow
question_answer 178) If\[x={{\sin }^{-1}}(3t-4{{t}^{3}})\]and\[y={{\cos }^{-1}}(\sqrt{1-{{t}^{2}}}),\]then\[\frac{dy}{dx}\]is equal to:
A)
\[\frac{1}{3}\]
done
clear
B)
\[\frac{2}{5}\]
done
clear
C)
\[\frac{3}{2}\]
done
clear
D)
\[\frac{2}{3}\]
done
clear
E)
\[0\]
done
clear
View Answer play_arrow
question_answer 179) The second derivative of\[a{{\sin }^{3}}t\]with respect to\[a{{\cos }^{3}}t\]at\[t=\frac{\pi }{4}\]is:
A)
\[\frac{4\sqrt{2}}{3a}\]
done
clear
B)
\[2\]
done
clear
C)
\[\frac{1}{12a}\]
done
clear
D)
\[0\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 180) The equation of the tangent to the curve \[(1+{{x}^{2}})y=2-x\]where it crosses the\[x-\]axis, is:
A)
\[x+5y=2\]
done
clear
B)
\[x-5y=2\]
done
clear
C)
\[5x-y=2\]
done
clear
D)
\[5x+y-2=0\]
done
clear
E)
\[x-5y=0\]
done
clear
View Answer play_arrow
question_answer 181) The sides of an equilateral triangle are increasing at the rate of 2 cm/s. The rate at which the area increases, when the side is 10 cm, is:
A)
\[\sqrt{3}\,sq\text{ }cm/s\]
done
clear
B)
10 sq cm/s
done
clear
C)
\[10\sqrt{3}\,sq\text{ }cm/s\]
done
clear
D)
\[\frac{10}{\sqrt{3}}\,sq\text{ }cm/s\]
done
clear
E)
\[10\sqrt{2}\,sq\text{ }cm/s\]
done
clear
View Answer play_arrow
question_answer 182) The differential equation for which\[y=a\text{ }cos\text{ }x+b\text{ }sin\text{ }x\] is a solution, is:
A)
\[\frac{{{d}^{2}}y}{d{{x}^{2}}}+y=0\]
done
clear
B)
\[\frac{{{d}^{2}}y}{d{{x}^{2}}}-y=0\]
done
clear
C)
\[\frac{{{d}^{2}}y}{d{{x}^{2}}}+(a+b)y=0\]
done
clear
D)
\[\frac{{{d}^{2}}y}{d{{x}^{2}}}=(a+b)y\]
done
clear
E)
\[\frac{{{d}^{2}}y}{d{{x}^{2}}}=(a-b)y\]
done
clear
View Answer play_arrow
question_answer 183) The solution of\[\frac{dy}{dx}+p(x)y=0\]is:
A)
\[y=c{{e}^{\int{p\,dx}}}\]
done
clear
B)
\[y=c{{e}^{-\int{p\,dx}}}\]
done
clear
C)
\[x=c{{e}^{-\int{p\,dy}}}\]
done
clear
D)
\[x=c{{e}^{\int{p\,dy}}}\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 184) The differential equation of the family of lines passing through the origin is:
A)
\[x\frac{dy}{dx}+y=0\]
done
clear
B)
\[x+\frac{dy}{dx}=0\]
done
clear
C)
\[\frac{dy}{dx}=y\]
done
clear
D)
\[\frac{dy}{dx}=x\]
done
clear
E)
\[x\frac{dy}{dx}-y=0\]
done
clear
View Answer play_arrow
question_answer 185) The solution of\[\frac{dy}{dx}+y={{e}^{-x}};y(0)=0\]is:
A)
\[y={{e}^{-x}}(x-1)\]
done
clear
B)
\[y=x{{e}^{-x}}\]
done
clear
C)
\[y=x{{e}^{-x}}+1\]
done
clear
D)
\[y=(x+1){{e}^{-x}}\]
done
clear
E)
\[y=x{{e}^{x}}\]
done
clear
View Answer play_arrow
question_answer 186) A batsman scores runs in 10 innings 34, 38, 42, 46, 44, 46, 48, 54, 55, 63, 46. Then the mean deviation is:
A)
8.6
done
clear
B)
6.4
done
clear
C)
10.6
done
clear
D)
9.6
done
clear
E)
7.6
done
clear
View Answer play_arrow
question_answer 187) A coin is tossed 10 times. The probability of getting exactly 6 heads is:
A)
\[\frac{512}{105}\]
done
clear
B)
\[\frac{105}{512}\]
done
clear
C)
\[\frac{100}{513}\]
done
clear
D)
\[^{10}{{C}_{6}}\]
done
clear
E)
\[^{10}{{C}_{4}}\,\times 6!\]
done
clear
View Answer play_arrow
question_answer 188) If\[P(A)=\frac{2}{3},P(B)=\frac{1}{2}\]and\[P(A\cup B)=\frac{5}{6},\]then events A and B are:
A)
mutually exclusive
done
clear
B)
independent as well as mutually exclusive
done
clear
C)
independent
done
clear
D)
dependent only on A
done
clear
E)
dependent only on B
done
clear
View Answer play_arrow
question_answer 189)
For the data \[x\] 4 7 8 3 4 \[y\] 5 8 6 3 5
the Karl Pearson coefficient is:
A)
\[\frac{63}{\sqrt{94\times 66}}\]
done
clear
B)
\[63\]
done
clear
C)
\[\frac{63}{\sqrt{94}}\]
done
clear
D)
\[\frac{63}{\sqrt{66}}\]
done
clear
E)
\[\frac{1}{\sqrt{94\times 66}}\]
done
clear
View Answer play_arrow
question_answer 190) The average weight of students in a class of 35 students is 40 kg. If the weight of the teacher be included, the average weight rises by\[\frac{1}{2}\]kg. The weight of the teacher is:
A)
40.5 kg
done
clear
B)
50 kg
done
clear
C)
41 kg
done
clear
D)
40 kg
done
clear
E)
58 kg
done
clear
View Answer play_arrow
question_answer 191) In a bivariate data\[\Sigma x=30,\Sigma y=400,\Sigma {{x}^{2}}=196,\Sigma xy=850\]and\[n=10\]. The regression coefficient of y on \[x\]is:
A)
\[-3.1\]
done
clear
B)
\[-3.2\]
done
clear
C)
\[-3.3\]
done
clear
D)
\[-3.4\]
done
clear
E)
\[-3.5\]
done
clear
View Answer play_arrow
question_answer 192) \[\int_{-2}^{2}{|1-x{{|}^{2}}}dx\]is equal to:
A)
4
done
clear
B)
2
done
clear
C)
\[-2\]
done
clear
D)
0
done
clear
E)
1
done
clear
View Answer play_arrow
question_answer 193) \[\int{\frac{\sqrt{\tan }x}{\sin x\cos x}}dx\]is equal to:
A)
\[2\tan x+c\]
done
clear
B)
\[\sqrt{\cot x}+c\]
done
clear
C)
\[2\sqrt{\tan x}+c\]
done
clear
D)
\[{{\tan }^{2}}x+c\]
done
clear
E)
\[\cot x+c\]
done
clear
View Answer play_arrow
question_answer 194) \[\int{\frac{dx}{{{x}^{2}}+4x+13}}\]is equal to:
A)
\[\log ({{x}^{2}}+4x+130)+c\]
done
clear
B)
\[\frac{1}{3}{{\tan }^{-1}}\left( \frac{x+2}{3} \right)+c\]
done
clear
C)
\[\log (2x+4)+c\]
done
clear
D)
\[\frac{1}{{{x}^{2}}+4x+13}+c\]
done
clear
E)
\[\frac{2x+4}{{{({{x}^{2}}+4x+13)}^{2}}}+c\]
done
clear
View Answer play_arrow
question_answer 195) \[\int_{0}^{1}{\frac{d}{dx}}\left[ {{\sin }^{-1}}\left( \frac{2x}{1+{{x}^{2}}} \right) \right]dx\]is equal to:
A)
\[0\]
done
clear
B)
\[\pi \]
done
clear
C)
\[\frac{\pi }{2}\]
done
clear
D)
\[\frac{\pi }{4}\]
done
clear
E)
\[-\pi \]
done
clear
View Answer play_arrow
question_answer 196) \[\int_{0}^{\frac{\pi }{2}}{\frac{\sin x}{\sin x+\cos x}}dx\]equals to:
A)
\[\pi \]
done
clear
B)
\[\frac{\pi }{2}\]
done
clear
C)
\[\frac{\pi }{3}\]
done
clear
D)
\[\frac{\pi }{4}\]
done
clear
E)
\[\frac{\pi }{5}\]
done
clear
View Answer play_arrow
question_answer 197) The area bounded by the parabolas\[{{y}^{2}}=4ax\]and\[{{x}^{2}}=4ay\]is:
A)
\[\frac{8{{a}^{3}}}{3}sq\ unit\]
done
clear
B)
\[\frac{16{{a}^{2}}}{3}sq\ unit\]
done
clear
C)
\[\frac{32{{a}^{2}}}{3}sq\ unit\]
done
clear
D)
\[\frac{64{{a}^{2}}}{3}sq\ unit\]
done
clear
E)
\[\frac{128{{a}^{2}}}{3}sq\ unit\]
done
clear
View Answer play_arrow
question_answer 198) The area of the region\[\{(x,y):{{x}^{2}}+{{y}^{2}}\le 1\le x+y\}\]is:
A)
\[\frac{{{\pi }^{2}}}{5}sq\,unit\]
done
clear
B)
\[\frac{{{\pi }^{2}}}{2}sq\,unit\]
done
clear
C)
\[\frac{{{\pi }^{2}}}{3}sq\,unit\]
done
clear
D)
\[\frac{\pi }{4}sq\,unit\]
done
clear
E)
\[\left( \frac{\pi }{4}-\frac{1}{2} \right)sq\,unit\]
done
clear
View Answer play_arrow
question_answer 199) The area bounded by the curve\[y=sin\text{ }x\]between the ordinates \[x=0,\,\,x=\pi \] and the\[x-\]axis is:
A)
2 sq unit
done
clear
B)
4 sq unit
done
clear
C)
1 sq unit
done
clear
D)
3 sq unit
done
clear
E)
0
done
clear
View Answer play_arrow
question_answer 200) The degree of the differential equation\[\frac{{{d}^{2}}y}{d{{x}^{2}}}+{{\left( \frac{dy}{dx} \right)}^{3}}+6y=0\]is:
A)
1
done
clear
B)
3
done
clear
C)
2
done
clear
D)
5
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 201) The solution of the equation \[(2y-1)dx-(2x+3)dy=0\]is:
A)
\[\frac{2x-1}{2y+3}=c\]
done
clear
B)
\[\frac{2x+3}{2y-1}=c\]
done
clear
C)
\[\frac{2x-3}{2y-1}=c\]
done
clear
D)
\[\frac{2y+1}{2x-3}=c\]
done
clear
E)
\[\frac{2x+1}{2y-3}=c\]
done
clear
View Answer play_arrow
question_answer 202) If \[f(x)=\left\{ \begin{matrix} \frac{{{x}^{2}}-9}{x-3} \\ 2x+k \\ \end{matrix} \right.\]if \[x\ne 3\]is continuous at otherwise\[x=3,\]then k is equal to:
A)
3
done
clear
B)
0
done
clear
C)
\[-6\]
done
clear
D)
\[\frac{1}{6}\]
done
clear
E)
\[-\frac{1}{6}\]
done
clear
View Answer play_arrow
question_answer 203) The function\[f(x)=1-{{x}^{3}}-{{x}^{5}}\]is decreasing for:
A)
\[1\le x\le 5\]
done
clear
B)
\[x\le 1\]
done
clear
C)
\[x\ge 1\]
done
clear
D)
all values of\[x\]
done
clear
E)
\[0\le x\le 1\]
done
clear
View Answer play_arrow
question_answer 204) \[\frac{d}{dx}({{x}^{x}})\]is equal to:
A)
\[log\text{ }x\]
done
clear
B)
\[\log {{e}^{x}}\]
done
clear
C)
\[{{x}^{x}}log\text{ }x\]
done
clear
D)
\[{{x}^{x}}\log e\,x\]
done
clear
E)
\[{{x}^{x}}\log \text{ }(1-x)\]
done
clear
View Answer play_arrow
question_answer 205) If the displacements of a particle at time t is given by\[{{s}^{2}}=a{{t}^{2}}+2bt+c,\]then acceleration varies as:
A)
\[\frac{1}{{{s}^{2}}}\]
done
clear
B)
\[\frac{1}{s}\]
done
clear
C)
\[\frac{1}{{{s}^{3}}}\]
done
clear
D)
\[{{s}^{3}}\]
done
clear
E)
\[{{s}^{2}}\]
done
clear
View Answer play_arrow
question_answer 206) If PQ and PR are the two sides of a triangle, then the angle between them which gives maximum area of the triangle, is:
A)
\[\pi \]
done
clear
B)
\[\frac{\pi }{3}\]
done
clear
C)
\[\frac{\pi }{4}\]
done
clear
D)
\[2\pi \]
done
clear
E)
\[\frac{\pi }{2}\]
done
clear
View Answer play_arrow
question_answer 207) The function\[y=a(a-\cos x)\]is maximum when\[x\]is equal to:
A)
\[\pi \]
done
clear
B)
\[\frac{\pi }{2}\]
done
clear
C)
\[-\frac{\pi }{2}\]
done
clear
D)
\[-\frac{\pi }{6}\]
done
clear
E)
\[\frac{\pi }{3}\]
done
clear
View Answer play_arrow
question_answer 208) \[\int{\frac{\sin x}{\sin (x-\alpha )}}dx\]is equal to:
A)
\[(x-\alpha )\cos \alpha +\sin \alpha \log \sin (x-\alpha )+c\]
done
clear
B)
\[(x-\alpha )\cos x+\log \sin (x-\alpha )+c\]
done
clear
C)
\[\sin (x-\alpha )+\sin x+c\]
done
clear
D)
\[\cos (x-\alpha )+\cos x+c\]
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 209) \[\int{{{13}^{x}}}dx\]is:
A)
\[\frac{{{13}^{x}}}{\log 13}+c\]
done
clear
B)
\[{{13}^{x+1}}+c\]
done
clear
C)
\[14x+c\]
done
clear
D)
\[{{14}^{x+1}}+c\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 210) \[\int_{0}^{\frac{\pi }{2}}{\sin 2x}\log \tan x\,dx\]is equal to:
A)
\[\pi \]
done
clear
B)
\[\frac{\pi }{2}\]
done
clear
C)
1
done
clear
D)
\[2\pi \]
done
clear
E)
0
done
clear
View Answer play_arrow
question_answer 211) \[\int_{0}^{\frac{\pi }{2}}{x\sin x\,dx}\]is equal to:
A)
\[\frac{\pi }{4}\]
done
clear
B)
\[\frac{\pi }{2}\]
done
clear
C)
\[\pi \]
done
clear
D)
1
done
clear
E)
0
done
clear
View Answer play_arrow
question_answer 212) The inclination of the straight line passing through the point\[(-3,6)\]and the midpoint of the line joining the points\[(4,-5)\]and\[(-2,9)\]
A)
\[\frac{\pi }{4}\]
done
clear
B)
\[\frac{\pi }{6}\]
done
clear
C)
\[\frac{\pi }{3}\]
done
clear
D)
\[\frac{3\pi }{4}\]
done
clear
E)
\[\frac{5\pi }{6}\]
done
clear
View Answer play_arrow
question_answer 213) A point moves such that the area of the triangle formed by it with the points (1, 5) and \[(3,-7)\]is 21 sq unit. Then locus of the point is:
A)
\[6x+y-32=0\]
done
clear
B)
\[6x-y+32=0\]
done
clear
C)
\[x+6y-32=0\]
done
clear
D)
\[6x-y-32=0\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 214) The line\[\frac{x}{a}-\frac{y}{b}=1\]cuts the\[x-\]axis at P. The equation of the line through P perpendicular to the given line is:
A)
\[x+y=ab\]
done
clear
B)
\[x+y=a+b\]
done
clear
C)
\[ax+by={{a}^{2}}\]
done
clear
D)
\[bx+ay={{b}^{2}}\]
done
clear
E)
\[ax-by=ab\]
done
clear
View Answer play_arrow
question_answer 215) The value of\[\lambda \]For which the lines\[3x+4y=5,\] \[2x+3y=4\]and\[\lambda x+4y=6\]meet at a point, is:
A)
2
done
clear
B)
1
done
clear
C)
4
done
clear
D)
3
done
clear
E)
0
done
clear
View Answer play_arrow
question_answer 216) Three vertices of a parallelogram taken in order are\[(-1,-6),(2,-5)\]and (7, 2). The fourth vertex is:
A)
(1, 4)
done
clear
B)
(1, 1)
done
clear
C)
(4, 4)
done
clear
D)
(4, 1)
done
clear
E)
0
done
clear
View Answer play_arrow
question_answer 217) The orthocentre of the triangle whose vertices are\[(5,-2),(-1,2)\]and (1, 4), is:
A)
\[\left( -\frac{1}{5},\frac{16}{5} \right)\]
done
clear
B)
\[\left( \frac{14}{5},\frac{1}{5} \right)\]
done
clear
C)
\[\left( \frac{1}{5},\frac{1}{5} \right)\]
done
clear
D)
\[\left( \frac{14}{5},\frac{14}{5} \right)\]
done
clear
E)
\[(5,14)\]
done
clear
View Answer play_arrow
question_answer 218) Distance between the lines\[5x+3y-7=0\]and \[15x+9y+14=0\]is:
A)
\[\frac{35}{\sqrt{34}}\]
done
clear
B)
\[\frac{1}{3\sqrt{34}}\]
done
clear
C)
\[\frac{35}{3\sqrt{34}}\]
done
clear
D)
\[\frac{35}{2\sqrt{34}}\]
done
clear
E)
35
done
clear
View Answer play_arrow
question_answer 219) If the equation\[2{{x}^{2}}+7xy+3{{y}^{2}}-9x-7y\]\[+k=\]\[0\]represents a pair of lines, then k is equal to:
A)
4
done
clear
B)
2
done
clear
C)
1
done
clear
D)
\[-4\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 220) The angle between the lines\[2x-y+3=0\] and\[x+2y+3=0\]is:
A)
\[90{}^\circ \]
done
clear
B)
\[60{}^\circ \]
done
clear
C)
\[45{}^\circ \]
done
clear
D)
\[30{}^\circ \]
done
clear
E)
\[180{}^\circ \]
done
clear
View Answer play_arrow
question_answer 221) Distance between the pair of lines represented by the equation\[{{x}^{2}}-6xy+9{{y}^{2}}+\] \[3x-9y-4=0\]is:
A)
\[\frac{15}{\sqrt{10}}\]
done
clear
B)
\[\frac{1}{2}\]
done
clear
C)
\[\sqrt{\frac{5}{2}}\]
done
clear
D)
\[\frac{1}{\sqrt{10}}\]
done
clear
E)
\[\frac{1}{5}\]
done
clear
View Answer play_arrow
question_answer 222) If\[tan\text{ }A+cot\text{ }A=4,\]then\[ta{{n}^{4}}A+co{{t}^{4}}A\]is equal to:
A)
110
done
clear
B)
191
done
clear
C)
80
done
clear
D)
194
done
clear
E)
195
done
clear
View Answer play_arrow
question_answer 223) If\[\tan \left( \frac{\theta }{2} \right)=t,\]then\[\left( \frac{1-{{t}^{2}}}{1+{{t}^{2}}} \right)\]is equal to:
A)
\[\cos \theta \]
done
clear
B)
\[\sin \theta \]
done
clear
C)
\[\sec \theta \]
done
clear
D)
\[\cos \theta \]
done
clear
E)
\[\tan \theta \]
done
clear
View Answer play_arrow
question_answer 224) The period of the function\[y=sin\text{ }2x\]is:
A)
\[2\pi \]
done
clear
B)
\[\pi \]
done
clear
C)
\[\frac{\pi }{2}\]
done
clear
D)
\[4\pi \]
done
clear
E)
\[3\pi \]
done
clear
View Answer play_arrow
question_answer 225) If the angle of elevation of the top of a tower at a distance 500 m from its foot is 30°, then the height of the tower is:
A)
\[\frac{1}{\sqrt{3}}m\]
done
clear
B)
\[500\sqrt{3}m\]
done
clear
C)
\[\sqrt{3}m\]
done
clear
D)
\[\frac{1}{500}m\]
done
clear
E)
\[\frac{500}{\sqrt{3}}m\]
done
clear
View Answer play_arrow
question_answer 226) In triangle\[ABC,\text{ }a({{b}^{2}}+{{c}^{2}})cos\text{ }A+b({{c}^{2}}+{{a}^{2}})\] \[cos\text{ }B+c({{a}^{2}}+{{b}^{2}})cos\text{ }C\] is equal to:
A)
\[abc\]
done
clear
B)
\[2\,abc\]
done
clear
C)
\[3\,abc\]
done
clear
D)
\[4\,abc\]
done
clear
E)
0
done
clear
View Answer play_arrow
question_answer 227) The measures of the sides of a triangle are 3, 5 and 7. The greatest angle is:
A)
\[60{}^\circ \]
done
clear
B)
\[100{}^\circ \]
done
clear
C)
\[90{}^\circ \]
done
clear
D)
\[120{}^\circ \]
done
clear
E)
\[140{}^\circ \]
done
clear
View Answer play_arrow
question_answer 228) If in triangle\[ABC,\text{ }cos\text{ }A=cos\text{ }B\text{ }cos\text{ }C,\]then \[cot\text{ }B\text{ }cot\text{ }C\]is equal to:
A)
2
done
clear
B)
3
done
clear
C)
4
done
clear
D)
5
done
clear
E)
\[\frac{1}{2}\]
done
clear
View Answer play_arrow
question_answer 229) If\[{{\tan }^{-1}}x+{{\tan }^{-1}}y+{{\tan }^{-1}}z=\pi ,\]then\[x+y+z\]is:
A)
\[xyz\]
done
clear
B)
0
done
clear
C)
1
done
clear
D)
\[2xyz\]
done
clear
E)
\[{{x}^{2}}+{{y}^{2}}+{{z}^{2}}\]
done
clear
View Answer play_arrow
question_answer 230) If\[\theta ={{\sin }^{-1}}[\sin (-600{}^\circ )],\]then one of the possible values of\[\theta \]is:
A)
\[\frac{\pi }{3}\]
done
clear
B)
\[\frac{\pi }{2}\]
done
clear
C)
\[\frac{2\pi }{3}\]
done
clear
D)
\[-\frac{2\pi }{3}\]
done
clear
E)
0
done
clear
View Answer play_arrow
question_answer 231) If \[x\sin 45{}^\circ {{\cos }^{2}}60{}^\circ =\frac{{{\tan }^{2}}60{}^\circ \cos ec30{}^\circ }{\sec 45{}^\circ {{\cot }^{2}}30{}^\circ }\]then\[x\]is equal to:
A)
2
done
clear
B)
4
done
clear
C)
8
done
clear
D)
16
done
clear
E)
32
done
clear
View Answer play_arrow
question_answer 232) The centre of a circle is\[(2,-3)\]and the circumference is\[10\pi \]Then the equation of the circle is:
A)
\[{{x}^{2}}+{{y}^{2}}+4x+6y+12=0.\]
done
clear
B)
\[{{x}^{2}}+{{y}^{2}}-4x+6y+12=0\]
done
clear
C)
\[{{x}^{2}}+{{y}^{2}}-4x+6y-12=0\]
done
clear
D)
\[{{x}^{2}}+{{y}^{2}}-4x-6y-12=0\]
done
clear
E)
\[{{x}^{2}}+{{y}^{2}}-4x-6y+12=0\]
done
clear
View Answer play_arrow
question_answer 233) If the two circles\[2{{x}^{2}}+2{{y}^{2}}-3x+6y+k=0\]and\[{{x}^{2}}+{{y}^{2}}-4x+10y+16=0\]cut orthogonally, then the value of k is:
A)
41
done
clear
B)
14
done
clear
C)
4
done
clear
D)
0
done
clear
E)
2
done
clear
View Answer play_arrow
question_answer 234) The parabola\[{{y}^{2}}=x\]is symmetric about:
A)
\[x-\]axis
done
clear
B)
\[y-\]axis
done
clear
C)
both\[x\]and y axes
done
clear
D)
the line\[y=x\]
done
clear
E)
the line\[x=-y\]
done
clear
View Answer play_arrow
question_answer 235) The equation of the parabola whose vertex is at\[(2,-1)\]and focus at\[(2,-3),\]is:
A)
\[{{x}^{2}}-4x-8y-12=0\]
done
clear
B)
\[{{x}^{2}}-4x+8y+12=0\]
done
clear
C)
\[{{x}^{2}}+8y=12\]
done
clear
D)
\[{{x}^{2}}-4x+12=0\]
done
clear
E)
none of the above
done
clear
View Answer play_arrow
question_answer 236) The centroid of a triangle is (2, 7) and two of its vertices are (4, 8) and\[(-2,6)\]. The third vertex is:
A)
(0, 0)
done
clear
B)
(4, 7)
done
clear
C)
(7, 4)
done
clear
D)
(7, 7)
done
clear
E)
(4, 4)
done
clear
View Answer play_arrow
question_answer 237) The line\[y=mx+c\]touches the curve\[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1,\]if:
A)
\[{{c}^{2}}={{a}^{2}}{{m}^{2}}+{{b}^{2}}\]
done
clear
B)
\[{{c}^{2}}={{a}^{2}}{{m}^{2}}-{{b}^{2}}\]
done
clear
C)
\[{{c}^{2}}={{b}^{2}}{{m}^{2}}-{{a}^{2}}\]
done
clear
D)
\[{{a}^{2}}={{b}^{2}}{{m}^{2}}+{{c}^{2}}\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 238) The length of the tangent from a point on the circle \[{{x}^{2}}+{{y}^{2}}+2gx+2fy+{{c}_{1}}=0\]to the circle \[{{x}^{2}}+{{y}^{2}}+2gx+2fy+{{c}_{2}}=0\]is:
A)
\[\sqrt{{{c}_{2}}-{{c}_{1}}}\]
done
clear
B)
\[{{c}_{2}}-{{c}_{1}}\]
done
clear
C)
\[0\]
done
clear
D)
\[{{c}_{1}}-{{c}_{2}}\]
done
clear
E)
none of these
done
clear
View Answer play_arrow
question_answer 239) The eccentricity of the conic\[9{{x}^{2}}+25{{y}^{2}}=225\] is:
A)
\[\frac{2}{5}\]
done
clear
B)
\[\frac{4}{5}\]
done
clear
C)
\[\frac{1}{3}\]
done
clear
D)
\[\frac{1}{5}\]
done
clear
E)
\[\frac{3}{5}\]
done
clear
View Answer play_arrow
question_answer 240) The angles of a triangle are in the ratio\[1:3:5\]. Then the greatest angle is:
A)
\[\frac{5\pi }{9}\]
done
clear
B)
\[\frac{2\pi }{9}\]
done
clear
C)
\[\frac{7\pi }{9}\]
done
clear
D)
\[\frac{11\pi }{9}\]
done
clear
E)
\[\frac{\pi }{9}\]
done
clear
View Answer play_arrow
question_answer 241) A circular wire of radius 7 cm is cut and bend again into an arc of a circle of radius 12 cm. Then angle subtended by the arc at the centre is:
A)
\[50{}^\circ \]
done
clear
B)
\[210{}^\circ \]
done
clear
C)
\[100{}^\circ \]
done
clear
D)
\[60{}^\circ \]
done
clear
E)
\[30{}^\circ \]
done
clear
View Answer play_arrow