A) \[Mg(\sqrt{2}+1)\]
B) \[Mg\sqrt{2}\]
C) \[\frac{Mg}{\sqrt{2}}\]
D) \[Mg(\sqrt{2}-1)\]
Correct Answer: D
Solution :
Here, the constant horizontal force required to take the body from position 1 to position 2 can be calculated by using work-energy theorem. Let us assume that body is taken slowly so that its speed doesn't change, then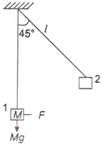 \[={{W}_{F}}+{{W}_{Mg}}+{{W}_{tension}}\] [symbols have their usual meanings] \[={{W}_{F}}=F\times l\,\sin \,{{45}^{o}},\] \[{{W}_{ & Mg}}={{M}_{g}}(l-l\,\cos \,{{45}^{o}}),\]\[{{W}_{tension}}=0\] \[\therefore \] \[F=Mg(\sqrt{2}-1)\]
\[={{W}_{F}}+{{W}_{Mg}}+{{W}_{tension}}\] [symbols have their usual meanings] \[={{W}_{F}}=F\times l\,\sin \,{{45}^{o}},\] \[{{W}_{ & Mg}}={{M}_{g}}(l-l\,\cos \,{{45}^{o}}),\]\[{{W}_{tension}}=0\] \[\therefore \] \[F=Mg(\sqrt{2}-1)\]
You need to login to perform this action.
You will be redirected in
3 sec
