A) \[(3,\,\,7)\]
B) \[(1,\,\,7)\]
C) \[(-3,\,\,7)\]
D) \[(-1,\,\,7)\]
Correct Answer: A
Solution :
Given, \[A=(3,3),E=(-3,6)\] and \[F=(9,6)\]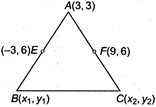 Let \[B=({{x}_{1}},{{y}_{1}})\] and \[C=({{x}_{2}},{{y}_{2}})\] Then, \[\frac{{{x}_{1}}+3}{2}=-3,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{{y}_{1}}+3}{2}=6\] \[\Rightarrow \] \[{{x}_{1}}=-9,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{y}_{1}}=9\] and \[\frac{{{x}_{2}}+3}{2}=9,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{{y}_{2}}+3}{2}=6\] \[\Rightarrow \] \[{{x}_{2}}=15,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{y}_{2}}=9\] Now, centroid \[=\left( \frac{-9+15+3}{3},\frac{9+9+3}{3} \right)\] \[=(3,7)\]
Let \[B=({{x}_{1}},{{y}_{1}})\] and \[C=({{x}_{2}},{{y}_{2}})\] Then, \[\frac{{{x}_{1}}+3}{2}=-3,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{{y}_{1}}+3}{2}=6\] \[\Rightarrow \] \[{{x}_{1}}=-9,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{y}_{1}}=9\] and \[\frac{{{x}_{2}}+3}{2}=9,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{{y}_{2}}+3}{2}=6\] \[\Rightarrow \] \[{{x}_{2}}=15,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{y}_{2}}=9\] Now, centroid \[=\left( \frac{-9+15+3}{3},\frac{9+9+3}{3} \right)\] \[=(3,7)\]
You need to login to perform this action.
You will be redirected in
3 sec
