A) \[1<e<\frac{2}{\sqrt{3}}\]
B) \[e=\frac{2}{\sqrt{3}}\]
C) \[e=\frac{\sqrt{3}}{2}\]
D) \[e>\frac{2}{\sqrt{3}}\]
Correct Answer: B
Solution :
Let the hyperbola be \[\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}=1\] and any double ordinate \[PO\] be\[(a\sec \theta ,\,\,b\tan \theta ),\,\,(a\sec \theta ,\,\,-b\tan \theta )\] and \[O\] is centre\[(0,\,\,0)\]. \[\Delta OPQ\]being equilateral.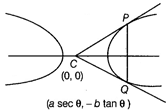 \[\Rightarrow \] \[\tan {{30}^{o}}=\frac{b\tan \theta }{a\sec \theta }\] \[\Rightarrow \] \[3\frac{{{b}^{2}}}{{{a}^{2}}}=\cos \text{e}{{\text{c}}^{2}}\theta \] \[\Rightarrow \] \[3({{e}^{2}}-1)=\cos \text{e}{{\text{c}}^{2}}\theta \] Now, \[\cos \text{e}{{\text{c}}^{2}}\theta \ge 1\] \[\Rightarrow \] \[3({{e}^{2}}-1)\ge 1\] \[\Rightarrow \] \[{{e}^{2}}\ge 4/3\] \[\Rightarrow \] \[e>\frac{2}{\sqrt{3}}\]
\[\Rightarrow \] \[\tan {{30}^{o}}=\frac{b\tan \theta }{a\sec \theta }\] \[\Rightarrow \] \[3\frac{{{b}^{2}}}{{{a}^{2}}}=\cos \text{e}{{\text{c}}^{2}}\theta \] \[\Rightarrow \] \[3({{e}^{2}}-1)=\cos \text{e}{{\text{c}}^{2}}\theta \] Now, \[\cos \text{e}{{\text{c}}^{2}}\theta \ge 1\] \[\Rightarrow \] \[3({{e}^{2}}-1)\ge 1\] \[\Rightarrow \] \[{{e}^{2}}\ge 4/3\] \[\Rightarrow \] \[e>\frac{2}{\sqrt{3}}\]
You need to login to perform this action.
You will be redirected in
3 sec
