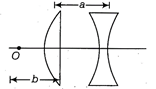
A) 20 cm
B) 60 cm
C) 40 cm
D) 30 cm
Correct Answer: C
Solution :
Focal length of the plano-convex lens is \[\frac{1}{f}=({{\mu }_{0}}-1)\left( \frac{1}{20}-\frac{1}{\infty } \right)\] \[=\left( \frac{3}{2}-1 \right)\left( \frac{1}{20} \right)=\frac{1}{2}\times \frac{1}{20}\] \[\Rightarrow \] \[t=40\,cm\] If point object O is placed at a distance of 40 cm from the plano-convex lens, rays become parallel and final image is formed at second focus or 40 cm from concave lens which is independent of a.You need to login to perform this action.
You will be redirected in
3 sec
