question_answer

The volume of the largest possible right circular cylinder that can be inscribed in a sphere of radius \[=\sqrt{3}\] is:

A) \[\frac{4}{3}\sqrt{3}\pi \]                            

B) \[\frac{8}{3}\sqrt{3}\pi \]

C) \[4\pi \]               

D) \[2\pi \]

Correct Answer: C

Solution :

Given, radius of sphere \[=\sqrt{3}\] Now, In \[\Delta OAB,\]by Pythagoras theorem \[{{(OA)}^{2}}={{(OB)}^{2}}+{{(AB)}^{2}}\]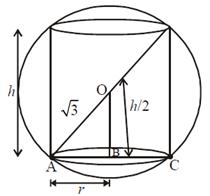 \[{{(\sqrt{3})}^{2}}={{\left( \frac{h}{2} \right)}^{2}}+{{r}^{2}}\] \[3={{\frac{h}{4}}^{2}}+{{r}^{2}}\Rightarrow \]                   ?(1) Now, volume of cylinder \[=\pi {{r}^{2}}h\] \[V=\pi \left( 3-\frac{{{h}^{2}}}{4} \right)h\]        (using eq. (1)) \[V=3\pi h-\frac{\pi {{h}^{2}}}{4}\]                                                           ?(2) Now, for largest possible right circular cylinder the volume must be maximum \[\therefore \]For maximum volume, \[\frac{dV}{dh}=0\] Now, Differentiating eq. (2) w.r.t. h \[{{V}^{1}}=\frac{dV}{dh}=3\pi -\frac{3}{4}\pi {{h}^{2}}\] or\[3\pi -\frac{3}{4}\pi {{h}^{2}}=0\Rightarrow \cancel{3\pi }=\frac{\cancel{3}}{4}\cancel{\pi }{{h}^{2}}\] \[\Rightarrow {{h}^{2}}=4\Rightarrow h=2\] Now, volume (V) of the cylinder \[=\pi \left( 3-\frac{{{h}^{2}}}{4} \right)h=\pi (6-2)=4\pi \]