A) \[\frac{{{v}^{2}}}{R}\hat{i}+\frac{{{v}^{2}}}{R}\hat{j}\]
B) \[-\frac{{{v}^{2}}}{R}\cos \theta \hat{i}+\frac{{{v}^{2}}}{R}\sin \theta \hat{j}\]
C) \[-\frac{{{v}^{2}}}{R}sin\theta \hat{i}+\frac{{{v}^{2}}}{R}\cos \theta \hat{j}\]
D) \[-\frac{{{v}^{2}}}{R}\cos \theta \hat{i}-\frac{{{v}^{2}}}{R}sin\theta \hat{j}\]
Correct Answer: D
Solution :
| [d] |
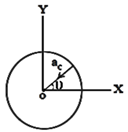 |
| \[\overrightarrow{a}={{a}_{c}}\cos \theta (-\hat{i})+{{a}_{c}}\sin \theta (-\hat{j})\] |
| \[\overrightarrow{a}=-\frac{{{V}^{2}}}{R}\cos \theta \hat{i}-\frac{{{V}^{2}}}{R}\sin \theta \hat{j}\] |
You need to login to perform this action.
You will be redirected in
3 sec
