question_answer

A heavy box is to dragged along a rough horizontal floor.

To do so, person A pushes it at an angle 30° from the horizontal and requires a minimum force \[{{F}_{A}},\] while person B pulls the box at an angle 60° from the horizontal and needs minimum force FB. If the coefficient of friction between the box and the floor is \[\frac{\sqrt{3}}{5},\]the ratio \[\frac{{{F}_{A}}}{{{F}_{B}}}\]is                [JEE ONLINE 19-04-2014]

A) \[\sqrt{3}\]

B) \[\frac{5}{\sqrt{3}}\]

C) \[\sqrt{\frac{3}{2}}\]

D) \[\frac{2}{\sqrt{3}}\]

Correct Answer: D

Solution :

[d]

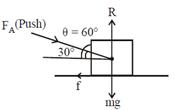\[{{F}_{A}}=\frac{\mu mg}{\sin \theta -\mu \cos \theta }\]Similarly,

\[{{F}_{B}}=\frac{\mu mg}{\sin \theta +\mu \cos \theta }\]

\[\therefore \] \[\frac{{{F}_{A}}}{{{F}_{B}}}=\frac{\frac{\mu mg}{\sin \theta -\mu \cos \theta }}{\frac{\mu mg}{\sin \theta +\mu \cos \theta }}\]

\[\frac{\frac{\mu mg}{\sin {{60}^{o}}-\frac{\sqrt{3}}{5}\cos {{60}^{o}}}}{\frac{\mu mg}{\sin {{30}^{o}}+\frac{\sqrt{3}}{5}\cos {{30}^{o}}}}\] \[\left[ \mu =\frac{\sqrt{3}}{5}\text{given} \right]\]

\[=\frac{\sin {{30}^{o}}+\frac{\sqrt{3}}{5}\cos {{30}^{o}}}{\sin {{60}^{o}}-\frac{\sqrt{3}}{5}\cos {{60}^{o}}}\]

\[=\frac{\frac{1}{2}+\frac{\sqrt{3}}{5}\times \frac{\sqrt{3}}{2}}{\frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{5}\times \frac{1}{2}}\] \[=\frac{\frac{1}{2}\left( 1+\frac{3}{5} \right)}{\frac{\sqrt{3}}{5}\left( 1-\frac{1}{5} \right)}=\frac{\frac{1}{2}\times \frac{8}{5}}{\frac{\sqrt{3}\times 4}{10}}\]

\[=\frac{\frac{8}{10}}{\frac{\sqrt{3}\times 4}{10}}=\frac{8}{\sqrt{3}\times 4}=\frac{2}{\sqrt{3}}\]