question_answer

The mass of a hydrogen molecule is \[3.32\times {{10}^{-27}}kg\].   If \[{{10}^{23}}\] hydrogen molecules strike, per second, a fixed wall of area \[\text{2 c}{{\text{m}}^{\text{2}}}\] at an angle of \[\text{45 }\!\!{}^\circ\!\!\text{ }\] to the normal, and rebound elastically with a speed of \[\text{1}{{\text{0}}^{\text{3}}}\text{ m/s}\], then the pressure on the wall is nearly: [JEE Main Online 08-04-2018]

A) \[\text{2}\text{.35}\times \text{1}{{\text{0}}^{2}}\,\,N/{{m}^{2}}\]

B) \[4.70\times {{10}^{2}}\,\,N/{{m}^{2}}\]

C) \[2.35\times {{10}^{3}}\,\,N/{{m}^{2}}\]

D) \[4.70\times {{10}^{3}}\,\,N/{{m}^{2}}\]

Correct Answer: C

Solution :

[c]

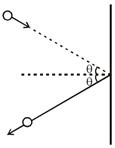Force = rate of change of momentum

(Perpendicular to area)

\[=n(2mu\,\,\cos \theta )\]

Pressure\[=\frac{Force}{Area}=\frac{n(2mu\,\,\cos \,\,\theta )}{A}\]

\[=\frac{3.32}{\sqrt{2}}\times \frac{{{10}^{-1}}}{{{10}^{-4}}}=\frac{3.32}{1.41}\times {{10}^{3}}=2.35\times {{10}^{3}}N/{{m}^{2}}\]