question_answer 1) In ruby laser, the stimulated emission is due to transition from
A)
metastable state to any lower state
done
clear
B)
any higher state to lower state
done
clear
C)
metastable state to ground state
done
clear
D)
any higher state to ground state
done
clear
View Answer play_arrow
question_answer 2) A direct current I flows along the length of an infinitely long straight thin walled pipe, then the magnetic field is
A)
uniform throughout the pipe but not zero
done
clear
B)
zero only along the axis of the pipe
done
clear
C)
zero at any point inside the pipe
done
clear
D)
maximum at the centre and minimum at the edge
done
clear
View Answer play_arrow
question_answer 3) A convex lens made of glass has focal length 0.15 m in air. If the refractive index of glass is\[\frac{3}{2}\] and that of water is \[\frac{4}{3}\] the focal length of lens when immersed in water is
A)
0.45m
done
clear
B)
0.15m
done
clear
C)
0.30m
done
clear
D)
0.6m
done
clear
View Answer play_arrow
question_answer 4) Two sources are said to be coherent if they produce waves
A)
having a constant phase difference
done
clear
B)
of equal wavelength
done
clear
C)
of equal speed
done
clear
D)
having same shape of wave from
done
clear
View Answer play_arrow
question_answer 5) Three resistors 1\[\Omega \], 2\[\Omega \] and 3\[\Omega \] are connected to form a triangle. Across 3\[\Omega \] resistor a 3 V battery is connected. The current through 3\[\Omega \] resistor is
A)
0.75 A
done
clear
B)
1 A
done
clear
C)
2 A
done
clear
D)
1.5 A
done
clear
View Answer play_arrow
question_answer 6) In a common emitter amplifier the input signal is applied across
A)
anywhere
done
clear
B)
emitter-collector
done
clear
C)
collector-base
done
clear
D)
base-emitter
done
clear
View Answer play_arrow
question_answer 7) In a radioactive disintegration, the ratio of initial number of atoms of the number of atoms present at an instant of time equal to its mean life is
A)
\[\frac{1}{{{e}^{2}}}\]
done
clear
B)
\[\frac{1}{e}\]
done
clear
C)
e
done
clear
D)
\[{{e}^{2}}\]
done
clear
View Answer play_arrow
question_answer 8) A ray of light is incident on a surface of glass slab at an angle 45\[^{0}C\] . If the lateral shift produced per unit thickness is \[\frac{1}{\sqrt{3}}\]m, the angle of refraction produced is
A)
\[{{\tan }^{-1}}\left( \frac{\sqrt{3}}{2} \right)\]
done
clear
B)
\[{{\tan }^{-1}}\left( 1-\frac{\sqrt{2}}{3} \right)\]
done
clear
C)
\[{{\sin }^{-1}}\left( 1-\frac{\sqrt{2}}{3} \right)\]
done
clear
D)
\[ta{{n}^{-1}}\left( \sqrt{\frac{2}{\sqrt{3}-1}} \right)\]
done
clear
View Answer play_arrow
question_answer 9) Ferromagnetic materials used in a transformer must have
A)
low permeability and high hysierisis loss
done
clear
B)
high permeability and low hysierisis loss
done
clear
C)
high permeability and high hystcrisis loss
done
clear
D)
low permeability and low hysterisis loss
done
clear
View Answer play_arrow
question_answer 10) According to Newtons corpuscular theory, the speed of light is
A)
same in all the media
done
clear
B)
lesser in rarer medium
done
clear
C)
lesser in denser medium
done
clear
D)
independent of [he medium
done
clear
View Answer play_arrow
question_answer 11) For the constructive interference the path difference between the two interfering waves must be equal to
A)
\[(2n+1)\lambda \]
done
clear
B)
\[2n\pi \]
done
clear
C)
\[n\pi \]
done
clear
D)
\[(2n+1)\frac{\lambda }{2}\]
done
clear
View Answer play_arrow
question_answer 12) The accurate measurement of emf can be obtained using
A)
multimeter
done
clear
B)
voltmeter
done
clear
C)
voltameter
done
clear
D)
potentiometer
done
clear
View Answer play_arrow
question_answer 13) The kinetic energy of an electron gets tripled, then the de-Broglie wavelength associated with it changes by a factor
A)
\[\frac{1}{3}\]
done
clear
B)
\[\sqrt{3}\]
done
clear
C)
\[\frac{1}{\sqrt{3}}\]
done
clear
D)
3
done
clear
View Answer play_arrow
question_answer 14) Which of the following is not a thermodynamic coordinate?
A)
Gas constant (R)
done
clear
B)
Pressure (p)
done
clear
C)
Volume (V)
done
clear
D)
Temperature (T)
done
clear
View Answer play_arrow
question_answer 15) Two solid pieces, one of steel and the other of aluminium when immersed completely in water have equal weights. When the solid pieces are weighed in air
A)
the weight of aluminium is half the weight of steel
done
clear
B)
steel piece will weigh more
done
clear
C)
they have the same weight
done
clear
D)
aluminium piece will weigh more
done
clear
View Answer play_arrow
question_answer 16) The amount of energy released when one microgram of matter is annihilated is
A)
\[25kWh\]
done
clear
B)
\[9\times {{10}^{10}}kWh\]
done
clear
C)
\[3\times {{10}^{10}}kWh\]
done
clear
D)
\[0.5\times {{10}^{5}}kWh\]
done
clear
View Answer play_arrow
question_answer 17) The number of significant Figures in the numbers \[4.8000\,\times {{10}^{4}}\] and 48000.50 are respectively
A)
5 and 6
done
clear
B)
5 and 7
done
clear
C)
2 and 7
done
clear
D)
2 and 6
done
clear
View Answer play_arrow
question_answer 18) \[\beta \]-decay means emission of electron from
A)
innermost electron orbit
done
clear
B)
a stable nucleus
done
clear
C)
outermost electron orbit
done
clear
D)
radioactive nucleus
done
clear
View Answer play_arrow
question_answer 19) An electric heater rated 220 V and 550 W is connected to AC mains. The current drawn by it is
A)
0.8 A
done
clear
B)
2.5 A
done
clear
C)
0.4 A
done
clear
D)
1.25 A
done
clear
View Answer play_arrow
question_answer 20) A body of mass m moving along a straight line covers half the distance with a speed of\[2m{{s}^{-1}}\]. The remaining half of the distance is covered in two equal time intervals with a speed of \[3m{{s}^{-1}}\] and \[5m{{s}^{-1}}\] respectively. The average speed of the particle for the entire journey is
A)
\[\frac{3}{8}m{{s}^{-1}}\]
done
clear
B)
\[\frac{8}{3}m{{s}^{-1}}\]
done
clear
C)
\[\frac{4}{3}m{{s}^{-1}}\]
done
clear
D)
\[\frac{16}{3}m{{s}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 21) The moment of inertia of a circular ring of radius r and mass M about diameter is
A)
\[\frac{2}{5}m{{r}^{2}}\]
done
clear
B)
\[\frac{M{{r}^{2}}}{4}\]
done
clear
C)
\[\frac{M{{r}^{2}}}{2}\]
done
clear
D)
\[\frac{M{{r}^{2}}}{12}\]
done
clear
View Answer play_arrow
question_answer 22) A body of mass 0.05 kg is observed to fall with an acceleration of 9.5 \[m{{s}^{-2}}\]. The opposing force of air on the body is \[(g=9.8\,\,m{{s}^{-2}})\]
A)
0.015 N
done
clear
B)
0.15 N
done
clear
C)
0.030 N
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 23) The colloidal solution in which both the dispersed phase and dispersion medium are liquids are called
A)
emulsions
done
clear
B)
gels
done
clear
C)
foams
done
clear
D)
liquid crystals
done
clear
View Answer play_arrow
question_answer 24) In fog, photographs of the objects taken with infrared radiations are more clear than those obtained during visible light because
A)
\[I-R\]radiation has lesser wavelength than visible radiation
done
clear
B)
scattering of \[I-R\]tight is more than visible light
done
clear
C)
the intensity of \[I-R\] light from the object is less
done
clear
D)
scattering of\[I-R\] light is less than visible light
done
clear
View Answer play_arrow
question_answer 25) Three concurrent co-planar forces 1 N, 2 N and 3 N acting along different directions on a body
A)
can keep the body in equilibrium if 2 N and 3 N act at right angle
done
clear
B)
can keep the body in equilibrium if 1 N and 2 N act at right angle
done
clear
C)
cannot keep the body in equilibrium
done
clear
D)
can keep the body in equilibrium in 1 N and 3 N act at an acute angle
done
clear
View Answer play_arrow
question_answer 26) Sound waves transfer
A)
only energy not momentum
done
clear
B)
energy
done
clear
C)
momentum
done
clear
D)
Both (a) and (b)
done
clear
View Answer play_arrow
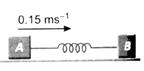
question_answer 27)
Two rectangular blocks A and B of masses 2 kg and 3 kg respectively are connected by a spring of spring constant 10.8 \[N{{m}^{-1}}\]and are placed on a frictionless horizontal surface. The block A was given an initial velocity of \[0.15\,m{{s}^{-1}}\] in the direction shown in the figure. The maximum compression of the spring during the motion is
A)
0.01 m
done
clear
B)
0.02m
done
clear
C)
0.05m
done
clear
D)
0.03m
done
clear
View Answer play_arrow
question_answer 28) G P Thomson experimentally confirmed the existence of matter waves by the phenomena
A)
diffraction
done
clear
B)
refraction
done
clear
C)
polarization
done
clear
D)
scattering
done
clear
View Answer play_arrow
question_answer 29) The resistance of a wire at 300 K is found to be 0.3\[\Omega \]. If the temperature coefficient of resistance of wire is\[1.5\times {{10}^{-3}}\,{{K}^{-1}}\,,\], the temperature at which the resistance becomes 0.6 \[\Omega \] is
A)
720 K
done
clear
B)
345 K
done
clear
C)
993 K
done
clear
D)
690 K
done
clear
View Answer play_arrow
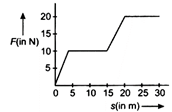
question_answer 30)
The work done by a force acting on a body is as shown in the graph. The total work done in covering an initial distance of 20 m is
A)
225 J
done
clear
B)
200 J
done
clear
C)
400 J
done
clear
D)
175 J
done
clear
View Answer play_arrow
question_answer 31) Two luminous point sources separated by a certain distance are at 10 km from an observer. If the aperture of his eye is \[2.5\times {{10}^{-3}}\]m and the wavelength of light used is 500 nm, the distance of separation between the point sources just seen to be resolved is
A)
12.2 m
done
clear
B)
24.2 m
done
clear
C)
2.44 m
done
clear
D)
1.22 m
done
clear
View Answer play_arrow
question_answer 32) A door 1.6 m wide requires a force of 1 N to be applied at the free end to open or close it. The force that is required at a point 0.4 m distance from the hinges for opening or closing the door is
A)
1.2 N
done
clear
B)
3.6 N
done
clear
C)
2.4 N
done
clear
D)
4 N
done
clear
View Answer play_arrow
question_answer 33) \[0.1\,{{m}^{3}}\] of water at \[80{}^\circ C\] is mixed with \[0.3\,{{m}^{3}}\] of water at \[60{}^\circ C\]. The final temperature of the mixture is
A)
\[65{}^\circ C\]
done
clear
B)
\[70{}^\circ C\]
done
clear
C)
\[60{}^\circ C\]
done
clear
D)
\[75{}^\circ C\]
done
clear
View Answer play_arrow
question_answer 34) The spectral series of the hydrogen atom that lies in the visible region of the electromagnetic spectrum
A)
Paschen
done
clear
B)
Balmer
done
clear
C)
Lyman
done
clear
D)
Brackett
done
clear
View Answer play_arrow
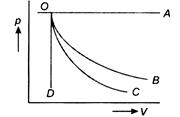
question_answer 35)
A graph of pressure versus volume for an ideal gas for different processes is as shown. In the graph curve OC represents
A)
isochoric process
done
clear
B)
isothermal process
done
clear
C)
isobaric process
done
clear
D)
adiabatic process
done
clear
View Answer play_arrow
question_answer 36) Which of the following statement does not hold good for thermal radiation?
A)
The wavelength changes when it travels from one medium to another
done
clear
B)
The frequency changes when it travels from one medium to another
done
clear
C)
The speed changes when it travels from one medium to another
done
clear
D)
They travel in straight line in a given medium
done
clear
View Answer play_arrow
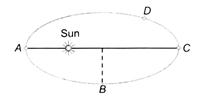
question_answer 37)
A planet revolves around the sun in an elliptical orbit. The linear speed of the planet will be maximum at
A)
D
done
clear
B)
B
done
clear
C)
A
done
clear
D)
C
done
clear
View Answer play_arrow
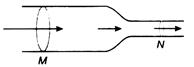
question_answer 38)
Horizontal tube of non-uniform cross-section has radii of 0.1 m and 0.05 m respectively at M and N. For a streamline flow of liquid the rate of liquid flow is
A)
changing continuously with time
done
clear
B)
greater at M than at N
done
clear
C)
greater at N than at M
done
clear
D)
same at M and N
done
clear
View Answer play_arrow
question_answer 39) A resistor and a capacitor are connected in series with an AC source. If the potential drop across the capacitor is 5 V and that across resistor is 12 V, then applied voltage is
A)
13V
done
clear
B)
17V
done
clear
C)
5V
done
clear
D)
12V
done
clear
View Answer play_arrow
question_answer 40) The amount of heat energy radiated by a metal at temperature T is E. When the temperature is increased to 3T, energy radiated is
A)
81E
done
clear
B)
9E
done
clear
C)
3E
done
clear
D)
27E
done
clear
View Answer play_arrow
question_answer 41) The angle of minimum deviation for an incident light ray on an equilateral prism is equal to its refracting angle. The refractive index of its material is
A)
\[\frac{1}{\sqrt{2}}\]
done
clear
B)
\[\sqrt{3}\]
done
clear
C)
\[\frac{\sqrt{3}}{2}\]
done
clear
D)
\[\frac{3}{2}\]
done
clear
View Answer play_arrow
question_answer 42)
In the following combinations of logic gates, the outputs of A, B and C are respectively
A)
0, 1, 1
done
clear
B)
0, 1, 0
done
clear
C)
1, 1, 0
done
clear
D)
1, 0, 1
done
clear
View Answer play_arrow
question_answer 43) A stationary point source of sound emits sound uniformly in all directions in a non-absorbing medium. Two points P and Q are at a distance of 4 m and 9 m respectively from the source. The ratio of amplitudes of the waves at P and Q is
A)
\[\frac{3}{2}\]
done
clear
B)
\[\frac{4}{9}\]
done
clear
C)
\[\frac{2}{3}\]
done
clear
D)
\[\frac{9}{4}\]
done
clear
View Answer play_arrow
question_answer 44) A galvanometer of resistance 240\[\Omega \] allows only 4% of the main current after connecting a shunt resistance. The value of the shunt resistance is
A)
10\[\Omega \]
done
clear
B)
200\[\Omega \]
done
clear
C)
80\[\Omega \]
done
clear
D)
50\[\Omega \]
done
clear
View Answer play_arrow
question_answer 45) The phenomena in which proton flips is
A)
nuclear magnetic resonance
done
clear
B)
lasers
done
clear
C)
radioactivity
done
clear
D)
nuclear fusion
done
clear
View Answer play_arrow
question_answer 46) \[y=3\sin \pi \left( \frac{t}{2}-\frac{x}{4} \right)\] represents an equation of a progressive wave, where r is in second and x is in metre. The distance travelled by the wave in 5 s is
A)
8 m
done
clear
B)
10 m
done
clear
C)
5 m
done
clear
D)
32 m
done
clear
View Answer play_arrow
question_answer 47) According to the quark model, it is possible to build all the hadrons using
A)
2 quarks and 3 antiquarks
done
clear
B)
3 quarks and 2 antiquarks
done
clear
C)
3 quarks and 3 antiquarks
done
clear
D)
2 quarks and 2 antiquarks
done
clear
View Answer play_arrow
question_answer 48) Ana-particle of mass \[6.4\times {{10}^{27}}\]kg and charge \[3.2\times {{10}^{-19}}\] C is situated in a uniform electric field of \[1.6\times {{10}^{5}}\,V{{m}^{-1}}\] The velocity of the particle at the end of \[2\times {{10}^{-2}}\] m path when it starts from rest is
A)
\[3\sqrt{3}\times {{10}^{5}}m{{s}^{-1}}\]
done
clear
B)
\[5\times {{10}^{5}}m{{s}^{-1}}\]
done
clear
C)
\[16\times {{10}^{5}}m{{s}^{-1}}\]
done
clear
D)
\[4\sqrt{2}\times {{10}^{5}}m{{s}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 49) A cylindrical tube open at both the ends has a fundamental frequency of 390 Hz in air. If \[\frac{1}{4}\]th of the tube is immersed vertically in water the fundamental frequency of air column is
A)
260 Hz
done
clear
B)
130 Hz
done
clear
C)
390 Hz
done
clear
D)
520 Hz
done
clear
View Answer play_arrow
question_answer 50) The surface temperature of the stars if determined using
A)
Plancks law
done
clear
B)
Wiens displacement law
done
clear
C)
Rayleigh-Jeans law
done
clear
D)
Kirchhoffs law
done
clear
View Answer play_arrow
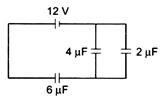
question_answer 51)
The charge deposited on 4uF capacitor in the circuit is
A)
\[6\times {{10}^{-6}}C\]
done
clear
B)
\[12\times {{10}^{-6}}C\]
done
clear
C)
\[24\times {{10}^{-6}}C\]
done
clear
D)
\[36\times {{10}^{-6}}C\]
done
clear
View Answer play_arrow
question_answer 52) A parallel beam of light is incident on a converging lens parallel to its principal axis. As one moves away from the lens on the other side of the principal axis, the intensity of light
A)
first decreases and then increases
done
clear
B)
continuously increases
done
clear
C)
continuously decreases
done
clear
D)
first increases and then decreases
done
clear
View Answer play_arrow
question_answer 53) Continuous emission spectrum is produced by
A)
incandescent electric lamp
done
clear
B)
mercury vapour lamp
done
clear
C)
sodium vapour lamp
done
clear
D)
polyatomic substances
done
clear
View Answer play_arrow
question_answer 54) A coil of n number of turns is wound tightly in the form of a spiral with inner and outer radii a and b respectively. When a current of strength\[I\] is passed through the coil, the magnetic field at its centre is
A)
\[\frac{{{\mu }_{0}}nI}{(b-a)}{{\log }_{e}}\frac{a}{b}\]
done
clear
B)
\[\frac{{{\mu }_{0}}nI}{2(b-a)}\]
done
clear
C)
\[\frac{2{{\mu }_{0}}nI}{b}\]
done
clear
D)
\[\frac{{{\mu }_{0}}nI}{2(b-a)}{{\log }_{e}}\frac{b}{a}\]
done
clear
View Answer play_arrow
question_answer 55) A ray of light is incident on a plane mirror at an angle of \[60{}^\circ \]. The angle of deviation produced by the minor is
A)
\[120{}^\circ \]
done
clear
B)
\[30{}^\circ \]
done
clear
C)
\[60{}^\circ \]
done
clear
D)
\[90{}^\circ \]
done
clear
View Answer play_arrow
question_answer 56) The electric potential at any point x, y, z in metres is given by\[V=3{{x}^{2}}.\]. The electric field at a point (2. 0, 1) is
A)
\[12\,V{{m}^{-1}}\]
done
clear
B)
\[-6\,V{{m}^{-1}}\]
done
clear
C)
\[6\,V{{m}^{-1}}\]
done
clear
D)
\[-12\,V{{m}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 57) Youngs double slit experiment gives interface fringes of width 0.3 mm. A thin glass plate made of material of refractive index 1.5 is kept in the path of light from one of the slits, then the fringe width becomes
A)
zero
done
clear
B)
0.3 mm
done
clear
C)
0.45 mm
done
clear
D)
0.15 mm
done
clear
View Answer play_arrow
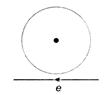
question_answer 58)
Near a circular loop of conducting wire as shown in the figure an electron moves along a straight line. The direction of the induced current if any in the loop is
A)
variable
done
clear
B)
clockwise
done
clear
C)
anticlockwise
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 59) Hydrogen atom from excited state comes to the ground stage by emitting a photon of wavelength \[\lambda \]. If R is the Rydberg constant, the principal quantum number n of the excited state
A)
\[\sqrt{\frac{\lambda R}{\lambda R-1}}\]
done
clear
B)
\[\sqrt{\frac{\lambda }{\lambda R-1}}\]
done
clear
C)
\[\sqrt{\frac{\lambda {{R}^{2}}}{\lambda R-1}}\]
done
clear
D)
\[\sqrt{\frac{\lambda R}{\lambda -1}}\]
done
clear
View Answer play_arrow
question_answer 60) The magnetic dipole moment of a current loop is independent of
A)
magnetic field in which it is lying
done
clear
B)
number of turns
done
clear
C)
area of the loop
done
clear
D)
current in the loop
done
clear
View Answer play_arrow
question_answer 61) The correct statement with regard to\[H_{2}^{+}\]and \[H_{2}^{-}\]is
A)
both\[H_{2}^{+}\]and\[H_{2}^{-}\]are equally stable
done
clear
B)
both\[H_{2}^{+}\]and\[H_{2}^{-}\]do not exist
done
clear
C)
\[H_{2}^{-}\] is more stable than\[H_{2}^{+}\]
done
clear
D)
\[H_{2}^{+}\]is more stable than\[H_{2}^{-}\]
done
clear
View Answer play_arrow
question_answer 62) Arrange the following in the increasing order of their bond order \[O2,\,\,O_{2}^{+},\,\,O_{2}^{-}\]and\[O_{2}^{2-}\]
A)
\[O_{2}^{2-},\,\,O_{2}^{-},\,\,{{O}_{2}},\,\,O_{2}^{+}\]
done
clear
B)
\[O_{2}^{2-},\,\,O_{2}^{-},\,\,O_{2}^{+},\,\,{{O}_{2}}\]
done
clear
C)
\[O_{2}^{+},\,\,{{O}_{2}},\,\,O_{2}^{-},\,\,O_{2}^{2-}\]
done
clear
D)
\[{{O}_{2}},\,\,O_{2}^{+},\,\,O_{2}^{-},\,\,O_{2}^{2-}\]
done
clear
View Answer play_arrow
question_answer 63) 2 g of\[a\cdot \]radioactive sample having half-life of 15 days was synthesized on 1st Jan 2009. The amount of the sample left behind on 1st March, 2009 (including both the days) is
A)
\[0\,\,g\]
done
clear
B)
\[0.125\,\,g\]
done
clear
C)
\[1\,\,g\]
done
clear
D)
\[0.5\,\,g\]
done
clear
View Answer play_arrow
question_answer 64) For a chemical reaction\[A\to B\], the rate of the reaction is\[2\times {{10}^{-3}}mol\,\,d{{m}^{-3}}{{s}^{-1}}\], when the initial concentration is\[0.05\,\,mol\,\,d{{m}^{-3}}\]. The rate of the same reaction is\[1.6\times {{10}^{-2}}mol\,\,d{{m}^{-3}}{{s}^{-1}}\]when the initial concentration is\[0.1\,\,mol\,\,d{{m}^{-3}}\]. The order of the reaction is
A)
2
done
clear
B)
0
done
clear
C)
3
done
clear
D)
1
done
clear
View Answer play_arrow
question_answer 65)
For the decomposition of a compound AB at 600 K, the following data were obtained
\[[AB]\,\,mol\,\,d{{m}^{-3}}\]
Rate of decomposition of\[AB\]in\[mol\,\,d{{m}^{-3}}\,\,{{s}^{-1}}\]
0.20
\[2.75\times {{10}^{-8}}\]
0.40
\[11.0\times {{10}^{-8}}\]
0.60
\[24.75\times {{10}^{-8}}\]
The order for the decomposition of AB is
A)
1.5
done
clear
B)
0
done
clear
C)
1
done
clear
D)
2
done
clear
View Answer play_arrow
question_answer 66) The rate equation for a reaction\[A\to B\]is\[r=k{{[A]}^{0}}\]. If the initial concentration of the reactant is a\[mol\,\,d{{m}^{-3}}\], the half-life period of the reaction is
A)
\[\frac{a}{2k}\]
done
clear
B)
\[\frac{k}{a}\]
done
clear
C)
\[\frac{a}{k}\]
done
clear
D)
\[\frac{2a}{k}\]
done
clear
View Answer play_arrow
question_answer 67) \[30\,\,cc\]of\[\frac{M}{3}HCl\],\[20\,\,cc\]of\[\frac{M}{2}HN{{O}_{3}}\]and\[40\,\,cc\] of\[\frac{M}{4}NaOH\]solutions are mixed and the volume was made up to \[\text{1}\,\,\text{d}{{\text{m}}^{3}}\]. The pH of the resulting solution is
A)
8
done
clear
B)
2
done
clear
C)
1
done
clear
D)
3
done
clear
View Answer play_arrow
question_answer 68) An aqueous solution containing\[\text{6}\text{.5}\,\,\text{g}\]of\[NaCl\]of\[90%\]purity was subjected to electrolysis. After the complete electrolysis, the solution was evaporated to get solid\[NaOH\]. The volume of\[1\,\,M\]acetic acid required to neutralize\[NaOH\]obtained above is
A)
\[1000\,\,c{{m}^{3}}\]
done
clear
B)
\[2000\,\,c{{m}^{3}}\]
done
clear
C)
\[100\,\,c{{m}^{3}}\]
done
clear
D)
\[200\,\,c{{m}^{3}}\]
done
clear
View Answer play_arrow
question_answer 69) The standard electrode potential for the half-cell reactions are \[Z{{n}^{2+}}+2{{e}^{-}}\xrightarrow{{}}Zn;\,\,{{E}^{o}}=-0.76\,\,V\] \[F{{e}^{2+}}+2{{e}^{-}}\xrightarrow{{}}Fe;\,\,{{E}^{o}}=-0.44\,\,V\] The emf of the cell reaction, \[F{{e}^{2+}}+Zn\xrightarrow{{}}Z{{n}^{2+}}+Fe\]is
A)
\[-0.32\,\,V\]
done
clear
B)
\[-1.20\,\,V\]
done
clear
C)
\[+1.20\,\,V\]
done
clear
D)
\[+0.32\,\,V\]
done
clear
View Answer play_arrow
question_answer 70) \[{{10}^{-6}}M\,\,NaOH\]is diluted 100 times. The\[pH\]of the diluted base is
A)
between 7 and 8
done
clear
B)
between 5 and 6
done
clear
C)
between 6 and 7
done
clear
D)
between 10 and 11
done
clear
View Answer play_arrow
question_answer 71) In the electrolysis of acidulated water, it is desired to obtain\[1.12\,\,cc\]of hydrogen per second under STP condition. The current to be passed is
A)
\[1.93\,\,A\]
done
clear
B)
\[9.65\,\,A\]
done
clear
C)
\[19.3\,\,A\]
done
clear
D)
\[0.965\,\,A\]
done
clear
View Answer play_arrow
question_answer 72) The one which decreases with dilution is
A)
molar conductance
done
clear
B)
conductance
done
clear
C)
specific conductance
done
clear
D)
equivalent conductance
done
clear
View Answer play_arrow
question_answer 73) Vapour pressure of pure A is 70 mm of\[Hg\]at\[{{25}^{o}}C\]. It forms an ideal solution with B in which mole fraction of A is 0.8. If the vapour pressure of the solution is 84 mm of Hg at\[{{25}^{o}}C\], the vapour pressure of pure B at\[{{25}^{o}}C\]is
A)
28mm
done
clear
B)
56mm
done
clear
C)
70mm
done
clear
D)
140mm
done
clear
View Answer play_arrow
question_answer 74) A 6% solution of urea is isotonic with
A)
1 M solution of glucose
done
clear
B)
0.05 M solution of glucose
done
clear
C)
6% solution of glucose
done
clear
D)
25% solution of glucose
done
clear
View Answer play_arrow
question_answer 75) In countries nearer to polar region, the roads are sprinkled with\[CaC{{l}_{2}}\]. This is
A)
to minimise the wear and tear of the roads
done
clear
B)
to minimise the snow fall
done
clear
C)
to minimise pollution
done
clear
D)
to minimise the accumulation of dust on the road
done
clear
View Answer play_arrow
question_answer 76) For the reaction\[{{H}_{2}}O(l){{H}_{2}}O(g)\]at\[373\,\,K\]and 1 aim pressure
A)
\[\Delta H=0\]
done
clear
B)
\[\Delta E=0\]
done
clear
C)
\[\Delta H=T\Delta S\]
done
clear
D)
\[\Delta H=\Delta E\]
done
clear
View Answer play_arrow
question_answer 77) A compound of\[A\]and\[B\]crystallizes in a cubic lattice in which A atoms occupy the lattice points at the corners of the cube. The\[B\]atoms occupy the centre of each face of the cube. The probable empirical formula of the compound is
A)
\[A{{B}_{2}}\]
done
clear
B)
\[{{A}_{3}}B\]
done
clear
C)
\[AB\]
done
clear
D)
\[A{{B}_{3}}\]
done
clear
View Answer play_arrow
question_answer 78) In electrophilic aromatic substitution reaction, the nitro group is meta directing because it
A)
decreases electron density at ortho and para positions
done
clear
B)
decreases electron density at meta position
done
clear
C)
increases electron density at meta position
done
clear
D)
increases electron density at ortho and para positions
done
clear
View Answer play_arrow
question_answer 79) \[C{{H}_{3}}COOH\xrightarrow{LiAl{{H}_{4}}}X\xrightarrow[{{300}^{o}}C]{Cu}Y\xrightarrow[NaOH]{Dilute}\] In the above reaction\[Z\]is
A)
butanol
done
clear
B)
aldol
done
clear
C)
ketol
done
clear
D)
acetal
done
clear
View Answer play_arrow
question_answer 80) The best method for the conversion of an alcohol into an alkyl chloride is by treating the alcohol with
A)
\[PC{{l}_{3}}\]
done
clear
B)
\[PC{{l}_{5}}\]
done
clear
C)
\[SOC{{l}_{2}}\]in presence of pyridine
done
clear
D)
dry\[HCl\]in the presence of anhydrous\[ZnC{{l}_{2}}\]
done
clear
View Answer play_arrow
question_answer 81) The electrophile involved in the sulphonation of benzene is
A)
\[SO_{3}^{+}\]
done
clear
B)
\[SO_{3}^{2-}\]
done
clear
C)
\[H_{3}^{+}O\]
done
clear
D)
\[S{{O}_{3}}\]
done
clear
View Answer play_arrow
question_answer 82) The carbon-carbon bond length in benzene is
A)
in between\[{{C}_{2}}{{H}_{6}}\]and\[{{C}_{2}}{{H}_{4}}\]
done
clear
B)
same as in\[{{C}_{2}}{{H}_{4}}\]
done
clear
C)
in between\[{{C}_{2}}{{H}_{6}}\]and\[{{C}_{2}}{{H}_{2}}\]
done
clear
D)
in between\[{{C}_{2}}{{H}_{4}}\]and\[{{C}_{2}}{{H}_{2}}\]
done
clear
View Answer play_arrow
question_answer 83) The compound which is not formed during the dry distillation of a mixture of calcium formate and calcium acetate is
A)
methanal
done
clear
B)
propanal
done
clear
C)
propanone
done
clear
D)
ethanol
done
clear
View Answer play_arrow
question_answer 84) An organic compound\[X\]is oxidized by using acidified\[{{K}_{2}}C{{r}_{2}}{{O}_{7}}\]. The product obtained reacts with phenyl hydrazine but does not answer silver mirror test. The possible structure of\[X\]is
A)
\[C{{H}_{3}}C{{H}_{2}}OH\]
done
clear
B)
\[C{{H}_{3}}-\underset{\begin{smallmatrix} || \\ O \end{smallmatrix}}{\mathop{C}}\,-C{{H}_{3}}\]
done
clear
C)
\[{{(C{{H}_{3}})}_{2}}CHOH\]
done
clear
D)
\[C{{H}_{3}}CHO\]
done
clear
View Answer play_arrow
question_answer 85) The reaction involved in the oil of winter green test is salicylic acid\[\xrightarrow[Conc.{{H}_{2}}S{{O}_{4}}]{\Delta }\]product. The product is treated with\[N{{a}_{2}}C{{O}_{3}}\]solution. The missing reagent in the above reaction is
A)
phenol
done
clear
B)
\[NaOH\]
done
clear
C)
ethanol
done
clear
D)
methanol
done
clear
View Answer play_arrow
question_answer 86) The compound which forms acetaldehyde when heated with dilute\[NaOH\], is
A)
1, 1-dichloroethane
done
clear
B)
1, 1, 1-trichloroethane
done
clear
C)
1-chloroethane
done
clear
D)
1, 2-dichloroethane
done
clear
View Answer play_arrow
question_answer 87) Arrange the following in the increasing order of their basic strengths\[C{{H}_{3}}N{{H}_{2}},\]\[{{(C{{H}_{3}})}_{2}}NH\]\[{{(C{{H}_{3}})}_{3}}N,\,\,N{{H}_{3}}\]
A)
\[N{{H}_{3}}<{{(C{{H}_{3}})}_{3}}N<{{(C{{H}_{3}})}_{2}}NH<C{{H}_{3}}N{{H}_{2}}\]
done
clear
B)
\[N{{H}_{3}}<{{(C{{H}_{3}})}_{3}}N<C{{H}_{3}}N{{H}_{2}}<{{(C{{H}_{3}})}_{2}}NH\]
done
clear
C)
\[{{(C{{H}_{3}})}_{3}}N<N{{H}_{3}}<C{{H}_{3}}N{{H}_{2}}<{{(C{{H}_{3}})}_{2}}NH\]
done
clear
D)
\[C{{H}_{3}}N{{H}_{2}}<{{(C{{H}_{3}})}_{2}}NH<{{(C{{H}_{3}})}_{3}}N<N{{H}_{3}}\]
done
clear
View Answer play_arrow
question_answer 88) The one which has least iodine value is
A)
sunflower oil
done
clear
B)
ginger oil
done
clear
C)
ghee
done
clear
D)
groundnut oil
done
clear
View Answer play_arrow
question_answer 89) A diabetic person carries a packet of glucose with him always, because
A)
glucose reduces the blood sugar level slowly
done
clear
B)
glucose increases the blood sugar level slowly
done
clear
C)
glucose reduces the blood sugar level
done
clear
D)
glucose increases the blood sugar level almost instantaneously
done
clear
View Answer play_arrow
question_answer 90) There are 20 naturally occurring amino acids. The maximum number of tripeptides that can be obtained is
A)
8000
done
clear
B)
6470
done
clear
C)
7465
done
clear
D)
5360
done
clear
View Answer play_arrow
question_answer 91) Cooking is fast in a pressure cooker, because
A)
food particles are effectively smashed
done
clear
B)
water boils at higher temperature inside the pressure cooker
done
clear
C)
food is cooked at constant volume
done
clear
D)
loss of heat due to radiation is minimum
done
clear
View Answer play_arrow
question_answer 92) The ore that is concentrated by froth floatation process is
A)
zincite
done
clear
B)
cinnabar
done
clear
C)
bauxite
done
clear
D)
malachite
done
clear
View Answer play_arrow
question_answer 93) The correct set of four quantum numbers for outermost electron of potassium\[(Z=19)\]is
A)
\[4,\,\,1,\,\,0,\,\,\frac{1}{2}\]
done
clear
B)
\[3,\,\,1,\,\,0,\,\,\frac{1}{2}\]
done
clear
C)
\[4,\,\,0,\,\,0,\,\,\frac{1}{2}\]
done
clear
D)
\[3,\,\,0,\,\,0,\,\,\frac{1}{2}\]
done
clear
View Answer play_arrow
question_answer 94) A body of mass\[x\]kg is moving with a velocity of\[100\,\,m{{s}^{-1}}\]. Its de-Broglie wavelength is\[6.62\times {{10}^{-35}}m\]. Hence,\[x\]is\[(h=6.62\times {{10}^{-34}}Js)\]
A)
0.1 kg
done
clear
B)
0.25 kg
done
clear
C)
0.15kg
done
clear
D)
0.2kg
done
clear
View Answer play_arrow
question_answer 95) The correct order of ionization energy of C, N, O, F is
A)
F < O < N < C
done
clear
B)
F < N < C < O
done
clear
C)
C < N < O < F
done
clear
D)
C < O < N < F
done
clear
View Answer play_arrow
question_answer 96) The oxide of an element whose electronic configuration is\[1{{s}^{2}},\,\,2{{s}^{2}},\,\,2{{p}^{6}},\,\,3{{s}^{1}}\]is
A)
neutral
done
clear
B)
amphoteric
done
clear
C)
basic
done
clear
D)
acidic
done
clear
View Answer play_arrow
question_answer 97) The characteristic not related to alkali metal is
A)
high ionization energy
done
clear
B)
their ions are isoelectronic with noble gases
done
clear
C)
low melting point
done
clear
D)
low electronegativity
done
clear
View Answer play_arrow
question_answer 98) Among the following, the compound that contains ionic, covalent and coordinate linkage is
A)
\[N{{H}_{3}}\]
done
clear
B)
\[N{{H}_{4}}Cl\]
done
clear
C)
\[NaCl\]
done
clear
D)
\[CaO\]
done
clear
View Answer play_arrow
question_answer 99) A covalent molecule\[A{{B}_{3}}\]has pyramidal structure. The number of lone pair and bond pair of electrons in the molecule are respectively
A)
2 and 2
done
clear
B)
0 and 4
done
clear
C)
3 and 1
done
clear
D)
1 and 3
done
clear
View Answer play_arrow
question_answer 100) Excess of carbon dioxide is passed through\[50\,\,mL\]of\[0.5\,\,M\]calcium hydroxide solution. After the completion of the reaction, the solution was evaporated to dryness. The solid calcium carbonate was completely neutralized with\[0.1\,\,N\]hydrochloric acid. The volume of hydrochloric acid required is (Atomic mass of calcium = 40)
A)
\[300\,\,c{{m}^{3}}\]
done
clear
B)
\[200\,\,c{{m}^{3}}\]
done
clear
C)
\[500\,\,c{{m}^{3}}\]
done
clear
D)
\[400\,\,c{{m}^{3}}\]
done
clear
View Answer play_arrow
question_answer 101) A bivalent metal has an equivalent mass of 32. The molecular mass of the metal nitrate is
A)
182
done
clear
B)
168
done
clear
C)
192
done
clear
D)
188
done
clear
View Answer play_arrow
question_answer 102) The rms velocity of molecules of a gas of density\[4\,\,kg\,\,{{m}^{-3}}\]and pressure\[1.2\times {{10}^{5}}\,\,N{{m}^{-2}}\]is
A)
\[300\,\,m{{s}^{-1}}\]
done
clear
B)
\[900\,\,m{{s}^{-1}}\]
done
clear
C)
\[120\,\,m{{s}^{-1}}\]
done
clear
D)
\[600\,\,m{{s}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 103) 0.5 mole of each of\[{{H}_{2}},\,\,S{{O}_{2}}\]and\[C{{H}_{4}}\]are kept in a container. A hole was made in the container. After 3 h, the order of partial pressures in the container will be
A)
\[pS{{O}_{2}}>p{{H}_{2}}>pC{{H}_{4}}\]
done
clear
B)
\[pS{{O}_{2}}>pC{{H}_{4}}>p{{H}_{2}}\]
done
clear
C)
\[p{{H}_{2}}>pS{{O}_{2}}>pC{{H}_{4}}\]
done
clear
D)
\[p{{H}_{2}}>pC{{H}_{4}}>pS{{O}_{2}}\]
done
clear
View Answer play_arrow
question_answer 104) The enthalpy of formation of\[N{{H}_{3}}\]is\[-46\,\,kJ\,\,mo{{l}^{-1}}\]. The enthalpy change for the reaction \[2N{{H}_{3}}(g)\xrightarrow{{}}{{N}_{2}}(g)+3{{H}_{2}}(g)\]is
A)
\[+184\,\,kJ\]
done
clear
B)
\[+23\,\,kJ\]
done
clear
C)
\[+92\,\,kJ\]
done
clear
D)
\[+46\,\,kJ\]
done
clear
View Answer play_arrow
question_answer 105) 5 moles of\[S{{O}_{2}}\]and 5 moles of\[{{O}_{2}}\]are allowed to react. At equilibrium, it was found that 60% of\[S{{O}_{2}}\]is used up. If the partial pressure of the equilibrium mixture is one atmosphere, the partial pressure of\[{{O}_{2}}\]is
A)
\[0.82\,\,atm\]
done
clear
B)
\[0.52\,\,atm\]
done
clear
C)
\[0.21\,\,atm\]
done
clear
D)
\[0.41\,\,atm\]
done
clear
View Answer play_arrow
question_answer 106) \[2HI(g){{H}_{2}}(g)+{{I}_{2}}(g)\] The equilibrium constant of the above reaction is\[6.4\]at\[300\,\,K\]. If 0.25 mole each of\[{{H}_{2}}\]and \[{{I}_{2}}\] are added to the system, the equilibrium constant will be
A)
6.4
done
clear
B)
0.8
done
clear
C)
3.2
done
clear
D)
1.6
done
clear
View Answer play_arrow
question_answer 107) Rate of physical adsorption increases with
A)
decrease in surface area
done
clear
B)
decrease in temperature
done
clear
C)
decrease in pressure
done
clear
D)
increase in temperature
done
clear
View Answer play_arrow
question_answer 108) \[IUPAC\]name of\[{{(C{{H}_{3}})}_{3}}CCl\]is
A)
\[n-\]butyl chloride
done
clear
B)
3-chloro butane
done
clear
C)
2-chloro 2-methyl propane
done
clear
D)
\[t-\]butyl chloride
done
clear
View Answer play_arrow
question_answer 109) Lucas test is associated with
A)
aldehydes
done
clear
B)
phenols
done
clear
C)
carboxylic acids
done
clear
D)
alcohols
done
clear
View Answer play_arrow
question_answer 110) An organic compound on heating with\[CuO\]produces\[C{{O}_{2}}\]but no water. The organic compound may be
A)
carbon tetrachloride
done
clear
B)
chloroform
done
clear
C)
methane
done
clear
D)
ethyl iodide
done
clear
View Answer play_arrow
question_answer 111) The condensation polymer among the following is
A)
rubber
done
clear
B)
protein
done
clear
C)
PVC
done
clear
D)
polyethene
done
clear
View Answer play_arrow
question_answer 112) The order of stability of metal oxides is
A)
\[A{{l}_{2}}{{O}_{3}}<MgO<F{{e}_{2}}{{O}_{3}}<C{{r}_{2}}{{O}_{3}}\]
done
clear
B)
\[C{{r}_{2}}{{O}_{3}}<MgO<A{{l}_{2}}{{O}_{3}}<F{{e}_{2}}{{O}_{3}}\]
done
clear
C)
\[F{{e}_{2}}{{O}_{3}}<C{{r}_{2}}{{O}_{3}}<A{{l}_{2}}{{O}_{3}}<MgO\]
done
clear
D)
\[F{{e}_{2}}{{O}_{3}}<A{{l}_{2}}{{O}_{3}}<C{{r}_{2}}{{O}_{3}}<MgO\]
done
clear
View Answer play_arrow
question_answer 113) The temperature of the slag zone in the metallurgy of iron using blast furnace is
A)
\[1200-{{1500}^{o}}C\]
done
clear
B)
\[1500-{{1600}^{o}}C\]
done
clear
C)
\[400-{{700}^{o}}C\]
done
clear
D)
\[800-{{1000}^{o}}C\]
done
clear
View Answer play_arrow
question_answer 114) The function of\[Fe{{(OH)}_{3}}\]in the contact process is
A)
to remove arsenic impurity
done
clear
B)
to detect colloidal impurity
done
clear
C)
to remove moisture
done
clear
D)
to remove dust particles
done
clear
View Answer play_arrow
question_answer 115) In which of the following, \[N{{H}_{3}}\] is not used?
A)
Tollens reagent
done
clear
B)
Nesslers reagent
done
clear
C)
Group reagent for the analysis of IV group basic radicals
done
clear
D)
Group reagent for the analysis of III group basic radicals
done
clear
View Answer play_arrow
question_answer 116) Argon is used
A)
in filling airships
done
clear
B)
to obtain low temperature
done
clear
C)
in high temperature welding
done
clear
D)
in radiotherapy for treatment of cancer
done
clear
View Answer play_arrow
question_answer 117) The incorrect statement in respect of chromyl chloride test is
A)
formation of red vapours
done
clear
B)
formation of lead chromate
done
clear
C)
formation of chromyl chloride
done
clear
D)
liberation of chlorine
done
clear
View Answer play_arrow
question_answer 118) The magnetic moment of a transition metal ion is\[\sqrt{15}\,\,BM\]. Therefore, the number of unpaired electrons present in it, is
A)
3
done
clear
B)
4
done
clear
C)
1
done
clear
D)
2
done
clear
View Answer play_arrow
question_answer 119) The\[IUPAC\]name of\[{{[Co{{(N{{H}_{3}})}_{5}}ONO]}^{2+}}\]ion is
A)
penta ammine nitrito cobalt (IV) ion
done
clear
B)
penta ammine nitrito cobalt (III) ion
done
clear
C)
penta ammine nitro cobalt (III) ion
done
clear
D)
penta ammine nitro cobalt (IV) ion
done
clear
View Answer play_arrow
question_answer 120) The oxidation state of Fe in the brown ring complex:\[[Fe{{({{H}_{2}}O)}_{5}}NO]S{{O}_{4}}\]is
A)
+3
done
clear
B)
0
done
clear
C)
+2
done
clear
D)
+1
done
clear
View Answer play_arrow
question_answer 121) If\[f:[2,\,\,3]\to R\] is defined by\[f(x)={{x}^{3}}+3x-2\], then the range\[f(x)\]is contained in the interval
A)
\[[1,\,\,12]\]
done
clear
B)
\[[12,\,\,34]\]
done
clear
C)
\[[35,\,\,50]\]
done
clear
D)
\[[-12,\,\,12]\]
done
clear
View Answer play_arrow
question_answer 122) \[\left\{ x\in R:\frac{2x-1}{{{x}^{3}}+4{{x}^{2}}+3x}\in R \right\}\]equals
A)
\[R-\{0\}\]
done
clear
B)
\[R-\{0,\,\,1,\,\,3\}\]
done
clear
C)
\[R-\{0,\,\,-1,\,\,-3\}\]
done
clear
D)
\[R-\left\{ 0,\,\,-1,\,\,-3,\,\,+\frac{1}{2} \right\}\]
done
clear
View Answer play_arrow
question_answer 123) Using mathematical induction, the numbers \[{{a}_{n}}s\]are defined by, \[{{a}_{0}}=1,\,\,{{a}_{n+1}}=3{{n}^{2}}+n+{{a}_{n}},(n\ge 0)\] Then, \[{{a}_{n}}\]is equal to
A)
\[{{n}^{3}}+{{n}^{2}}+1\]
done
clear
B)
\[{{n}^{3}}-{{n}^{2}}+1\]
done
clear
C)
\[{{n}^{3}}-{{n}^{2}}\]
done
clear
D)
\[{{n}^{3}}+{{n}^{2}}\]
done
clear
View Answer play_arrow
question_answer 124) The number of subsets of\[\{1,\,\,2,\,\,3,...,9\}\] containing at least one odd number is
A)
324
done
clear
B)
396
done
clear
C)
496
done
clear
D)
512
done
clear
View Answer play_arrow
question_answer 125) \[p\]points are chosen on each of the three coplanar lines. The maximum number of triangles formed with vertices at these points is
A)
\[{{p}^{3}}+3{{p}^{2}}\]
done
clear
B)
\[\frac{1}{2}({{p}^{3}}+p)\]
done
clear
C)
\[\frac{{{p}^{2}}}{2}(5p-3)\]
done
clear
D)
\[{{p}^{2}}(4p-3)\]
done
clear
View Answer play_arrow
question_answer 126) A binary sequence is an array of 0s and 1s. The number of n-digit binary sequences which contain even number of 0s is
A)
\[{{2}^{n-1}}\]
done
clear
B)
\[{{2}^{n}}-1\]
done
clear
C)
\[{{2}^{n-1}}-1\]
done
clear
D)
\[{{2}^{n}}\]
done
clear
View Answer play_arrow
question_answer 127) The coefficient of\[{{x}^{24}}\]in the expansion of\[{{(1+{{x}^{2}})}^{12}}(1+{{x}^{12}})(1+{{x}^{24}})\]
A)
\[^{12}{{C}_{6}}\]
done
clear
B)
\[^{12}{{C}_{6}}+2\]
done
clear
C)
\[^{12}{{C}_{6}}+4\]
done
clear
D)
\[^{12}{{C}_{6}}+6\]
done
clear
View Answer play_arrow
question_answer 128) If\[x\]is numerically so small so that\[{{x}^{2}}\]and higher powers of\[x\]can be neglected, then\[{{\left( 1+\frac{2x}{3} \right)}^{3/2}}\cdot {{(32+5x)}^{-1/5}}\]is approximately equal to
A)
\[\frac{32+31x}{64}\]
done
clear
B)
\[\frac{31+32x}{64}\]
done
clear
C)
\[\frac{31-32x}{64}\]
done
clear
D)
\[\frac{1-2x}{64}\]
done
clear
View Answer play_arrow
question_answer 129) For\[|x|\,\,<1\], the constant term in the expansion of\[\frac{1}{{{(x-1)}^{2}}(x-2)}\]is
A)
2
done
clear
B)
1
done
clear
C)
0
done
clear
D)
\[-\frac{1}{2}\]
done
clear
View Answer play_arrow
question_answer 130) \[\frac{1}{{{e}^{3x}}}({{e}^{x}}+{{e}^{5x}})={{a}_{0}}+{{a}_{1}}x+{{a}_{2}}{{x}^{2}}+...\]\[\Rightarrow \,\,\,2{{a}_{1}}+{{2}^{3}}{{a}_{3}}+{{2}^{5}}{{a}_{5}}+...\]is equal to
A)
\[e\]
done
clear
B)
\[{{e}^{-1}}\]
done
clear
C)
1
done
clear
D)
0
done
clear
View Answer play_arrow
question_answer 131) The roots of \[(x-a)(x-a-1)+(x-a-1)(x-a-2)\]\[+(x-a)(x-a-2)=0\], \[a\in R\]are always
A)
equal
done
clear
B)
imaginary
done
clear
C)
real and distinct
done
clear
D)
rational and equal
done
clear
View Answer play_arrow
question_answer 132) Let\[f(x)={{x}^{2}}+ax+b\], where\[a,\,\,b\in R\]. If\[f(x)=0\]has all its roots imaginary, then the roots of\[f(x)+f(x)+f(x)=0\]are
A)
real and distinct
done
clear
B)
imaginary
done
clear
C)
equal
done
clear
D)
rational and equal
done
clear
View Answer play_arrow
question_answer 133) If\[\alpha ,\,\,\beta ,\,\,\gamma \]are the roots of\[{{x}^{3}}+4x+1=0\], then the equation whose roots are\[\frac{{{\alpha }^{2}}}{\beta +\gamma },\,\,\frac{{{\beta }^{2}}}{\gamma +\alpha }\],\[\frac{{{\gamma }^{2}}}{\alpha +\beta }\] is
A)
\[{{x}^{3}}-4x-1=0\]
done
clear
B)
\[{{x}^{3}}-4x+1=0\]
done
clear
C)
\[{{x}^{3}}+4x-1=0\]
done
clear
D)
\[{{x}^{3}}+4x+1=0\]
done
clear
View Answer play_arrow
question_answer 134) If\[f(x)=2{{x}^{4}}-13{{x}^{2}}+ax+b\]is divisible by\[{{x}^{2}}-3x+2\], then\[(a,\,\,b)\]is equal to
A)
(-9,-2)
done
clear
B)
(6, 4)
done
clear
C)
(9, 2)
done
clear
D)
(2, 9)
done
clear
View Answer play_arrow
question_answer 135) Let\[A\]and\[B\]be two symmetric matrices of same order. Then, the matrix\[AB-BA\]is
A)
a symmetric matrix
done
clear
B)
a skew-symmetric matrix
done
clear
C)
a null matrix
done
clear
D)
the identity matrix
done
clear
View Answer play_arrow
question_answer 136) If one of the roots of\[\left| \begin{matrix} 3 & 5 & x \\ 7 & x & 7 \\ x & 5 & 3 \\ \end{matrix} \right|=0\]is\[-10\], then the other roots are
A)
3, 7
done
clear
B)
4, 7
done
clear
C)
3, 9
done
clear
D)
3, 4
done
clear
View Answer play_arrow
question_answer 137) If\[x,\,\,y,\,\,z\]are all positive and are the\[pth,\,\,qth\]and\[rth\]terms of a geometric progression respectively, then the value of the determinant \[\left| \begin{matrix} \log x & p & 1 \\ \log y & q & 1 \\ \log z & r & 1 \\ \end{matrix} \right|\] equals
A)
\[\log xyz\]
done
clear
B)
\[(p-1)(q-1)(r-1)\]
done
clear
C)
\[pqr\]
done
clear
D)
\[0\]
done
clear
View Answer play_arrow
question_answer 138) If\[\left[ \begin{matrix} 1 & -1 & x \\ 1 & x & 1 \\ x & -1 & 1 \\ \end{matrix} \right]\]has no inverse, then the real value of x is
A)
2
done
clear
B)
3
done
clear
C)
0
done
clear
D)
1
done
clear
View Answer play_arrow
question_answer 139) If\[\alpha \]and\[\beta \]are the roots of\[{{x}^{2}}-2x+4=0\], then the value of\[{{\alpha }^{6}}+{{\beta }^{6}}\]is
A)
32
done
clear
B)
64
done
clear
C)
128
done
clear
D)
256
done
clear
View Answer play_arrow
question_answer 140) The locus of z satisfying the inequality \[\left| \frac{z+2i}{2z+i} \right|<1\], where\[z=x+iy\], is
A)
\[{{x}^{2}}+{{y}^{2}}<1\]
done
clear
B)
\[{{x}^{2}}-{{y}^{2}}<1\]
done
clear
C)
\[{{x}^{2}}+{{y}^{2}}>1\]
done
clear
D)
\[2{{x}^{2}}+3{{y}^{2}}<1\]
done
clear
View Answer play_arrow
question_answer 141) If n is an integer which leaves remainder one when divided by three, then\[{{(1+\sqrt{3}i)}^{n}}+{{(1-\sqrt{3}i)}^{n}}\]equals
A)
\[-{{2}^{n+1}}\]
done
clear
B)
\[{{2}^{n+1}}\]
done
clear
C)
\[-{{(-2)}^{n}}\]
done
clear
D)
\[-{{2}^{n}}\]
done
clear
View Answer play_arrow
question_answer 142) The period of\[{{\sin }^{4}}x+{{\cos }^{4}}x\]is
A)
\[\frac{{{\pi }^{4}}}{2}\]
done
clear
B)
\[\frac{{{\pi }^{2}}}{2}\]
done
clear
C)
\[\frac{\pi }{4}\]
done
clear
D)
\[\frac{\pi }{2}\]
done
clear
View Answer play_arrow
question_answer 143) \[\frac{\cos x}{\cos (x-2y)}=\lambda \Rightarrow \tan (x-y)\tan y\]is equal to
A)
\[\frac{1+\lambda }{1-\lambda }\]
done
clear
B)
\[\frac{1-\lambda }{1+\lambda }\]
done
clear
C)
\[\frac{\lambda }{1+\lambda }\]
done
clear
D)
\[\frac{\lambda }{1-\lambda }\]
done
clear
View Answer play_arrow
question_answer 144) \[\cos A\cos 2A\cos 4A...\cos {{2}^{n-1}}A\]equals
A)
\[\frac{\sin {{2}^{n}}A}{{{2}^{n}}\sin A}\]
done
clear
B)
\[\frac{{{2}^{n}}\sin {{2}^{n}}A}{\sin A}\]
done
clear
C)
\[\frac{{{2}^{n}}\sin A}{\sin {{2}^{n}}A}\]
done
clear
D)
\[\frac{\sin A}{{{2}^{n}}\sin {{2}^{n}}A}\]
done
clear
View Answer play_arrow
question_answer 145) If\[3\cos x\ne 2\sin x\], then the general solution of\[{{\sin }^{2}}x-\cos 2x=2-\sin 2x\]is
A)
\[n\pi +{{(-1)}^{n}}\frac{\pi }{2},\,\,n\in Z\]
done
clear
B)
\[\frac{n\pi }{2},\,\,n\in Z\]
done
clear
C)
\[(4n\pm 1)\frac{\pi }{2},\,\,n\in Z\]
done
clear
D)
\[(2n-1)\pi ,\,\,n\in Z\]
done
clear
View Answer play_arrow
question_answer 146) \[{{\cos }^{-1}}\left( \frac{-1}{2} \right)-2{{\sin }^{-1}}\left( \frac{1}{2} \right)+3{{\cos }^{-1}}\left( \frac{-1}{\sqrt{2}} \right)\]\[-4{{\tan }^{-1}}(-1)\]equals
A)
\[\frac{19\pi }{12}\]
done
clear
B)
\[\frac{35\pi }{12}\]
done
clear
C)
\[\frac{47\pi }{12}\]
done
clear
D)
\[\frac{43\pi }{12}\]
done
clear
View Answer play_arrow
question_answer 147) \[{{\sinh }^{-1}}2+{{\sinh }^{-1}}3=x\Rightarrow \cosh x\]is equal to
A)
\[\frac{1}{2}(3\sqrt{5}+2\sqrt{10})\]
done
clear
B)
\[\frac{1}{2}(3\sqrt{5}-2\sqrt{10})\]
done
clear
C)
\[\frac{1}{2}(12+2\sqrt{50})\]
done
clear
D)
\[\frac{1}{2}(12-2\sqrt{50})\]
done
clear
View Answer play_arrow
question_answer 148) In any\[\Delta \,\,ABC\],\[a(b\cos C-c\cos B)\]equals
A)
\[{{b}^{2}}+{{c}^{2}}\]
done
clear
B)
\[{{b}^{2}}-{{c}^{2}}\]
done
clear
C)
\[\frac{1}{b}+\frac{1}{c}\]
done
clear
D)
\[\frac{1}{{{b}^{2}}}-\frac{1}{{{c}^{2}}}\]
done
clear
View Answer play_arrow
question_answer 149) In a\[\Delta \,\,ABC\] \[\frac{(a+b+c)(b+c-a)(c+a-b)(a+b-c)}{4{{b}^{2}}{{c}^{2}}}\]equals
A)
\[{{\cos }^{2}}A\]
done
clear
B)
\[{{\cos }^{2}}B\]
done
clear
C)
\[{{\sin }^{2}}A\]
done
clear
D)
\[{{\sin }^{2}}B\]
done
clear
View Answer play_arrow
question_answer 150) P is a point on the segment joining the feet of two vertical poles of heights\[a\]and\[b\]. The angles of elevation of the tops of the poles from P are\[{{45}^{o}}\]each. Then, the square of the distance between the tops of the poles is
A)
\[\frac{{{a}^{2}}+{{b}^{2}}}{2}\]
done
clear
B)
\[{{a}^{2}}+{{b}^{2}}\]
done
clear
C)
\[2({{a}^{2}}+{{b}^{2}})\]
done
clear
D)
\[4({{a}^{2}}+{{b}^{2}})\]
done
clear
View Answer play_arrow
question_answer 151) In a quadrilateral\[ABCD\], the point P divides \[DC\]in the ratio\[1:2\]and\[Q\]is the midpoint of\[AC\]. If\[\overrightarrow{\mathbf{AB}}+2\overrightarrow{\mathbf{AD}}+\overrightarrow{\mathbf{BC}}-2\overrightarrow{\mathbf{DC}}=k\overrightarrow{\mathbf{PQ}}\], then\[k\]is equal to
A)
-6
done
clear
B)
-4
done
clear
C)
6
done
clear
D)
4
done
clear
View Answer play_arrow
question_answer 152) The angle between the lines whose direction cosines satisfy the equations\[l+m+n=0\],\[{{l}^{2}}+{{m}^{2}}-{{n}^{2}}=0\]is
A)
\[\frac{\pi }{6}\]
done
clear
B)
\[\frac{\pi }{4}\]
done
clear
C)
\[\frac{\pi }{3}\]
done
clear
D)
\[\frac{\pi }{2}\]
done
clear
View Answer play_arrow
question_answer 153) If\[\overset{\to }{\mathop{\mathbf{a}}}\,=-\widehat{\mathbf{i}}+\widehat{\mathbf{j}}+2\widehat{\mathbf{k}}\], \[\mathbf{\vec{b}=2\hat{i}-\hat{j}-\hat{k}}\] and\[\overset{\to }{\mathop{\mathbf{c}}}\,=-2\widehat{\mathbf{i}}+\widehat{\mathbf{j}}+3\widehat{\mathbf{k}}\], then the angle between\[2\overrightarrow{\mathbf{a}}-\overrightarrow{\mathbf{c}}\]and\[\overrightarrow{\mathbf{a}}+\overrightarrow{\mathbf{b}}\]is
A)
\[\frac{\pi }{4}\]
done
clear
B)
\[\frac{\pi }{3}\]
done
clear
C)
\[\frac{\pi }{2}\]
done
clear
D)
\[\frac{3\pi }{2}\]
done
clear
View Answer play_arrow
question_answer 154) If\[{{m}_{1}},\,\,{{m}_{2}},\,\,{{m}_{3}}\]and\[{{m}_{4}}\]are respectively the magnitudes of the vectors \[{{\overrightarrow{\mathbf{a}}}_{1}}=2\widehat{\mathbf{i}}-\widehat{\mathbf{j}}+\widehat{\mathbf{k}},\,\,\,\,{{\overrightarrow{\mathbf{a}}}_{2}}=3\widehat{\mathbf{i}}-4\widehat{\mathbf{j}}-4\widehat{\mathbf{k}}\] \[{{\overrightarrow{\mathbf{a}}}_{3}}=\widehat{\mathbf{i}}+\widehat{\mathbf{j}}-\widehat{\mathbf{k}}\]and\[{{\overrightarrow{\mathbf{a}}}_{4}}=-\widehat{\mathbf{i}}+3\widehat{\mathbf{j}}+\widehat{\mathbf{k}}\] then the correct order of\[{{m}_{1}},\,\,{{m}_{2}},\,\,{{m}_{3}}\]and\[{{m}_{4}}\]is
A)
\[{{m}_{3}}<{{m}_{1}}<{{m}_{4}}<{{m}_{2}}\]
done
clear
B)
\[{{m}_{3}}<{{m}_{1}}<{{m}_{2}}<{{m}_{4}}\]
done
clear
C)
\[{{m}_{3}}<{{m}_{4}}<{{m}_{1}}<{{m}_{2}}\]
done
clear
D)
\[{{m}_{3}}<{{m}_{4}}<{{m}_{2}}<{{m}_{1}}\]
done
clear
View Answer play_arrow
question_answer 155) Suppose\[\overrightarrow{\mathbf{a}}=\lambda \widehat{\mathbf{i}}-7\widehat{\mathbf{j}}+3\widehat{\mathbf{k}}\]. If\[\overrightarrow{\mathbf{b}}=\lambda \widehat{\mathbf{i}}+2\lambda \widehat{\mathbf{k}}\]. If the angle between\[\overrightarrow{\mathbf{a}}\]and\[\overrightarrow{\mathbf{b}}\]is greater than\[{{90}^{o}}\], then\[\lambda \]satisfies the inequality
A)
\[-7<\lambda <1\]
done
clear
B)
\[\lambda >1\]
done
clear
C)
\[1<\lambda <7\]
done
clear
D)
\[-5<\lambda <1\]
done
clear
View Answer play_arrow
question_answer 156) The volume of the tetrahedron having the edges\[\widehat{\mathbf{i}}+2\widehat{\mathbf{j}}-\widehat{\mathbf{k}},\,\,\widehat{\mathbf{i}}+\widehat{\mathbf{j}}+\widehat{\mathbf{k}},\,\,\widehat{\mathbf{i}}-\widehat{\mathbf{j}}+\lambda \widehat{\mathbf{k}}\]as coterminous, is\[\frac{2}{3}\]cubic unit. Then\[\lambda \]equals
A)
1
done
clear
B)
2
done
clear
C)
3
done
clear
D)
4
done
clear
View Answer play_arrow
question_answer 157) If\[A\]and\[B\]are events of a random experiment such that\[P(A\cup B)=\frac{4}{5},\,\,P(\bar{A}\cup \bar{B})=\frac{7}{10}\]and\[P(B)=\frac{2}{5}\], then\[P(A)\]equals
A)
\[\frac{9}{10}\]
done
clear
B)
\[\frac{8}{10}\]
done
clear
C)
\[\frac{7}{10}\]
done
clear
D)
\[\frac{3}{5}\]
done
clear
View Answer play_arrow
question_answer 158) The probability of choosing randomly a number\[c\]from the set\[\{1,\,\,2,\,\,3,...,\,\,9\}\]such that the quadratic equation\[{{x}^{2}}+4x+c=0\]has real roots is
A)
\[\frac{1}{9}\]
done
clear
B)
\[\frac{2}{9}\]
done
clear
C)
\[\frac{3}{9}\]
done
clear
D)
\[\frac{4}{9}\]
done
clear
View Answer play_arrow
question_answer 159)
Suppose that\[{{E}_{1}}\]and\[{{E}_{2}}\]are two events of\[a\]random experiment such that\[P({{E}_{1}})=\frac{1}{4}\],\[P({{E}_{2}}/{{E}_{1}})=\frac{1}{2}\] and\[P({{E}_{1}}/{{E}_{2}})=\frac{1}{4}\], observe the lists given below
List-I
List-II
(A) \[P({{E}_{2}})\]
(i) 1/4
(B) \[P({{E}_{1}}\cup {{E}_{2}})\]
(ii) 5/8
(C) \[P({{\bar{E}}_{1}}/{{\bar{E}}_{2}})\]
(iii) 1/8
(D)\[P({{E}_{1}}/{{\bar{E}}_{2}})\]
(iv) 1/2
(v) 3/8
(vi) 3/4
The correct matching of the List I from the List II is
A)
A-(ii) B-(iii) C-(vi) D-(i)
done
clear
B)
A-(iv) B-(v) C-(vi) D-(i)
done
clear
C)
A-(iv) B-(ii) C-(vi) D-(i)
done
clear
D)
A-(i) B-(ii) C-(iii) D-(iv)
done
clear
View Answer play_arrow
question_answer 160)
If\[m\]and\[{{\sigma }^{2}}\]are the mean and variance of the random variable, whose distribution is given by \[X=x\] 0 1 2 3 \[P(X=x)\] \[\frac{1}{3}\] \[\frac{1}{2}\] 0 \[\frac{1}{6}\]
Then
A)
\[m={{\sigma }^{2}}=2\]
done
clear
B)
\[m=1,\,\,{{\sigma }^{2}}=2\]
done
clear
C)
\[m={{\sigma }^{2}}=1\]
done
clear
D)
\[m=2,\,\,{{\sigma }^{2}}=1\]
done
clear
View Answer play_arrow
question_answer 161) If\[X\]is a binomial variate with the range\[\{0,\,\,1,\,\,2,\,\,3,\,\,4,\,\,5,\,\,6\}\]and\[P(X=2)=4P(X=4),\]then the parameter\[p\]of\[X\]is
A)
\[\frac{1}{3}\]
done
clear
B)
\[\frac{1}{2}\]
done
clear
C)
\[\frac{2}{3}\]
done
clear
D)
\[\frac{3}{4}\]
done
clear
View Answer play_arrow
question_answer 162) The transformed equation of\[{{x}^{2}}+{{y}^{2}}={{r}^{2}}\]when the axes are rotated through an angle \[{{36}^{o}}\]is
A)
\[\sqrt{5}{{X}^{2}}-4XY+{{Y}^{2}}={{r}^{2}}\]
done
clear
B)
\[{{X}^{2}}+2XY-\sqrt{5}{{Y}^{2}}={{r}^{2}}\]
done
clear
C)
\[{{X}^{2}}-{{Y}^{2}}={{r}^{2}}\]
done
clear
D)
\[{{X}^{2}}+{{Y}^{2}}={{r}^{2}}\]
done
clear
View Answer play_arrow
question_answer 163) The area (in square unit) of the circle which touches the lines\[4x+3y=15\]and\[4x+3y=5\] is
A)
\[4\pi \]
done
clear
B)
\[3\pi \]
done
clear
C)
\[2\pi \]
done
clear
D)
\[\pi \]
done
clear
View Answer play_arrow
question_answer 164) The point on the line\[3x+4y=5\]which is equidistant from (1, 2) and (3, 4) is
A)
(7, -4)
done
clear
B)
(15,-10)
done
clear
C)
(1/7, 8/7)
done
clear
D)
(0, 5/4)
done
clear
View Answer play_arrow
question_answer 165) The equation of the straight line perpendicular to the straight line\[3x+2y=0\]and passing through the point of intersection of the lines\[x+3y-1=0\]and\[x-2y+4=0\]is
A)
\[2x-3y+1=0\]
done
clear
B)
\[2x-3y+3=0\]
done
clear
C)
\[2x-3y+5=0\]
done
clear
D)
\[2x-3y+7=0\]
done
clear
View Answer play_arrow
question_answer 166) The value of\[\lambda \]with\[|\lambda |\,\,<16\]such that\[2{{x}^{2}}-10xy+12{{y}^{2}}+5x+\lambda y-3=0\]represents a pair of straight lines, is
A)
-10
done
clear
B)
-9
done
clear
C)
10
done
clear
D)
9
done
clear
View Answer play_arrow
question_answer 167) The area (in square unit) of the triangle formed by\[x+y+1=0\]and the pair of straight lines\[{{x}^{2}}-3xy+2{{y}^{2}}=0\]is
A)
\[\frac{7}{12}\]
done
clear
B)
\[\frac{5}{12}\]
done
clear
C)
\[\frac{1}{12}\]
done
clear
D)
\[\frac{1}{6}\]
done
clear
View Answer play_arrow
question_answer 168) The pairs of straight lines\[{{x}^{2}}-3xy+2{{y}^{2}}=0\]and\[{{x}^{2}}-3xy+2{{y}^{2}}+x-2=0\]form a
A)
square but not rhombus
done
clear
B)
rhombus
done
clear
C)
parallelogram
done
clear
D)
rectangle but not a square
done
clear
View Answer play_arrow
question_answer 169) The equations of the circle which pass through the origin and makes intercepts of lengths 4 and 8 on the\[x\]and y-axes respectively are
A)
\[{{x}^{2}}+{{y}^{2}}\pm 4x\pm 8y=0\]
done
clear
B)
\[{{x}^{2}}+{{y}^{2}}\pm 2x\pm 4y=0\]
done
clear
C)
\[{{x}^{2}}+{{y}^{2}}\pm 8x\pm 16y=0\]
done
clear
D)
\[{{x}^{2}}+{{y}^{2}}\pm x\pm y=0\]
done
clear
View Answer play_arrow
question_answer 170) The locus of centre of a circle which passes through the origin and cuts off a length of 4 unit from the line\[x=3\]is
A)
\[{{y}^{2}}+6x=0\]
done
clear
B)
\[{{y}^{2}}+6x=13\]
done
clear
C)
\[{{y}^{2}}+6x=10\]
done
clear
D)
\[{{x}^{2}}+6y=13\]
done
clear
View Answer play_arrow
question_answer 171) The diameters of a circle are along\[2x+y-7=0\]and\[x+3y-11=0\]. Then, the equation of this circle, which also passes through (5, 7), is
A)
\[{{x}^{2}}+{{y}^{2}}-4x-6y-16=0\]
done
clear
B)
\[{{x}^{2}}+{{y}^{2}}-4x-6y-20=0\]
done
clear
C)
\[{{x}^{2}}+{{y}^{2}}-4x-6y-12=0\]
done
clear
D)
\[{{x}^{2}}+{{y}^{2}}+4x+6y-12=0\]
done
clear
View Answer play_arrow
question_answer 172) The point (3,-4) lies on both the circles\[{{x}^{2}}+{{y}^{2}}-2x+8y+13=0\]and\[{{x}^{2}}+{{y}^{2}}-4x+6y+11=0\]. Then, the angle between the circles is
A)
\[{{60}^{o}}\]
done
clear
B)
\[{{\tan }^{-1}}\left( \frac{1}{2} \right)\]
done
clear
C)
\[{{\tan }^{-1}}\left( \frac{3}{5} \right)\]
done
clear
D)
\[{{135}^{o}}\]
done
clear
View Answer play_arrow
question_answer 173) The equation of the circle which passes through the origin and cuts orthogonally each of the circles\[{{x}^{2}}+{{y}^{2}}-6x+8=0\]and\[{{x}^{2}}+{{y}^{2}}-2x-2y=7\]is
A)
\[3{{x}^{2}}+3{{y}^{2}}-8x-13y=0\]
done
clear
B)
\[3{{x}^{2}}+3{{y}^{2}}-8x+29y=0\]
done
clear
C)
\[3{{x}^{2}}+3{{y}^{2}}+8x+29y=0\]
done
clear
D)
\[3{{x}^{2}}+3{{y}^{2}}-8x-29y=0\]
done
clear
View Answer play_arrow
question_answer 174) The number of normals drawn to the parabola \[{{y}^{2}}=4x\]from the point (1, 0) is
A)
0
done
clear
B)
1
done
clear
C)
2
done
clear
D)
3
done
clear
View Answer play_arrow
question_answer 175) If the distance between the foci of an ellipse is 6 and the length of the minor axis is 8, then the eccentricity is .
A)
\[\frac{1}{\sqrt{5}}\]
done
clear
B)
\[\frac{1}{2}\]
done
clear
C)
\[\frac{3}{5}\]
done
clear
D)
\[\frac{4}{5}\]
done
clear
View Answer play_arrow
question_answer 176) If the circle\[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\]intersects the hyperbola\[xy={{c}^{2}}\]in four points\[({{x}_{i}},\,\,{{y}_{i}})\], for \[i=1,\,\,2,\,\,3\]and 4, then\[{{y}_{1}}+{{y}_{2}}+{{y}_{3}}+{{y}_{4}}\] equals
A)
0
done
clear
B)
\[c\]
done
clear
C)
\[a\]
done
clear
D)
\[{{c}^{4}}\]
done
clear
View Answer play_arrow
question_answer 177) The midpoint of the chord\[4x-3y=5\]of the hyperbola\[2{{x}^{2}}-3{{y}^{2}}=12\]is
A)
\[\left( 0,\,\,-\frac{5}{3} \right)\]
done
clear
B)
\[(2,\,\,1)\]
done
clear
C)
\[\left( \frac{5}{4},\,\,0 \right)\]
done
clear
D)
\[\left( \frac{11}{4},\,\,2 \right)\]
done
clear
View Answer play_arrow
question_answer 178) The eccentricity of the conic\[\frac{5}{r}=2+3\cos \theta +4\sin \theta \]is
A)
\[\frac{1}{2}\]
done
clear
B)
\[1\]
done
clear
C)
\[\frac{3}{2}\]
done
clear
D)
\[\frac{5}{2}\]
done
clear
View Answer play_arrow
question_answer 179) The perimeter of the triangle with vertices at \[(1,\,\,0,\,\,0),\,\,(0,\,\,1,\,\,0)\]and\[(0,\,\,0,\,\,1)\]is
A)
\[3\]
done
clear
B)
\[2\]
done
clear
C)
\[2\sqrt{2}\]
done
clear
D)
\[3\sqrt{2}\]
done
clear
View Answer play_arrow
question_answer 180) If a line in the space makes angle\[\alpha \],\[\beta \]and\[\gamma \] with the coordinate axes, then\[\cos 2\alpha +\cos 2\beta +\cos 2\gamma +{{\sin }^{2}}\alpha +{{\sin }^{2}}\beta \]\[+{{\sin }^{2}}\gamma \] equals
A)
\[-1\]
done
clear
B)
\[0\]
done
clear
C)
\[1\]
done
clear
D)
\[2\]
done
clear
View Answer play_arrow
question_answer 181) The image of the point (3, 2, 1) in the plane\[2x-y+3z=7\]is
A)
(1, 2, 3)
done
clear
B)
(2, 3, 1)
done
clear
C)
(3, 2, 1)
done
clear
D)
(2, 1, 3)
done
clear
View Answer play_arrow
question_answer 182) The radius of the sphere\[{{x}^{2}}+{{y}^{2}}+{{z}^{2}}=12x+4y+3z\]is
A)
\[\frac{13}{2}\]
done
clear
B)
13
done
clear
C)
26
done
clear
D)
52
done
clear
View Answer play_arrow
question_answer 183) \[\underset{x\to \infty }{\mathop{\lim }}\,{{\left( \frac{x+5}{x+2} \right)}^{x+3}}\]equals
A)
\[e\]
done
clear
B)
\[{{e}^{2}}\]
done
clear
C)
\[{{e}^{3}}\]
done
clear
D)
\[{{e}^{5}}\]
done
clear
View Answer play_arrow
question_answer 184) If\[f:R\to R\]is denned by \[f(x)=\left\{ \begin{matrix} \frac{2\sin x-\sin x}{2x\cos x}, & if\,\,x\ne 0 \\ a, & if\,\,x=0 \\ \end{matrix} \right.\] then the value of a so that/is continuous at 0 is
A)
2
done
clear
B)
1
done
clear
C)
-1
done
clear
D)
0
done
clear
View Answer play_arrow
question_answer 185) \[x=\frac{1-\sqrt{y}}{1+\sqrt{y}}\Rightarrow \frac{dy}{dx}\]is equal to
A)
\[\frac{4}{{{(x+1)}^{2}}}\]
done
clear
B)
\[\frac{4(x-1)}{{{(1+x)}^{3}}}\]
done
clear
C)
\[\frac{x-1}{{{(1+x)}^{3}}}\]
done
clear
D)
\[\frac{4}{{{(x+1)}^{3}}}\]
done
clear
View Answer play_arrow
question_answer 186) \[x={{\cos }^{-1}}\left( \frac{1}{\sqrt{1+{{t}^{2}}}} \right),\,\,y={{\sin }^{-1}}\left( \frac{t}{\sqrt{1+{{t}^{2}}}} \right)\Rightarrow \frac{dy}{dx}\] is equal to
A)
0
done
clear
B)
\[\tan t\]
done
clear
C)
1
done
clear
D)
\[\sin t\cos t\]
done
clear
View Answer play_arrow
question_answer 187) \[\frac{d}{dx}\left[ a{{\tan }^{-1}}x+b\log \left( \frac{x-1}{x+1} \right) \right]=\frac{1}{{{x}^{4}}-1}\] \[\Rightarrow \,\,a-2b\]is equal to
A)
1
done
clear
B)
-1
done
clear
C)
0
done
clear
D)
2
done
clear
View Answer play_arrow
question_answer 188) \[y={{e}^{a{{\sin }^{-1}}x}}\Rightarrow (1-{{x}^{2}}){{y}_{n+2}}-(2n+1)x{{y}_{n+1}}\]is equal to
A)
\[-({{n}^{2}}+{{a}^{2}}){{y}_{n}}\]
done
clear
B)
\[({{n}^{2}}-{{a}^{2}}){{y}_{n}}\]
done
clear
C)
\[({{n}^{2}}+{{a}^{2}}){{y}_{n}}\]
done
clear
D)
\[-({{n}^{2}}-{{a}^{2}}){{y}_{n}}\]
done
clear
View Answer play_arrow
question_answer 189) There is an error of\[\pm 0.04\,\,cm\]in the measurement of the diameter of a sphere. When the radius is\[10\,\,cm\], the percentage error in the volume of the sphere is
A)
\[\pm 1.2\]
done
clear
B)
\[\pm 1.0\]
done
clear
C)
\[\pm 0.8\]
done
clear
D)
\[\pm 0.6\]
done
clear
View Answer play_arrow
question_answer 190) The function\[f(x)={{x}^{3}}+a{{x}^{2}}+bx+c,\,\,{{a}^{2}}\le 3b\] has
A)
one maximum value
done
clear
B)
one minimum value
done
clear
C)
no extreme value
done
clear
D)
one maximum and one minimum value
done
clear
View Answer play_arrow
question_answer 191) . The maximum value of\[\frac{\log x}{x},\,\,0<x<\infty \]is
A)
\[\infty \]
done
clear
B)
\[e\]
done
clear
C)
\[1\]
done
clear
D)
\[{{e}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 192) \[z=\tan (y+ax)+\sqrt{y-ax}\Rightarrow \,\,{{z}_{xx}}-{{a}^{2}}{{z}_{yy}}\]is equal to
A)
0
done
clear
B)
2
done
clear
C)
\[{{z}_{x}}+{{z}_{y}}\]
done
clear
D)
\[{{z}_{x}}{{z}_{y}}\]
done
clear
View Answer play_arrow
question_answer 193) \[\int{\frac{dx}{(x+1)\sqrt{4x+3}}}\]is equal to
A)
\[{{\tan }^{-1}}\sqrt{4x+3}+c\]
done
clear
B)
\[3{{\tan }^{-1}}\sqrt{4x+3}+c\]
done
clear
C)
\[2{{\tan }^{-1}}\sqrt{4x+3}+c\]
done
clear
D)
\[4{{\tan }^{-1}}\sqrt{4x+3}+c\]
done
clear
View Answer play_arrow
question_answer 194) \[\int{\left( \frac{2-\sin 2x}{1-\cos 2x} \right)}\,{{e}^{x}}\]is equal to
A)
\[-{{e}^{x}}\cot x+c\]
done
clear
B)
\[{{e}^{x}}\cot x+c\]
done
clear
C)
\[2{{e}^{x}}\cot x+c\]
done
clear
D)
\[-2{{e}^{x}}+\cot x+c\]
done
clear
View Answer play_arrow
question_answer 195) \[{{I}_{n}}=\int{{{\sin }^{n}}}x\,\,dx\], then\[n{{I}_{n}}-(n-1){{I}_{n-2}}\]equals
A)
\[{{\sin }^{n-1}}x\cos x\]
done
clear
B)
\[{{\cos }^{n-1}}x\sin x\]
done
clear
C)
\[-{{\sin }^{n-1}}x\cos x\]
done
clear
D)
\[-{{\cos }^{n-1}}x\sin x\]
done
clear
View Answer play_arrow
question_answer 196) \[\int_{0}^{\pi }{\frac{1}{1+\sin x}dx}\]is equal to
A)
1
done
clear
B)
2
done
clear
C)
-1
done
clear
D)
-2
done
clear
View Answer play_arrow
question_answer 197) The line\[x=\frac{\pi }{4}\]divides the area of the region bounded by\[y=\sin x,\,\,y=\cos x\]and x-axis\[\left( 0\le x\le \frac{\pi }{2} \right)\]into two regions of areas\[{{A}_{1}}\]and\[{{A}_{2}}\]. Then\[{{A}_{1}},\,\,{{A}_{2}}\]equals
A)
4 : 1
done
clear
B)
3 : 1
done
clear
C)
2 : 1
done
clear
D)
1 : 1
done
clear
View Answer play_arrow
question_answer 198)
The velocity of a particle which starts from rest is given by the following table. t (in second) 0 2 4 6 8 10 v ( in m/s) 0 12 16 20 35 60
The total distance travelled (in metre) by the particles in 10 s, using Trapezoidal rule is given by
A)
113
done
clear
B)
226
done
clear
C)
143
done
clear
D)
246
done
clear
View Answer play_arrow
question_answer 199) The solution of the differential equation\[\frac{dy}{dx}=\sin (x+y)\tan (x+y)-1\]is
A)
\[\cos ec(x+y)+\tan (x+y)=x+c\]
done
clear
B)
\[x+\cos ec(x+y)=c\]
done
clear
C)
\[x+\tan (x+y)=c\]
done
clear
D)
\[x+\sec (x+y)=c\]
done
clear
View Answer play_arrow
question_answer 200) The differential equation of the family\[y=a{{e}^{x}}+bx\,\,{{e}^{x}}+c{{x}^{2}}{{e}^{x}}\]of curves, where\[a,\,\,b,\,\,c\]are arbitrary constants, is
A)
\[y+3y+3y+y=0\]
done
clear
B)
\[y+3y-3y-y=0\]
done
clear
C)
\[y-3y-3y+y=0\]
done
clear
D)
\[y-3y+3y-y=0\]
done
clear
View Answer play_arrow
question_answer 201) INTREPID
A)
Coward
done
clear
B)
Fearless
done
clear
C)
Selfish
done
clear
D)
Ugly
done
clear
View Answer play_arrow
question_answer 202) LAMENTABLE
A)
Deplorable
done
clear
B)
Contemptible
done
clear
C)
Remorseful
done
clear
D)
Scornful
done
clear
View Answer play_arrow
question_answer 203) DEFT
A)
Skilful
done
clear
B)
Vigorous
done
clear
C)
Swift
done
clear
D)
Deceitful
done
clear
View Answer play_arrow
question_answer 204) HOARD
A)
Destroy
done
clear
B)
Hide
done
clear
C)
Store
done
clear
D)
Divide
done
clear
View Answer play_arrow
question_answer 205) He is too dull...... the problem.
A)
solves
done
clear
B)
to solve
done
clear
C)
solving
done
clear
D)
to solving
done
clear
View Answer play_arrow
question_answer 206) The speaker drew the attention of the audience ...... the burning issue.
A)
to
done
clear
B)
towards
done
clear
C)
on
done
clear
D)
into
done
clear
View Answer play_arrow
question_answer 207) Its nine oclock ...... and Im still at breakfast.
A)
till
done
clear
B)
yet
done
clear
C)
so
done
clear
D)
already
done
clear
View Answer play_arrow
question_answer 208) Although he is blind, he is very fast ...... calculations.
A)
in
done
clear
B)
with
done
clear
C)
at
done
clear
D)
about
done
clear
View Answer play_arrow
question_answer 209) VIRTUE
A)
Vice
done
clear
B)
Fraud
done
clear
C)
Wickedness
done
clear
D)
Crime
done
clear
View Answer play_arrow
question_answer 210) ZEAL
A)
Hostility
done
clear
B)
Diffidence
done
clear
C)
Apathy
done
clear
D)
Contempt
done
clear
View Answer play_arrow
question_answer 211) AGONY
A)
Enmity
done
clear
B)
Cruelty
done
clear
C)
Abhorrence
done
clear
D)
Ecstasy
done
clear
View Answer play_arrow
question_answer 212) ERUDITE
A)
Professional
done
clear
B)
Immature
done
clear
C)
Unimaginative
done
clear
D)
Ignorant
done
clear
View Answer play_arrow
question_answer 213) A person who speaks for or supports an idea
A)
Pioneer
done
clear
B)
Adviser
done
clear
C)
Advocate
done
clear
D)
Ideologist
done
clear
View Answer play_arrow
question_answer 214) A man of odd habits
A)
Eccentric
done
clear
B)
Cynical
done
clear
C)
Introvert
done
clear
D)
Moody
done
clear
View Answer play_arrow
question_answer 215) A thing or person behind time
A)
Lazy
done
clear
B)
Sluggish
done
clear
C)
Indolent
done
clear
D)
Antiquated
done
clear
View Answer play_arrow
question_answer 216) One whose attitude is : eat, drink and be merry
A)
Epicurean
done
clear
B)
Cynic
done
clear
C)
Materialistic
done
clear
D)
Stoic
done
clear
View Answer play_arrow
question_answer 217) Older people often stay at home and watch TV because it is cold and dark in winter.
A)
seldom
done
clear
B)
frequently
done
clear
C)
sometimes
done
clear
D)
No improvement
done
clear
View Answer play_arrow
question_answer 218) You must find someone to accompany you to Mumbai
A)
no one
done
clear
B)
everyone
done
clear
C)
anyone
done
clear
D)
No improvement
done
clear
View Answer play_arrow
question_answer 219) No sooner ne reached home than all the villagers gathered at his home to listen to his story.
A)
would he reach
done
clear
B)
did he reach
done
clear
C)
have he reached
done
clear
D)
No improvement
done
clear
View Answer play_arrow
question_answer 220) I wish I was with him.
A)
have been
done
clear
B)
were
done
clear
C)
am
done
clear
D)
No improvement
done
clear
View Answer play_arrow
question_answer 221) Sandstone : Limestone : Coal
A)
They are formed by metamorphic rocks.
done
clear
B)
They are chemical minerals.
done
clear
C)
They are found in river beds.
done
clear
D)
They are formed in sedimentary rocks.
done
clear
View Answer play_arrow
question_answer 222) Sweep : Scrub : Wipe
A)
These are terms connected with rubbing.
done
clear
B)
These are games of cards.
done
clear
C)
These are terms used by motor mechanics.
done
clear
D)
These are terms connected with cleaning.
done
clear
View Answer play_arrow
question_answer 223) Delhi : Agra : Mathura
A)
They have been capitals of the country
done
clear
B)
They have exquisite temples.
done
clear
C)
They have religious background
done
clear
D)
They are situated on the bank of river Yamuna.
done
clear
View Answer play_arrow
question_answer 224) Press : Television : Cinema
A)
They are means of entertainment.
done
clear
B)
They are means of mass media.
done
clear
C)
They give worldwide news.
done
clear
D)
All are public undertakings.
done
clear
View Answer play_arrow
question_answer 225) Comets : Stars : Satellites
A)
They are shining masses-
done
clear
B)
They give out light.
done
clear
C)
They are rotating from left to right
done
clear
D)
They are heavenly bodies.
done
clear
View Answer play_arrow
question_answer 226) Mayagine : Story : Article
A)
Tea : Milk : Sugar
done
clear
B)
Television : Newspaper : Entertainment
done
clear
C)
Bed : Quilt : Pillow
done
clear
D)
Novel : Drama : Literature
done
clear
View Answer play_arrow
question_answer 227) Juice : Orange : Banana
A)
Table : Chair : Wood
done
clear
B)
Fish : Shark : Water
done
clear
C)
Cow : Milk : Curd
done
clear
D)
Ink : Pen : Pencil
done
clear
View Answer play_arrow
question_answer 228) Carnivorous : Tiger : Wolf
A)
Mango : Banana : Fruit
done
clear
B)
Worker: Master: Manager
done
clear
C)
Cat : Cow : Milk
done
clear
D)
Student : Boy : Girl
done
clear
View Answer play_arrow
question_answer 229) Rain : Cloud : Evaporation
A)
Pain : Injury : Accident
done
clear
B)
Cold : Cough : Sneezing
done
clear
C)
Purse : Leather : Tanning
done
clear
D)
Fragrance : Flower : Bud
done
clear
View Answer play_arrow
question_answer 230) Dog : Squirrel : Tail
A)
Cottage : Hut : Palace
done
clear
B)
Fish : Crocodile : Water
done
clear
C)
Horse : OX : Horn
done
clear
D)
Truck : Scooter : Gear
done
clear
View Answer play_arrow
question_answer 231) The five intertwined rings or circles on the Olympic Dag made of white [From left to right] are
A)
Blue, yellow, black, green and red.
done
clear
B)
Yellow, red, green, black and blue.
done
clear
C)
Red, green, black, yellow and blue.
done
clear
D)
Yellow, green black, blue and red.
done
clear
View Answer play_arrow
question_answer 232) The national remote sensing agency is located at
A)
Delhi
done
clear
B)
Hyderabad
done
clear
C)
Bangalore
done
clear
D)
Lucknow
done
clear
View Answer play_arrow
question_answer 233) The Nobel Prize are given to Dec, 10 on die death anniversary of
A)
Linus Pauling
done
clear
B)
Frederic Sanger
done
clear
C)
Alfred Bernard
done
clear
D)
John Bardeen
done
clear
View Answer play_arrow
question_answer 234) The term Gambit is used in
A)
Chess
done
clear
B)
Boning
done
clear
C)
Baseball
done
clear
D)
Polo
done
clear
View Answer play_arrow
question_answer 235) Words fastest missileship INS Prahar was commissioned in
A)
1996
done
clear
B)
1997
done
clear
C)
1998
done
clear
D)
1999
done
clear
View Answer play_arrow
question_answer 236) Nati is the classical dances of
A)
Tamil Nadu
done
clear
B)
Assam
done
clear
C)
Himachal Pradesh
done
clear
D)
Andhra Pradesh
done
clear
View Answer play_arrow
question_answer 237) The headquarter of International Labour Organization is located at
A)
Geneva
done
clear
B)
Paris
done
clear
C)
New York
done
clear
D)
Rome
done
clear
View Answer play_arrow
question_answer 238) The first Indian woman to receive Bharat Rama was
A)
Mother Teresa
done
clear
B)
Mrs. Indira Gandhi
done
clear
C)
Ashapurana devi
done
clear
D)
Aarti Saha
done
clear
View Answer play_arrow
question_answer 239) Kip is the currency of
A)
Kuwait
done
clear
B)
Lebanon
done
clear
C)
Laos
done
clear
D)
Malaysia
done
clear
View Answer play_arrow
question_answer 240) The charter of the United Nations was signed on June 26, 1945 in
A)
San Francisco
done
clear
B)
Washington D.C.
done
clear
C)
Landon
done
clear
D)
Trygue Le
done
clear
View Answer play_arrow