question_answer

Area of the greatest rectangle that can be inscribed in the ellipse\[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\]is

A)  \[2ab\]

B)  \[ab\]

C)  \[\sqrt{ab}\]

D)  \[\frac{a}{b}\]

Correct Answer: A

Solution :

 Let the coordinates of the vertices of the rectangle are \[A(a\cos \theta ,b\sin \theta ),\] \[B(-a\cos \theta ,b\sin \theta ),\]\[C(-a\cos \theta ,-b\sin \theta )\] and \[D(a\cos \theta ,-b\sin \theta )\]. Then, the length of the rectangle\[AB=2a\text{ }cos\theta \]and breadth\[AQ=2b\text{ }\sin \theta \] \[\therefore \]Area of rectangle,   \[A=AB\times AD\] \[=2a\cos \theta .2b\sin \theta \] \[\Rightarrow \] \[A=2ab\sin 2\theta \]        ...(i) \[\therefore \] \[\frac{dA}{d\theta }=2\times 2ab\cos 2\theta \] Put for maxima or minima\[\frac{dA}{d\theta }=0\] \[\Rightarrow \] \[\cos 2\theta =0\] \[\Rightarrow \] \[2\theta =\frac{\pi }{2}\]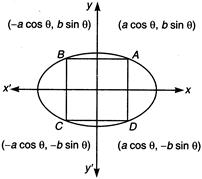 \[\Rightarrow \] \[\theta =\frac{\pi }{4}\] Now, \[\frac{{{d}^{2}}A}{d{{\theta }^{2}}}=-8ab\sin 2\theta \] At          \[\theta =\frac{\pi }{4},\left( \frac{{{d}^{2}}A}{d{{\theta }^{2}}} \right)<0\] \[\therefore \]At\[\theta =\frac{\pi }{4},\]area will be maximum. \[\therefore \]Maximum area of the rectangle \[=2ab\sin 2\left( \frac{\pi }{4} \right)=2ab\] Alternate Method From Eq. (i) \[A=2ab\sin 2\theta \] Since max \[(\sin 2\theta )=1\] \[\therefore \] \[{{A}_{\max }}=2ab\]