question_answer

The equation of perpendicular bisectors of sides AB and AC of a\[\Delta ABC\]are\[x-y+5=0\]and\[x+2y=0,\]respectively. If the coordinates of vertex A are\[(1,-2),\]the equation of BC is

A)  \[14x+23y-40=0\]

B)  \[14x-23y+40=0\]

C)  \[23x+14y-40=0\]

D)  \[23x-14y+40=0\]

Correct Answer: A

Solution :

Let\[B({{x}_{1}},{{y}_{1}})\]and\[C({{x}_{2}},{{y}_{2}})\]be two vertices and\[P\left( \frac{{{x}_{1}}+1}{2},\frac{{{y}_{1}}-2}{2} \right)\]lies on perpendicular bisector\[x-y+5=0\].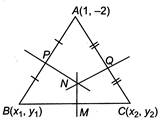 \[\therefore \] \[\frac{{{x}_{1}}+1}{2}-\frac{{{y}_{1}}-2}{2}=-5\] \[\Rightarrow \] \[{{x}_{1}}-{{y}_{1}}=-13\]         ...(i) Also, PAT is perpendicular to AB. \[\therefore \] \[\frac{{{y}_{1}}+2}{{{x}_{1}}-1}\times 1=-1\] \[\Rightarrow \] \[{{y}_{1}}+2=-{{x}_{1}}+1\] \[\Rightarrow \] \[{{x}_{1}}+{{y}_{1}}=-1\] On solving Eqs. (i) and (ii), we get \[{{x}_{1}}=-7,{{y}_{1}}=6\] \[\therefore \]The coordinates of B are\[(-7,\text{ }6)\]. Similarly, the coordinates of C are\[\left( \frac{11}{5},\frac{2}{5} \right)\] Hence, the equation of BC is \[y-6=\frac{\frac{2}{5}-6}{\frac{11}{5}+7}\times (x+7)\] \[\Rightarrow \] \[(y-6)=\frac{-14}{23}\times (x+7)\] \[\Rightarrow \] \[14x+23y-40=0\]