question_answer

The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are \[60{}^\circ \] and \[30{}^\circ \] respectively. Find the height of the tower.

Answer:

Let length of tower is h

In \[\Delta \,ABD\]

\[\tan \,60{}^\circ =\frac{h}{4}\]                                               ?(i)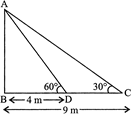

In \[\Delta \,ABC\]

\[\tan \,30{}^\circ =\frac{h}{9}\]

\[\cot (90{}^\circ -30{}^\circ )=\frac{h}{9}\]

\[\cot \,60{}^\circ =\frac{h}{9}\]                                               ?(ii)

Multiplying eq. (i) and (ii), we get

\[\tan \,60{}^\circ .\cot \,60{}^\circ =\frac{h}{4}\times \frac{h}{9}\]

\[1=\frac{{{h}^{2}}}{36}\]

\[h=6\,m\]

Note: In this question, it has not been specified whether two points from tower are taken in same or opposite side we have taken these points on the same side of tower.