question_answer

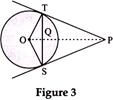
In Fig. 3, from an external point P, two tangents PT and PS are drawn to a circle with centre O and radius r. If \[OP=2r\], show that \[\angle OTS=\angle OST=30{}^\circ \].

Answer:

We have,

\[OP=2r\]

Let                                \[\angle TOP=\theta \]

In \[\Delta \,OTP,\]                      \[\cos \theta =\frac{OT}{OP}=\frac{r}{2r}=\frac{1}{2}\]

\[\because \]                               \[\theta =60{}^\circ \]

Hence,                          \[\angle TOS=2\theta =2\times 60{}^\circ =120{}^\circ \]

In \[\Delta \,TOS\]

\[\angle \,TOS+\angle OTS+\angle OST=180{}^\circ \]

\[120{}^\circ +2\angle OTS=180{}^\circ (\because \,\angle OTS=\angle OST)\]

\[2\angle OTS=180{}^\circ -120{}^\circ \]

\[\angle OTS=30{}^\circ \]

Hence,              \[\angle OTS=\angle OST=30{}^\circ \]              Hence Proved.