question_answer

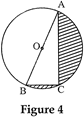
In fig. 4, O is the centre of a circle such that diameter \[AB=13\text{ }cm\] and \[AC=12\,cm.\,\,BC\] is joined Find the area of the shaded region. (Take\[\pi =3.14\])

Answer:

Given, AB is a diameter of length \[13\text{ }cm\]. And \[AC=12\text{ }cm\].

Then, by pythagoras theorem,

\[{{(BC)}^{2}}={{(AB)}^{2}}-{{(AC)}^{2}}\]

\[{{(BC)}^{2}}={{(13)}^{2}}-{{(12)}^{2}}\]

\[BC=\sqrt{169-144}\]

\[BC=\sqrt{25}\]

\[\therefore \]                  \[BC=5\,cm\]

Now, Area of shaded region = Area of semi circle\[\]Area of \[\Delta \text{ }ABC\]

\[=\frac{\pi {{r}^{2}}}{2}-\frac{1}{2}\times BC\times AC\]

\[=\frac{1}{2}\times 3.14\times {{\left( \frac{13}{2} \right)}^{2}}-\frac{1}{2}\times 5\times 12\]

\[=\frac{1.57\times 169}{4}-30\]

\[=66.33-30\]

\[=36.33\,c{{m}^{2}}\]

So, area of shaded region is \[36.33\,\,c{{m}^{2}}\].