question_answer

A man standing on the deck of a ship, which is 10 m above water level, observes the angle of elevation of the top of a hill as \[60{}^\circ \] and the angle of depression of the base of hill as \[30{}^\circ \]. Find the distance of the hill from the ship and the height of the hill.

Answer:

Let AB be the height of water level and CD be the height of hill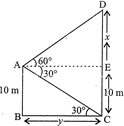

Then,

In \[\Delta \,ABC\] \[\Delta \,ABC\]

\[\tan \,30{}^\circ =\frac{10}{y}\]

\[y=10\sqrt{3}\]                                         ?(i)

In \[\Delta \,ADE\]

\[\tan \,60{}^\circ =\frac{x}{y}\]

\[y=\frac{x}{\sqrt{3}}\]                                           ?(ii)

From (i) and (ii), we get

\[\frac{x}{\sqrt{3}}=10\sqrt{3}\]

\[x=10\times 3=30\,m\]

\[\therefore \] Distance of the hill from this ship is \[10\sqrt{3}\,m\] and the height of the hill is \[30+10=40\text{ }m\].