question_answer

Prove that the lengths of the tangents drawn from an external point to a circle are equal.

Answer:

Given, Two tangents AM and AN are drawn from point A to a circle with centre O.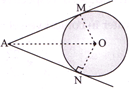

To Prove: \[AM=AN\]

Construction: Join \[OM,ON\] and \[OA\].

Proof: Since, \[AM\] is a tangent and \[OM\] is a radius.

\[\therefore OM\bot AM\]

Similarly,           \[ON\bot AN\]

Now, in \[\Delta \,OMA\] and \[\Delta \,ONA\]

\[OA=OA\]                 (Common)

\[OM=ON\]                 (Radii of the circle)

\[\angle OMA=\angle ONA=90{}^\circ \]

\[\therefore \Delta \,OMA\cong \Delta \,ONA\]         (By RHS congruence)

Hence,              \[AM=AN\]                    Hence Proved.