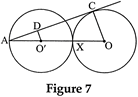
| In Fig. 7, two equal circles, with centres O and O?, touch each other at X. OO? produced meets the circle with centre O? at A. AC is tangent to the circle with centre O, at the point C. O'D is perpendicular AC. Find the value of \[\frac{DO'}{CO}\] . |
 |
Answer:
Given, AC is tangent to the circle with centre O and O'D is perpendicular to AC. then, \[\angle ACO=90{}^\circ \] Also, \[\angle ADO'=90{}^\circ \] \[\angle CAO=\angle DAO'\] (\[\because \] Common angle) \[\therefore \Delta \,AO'D\tilde{\ }\Delta \,AOC\] \[\Rightarrow \frac{AO'}{AO}=\frac{DO'}{CO}\] \[\therefore \frac{AO'}{3.AO'}=\frac{DO'}{CO}\] \[\left( \begin{align} & \because \,AX=2AO' \\ & \,\,\,\,OX=AO' \\ \end{align} \right)\] \[\frac{DO'}{CO}=\frac{1}{3}\]
You need to login to perform this action.
You will be redirected in
3 sec
