question_answer

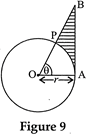
In Fig. 9, is shown a sector OAP of a circle with centre O, containing \[\angle \theta .\text{ }AB\] is perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of shaded region is \[r\left[ \tan \,\theta +\sec \,\theta +\frac{\pi \theta }{180}-1 \right]\]

Answer:

Given, the radius of circle with centre O is r.

\[\angle POA=\theta \].

then, length of the arc \[\overset\frown{PA}=\frac{2\pi r\theta }{360{}^\circ }=\frac{\pi r\theta }{180{}^\circ }\]

And                              \[\tan \theta =\frac{AB}{r}\]

\[AB=r\,\tan \theta \]

And                              \[\sec \theta =\frac{OB}{r}\]

\[OB=r\,\sec \theta \]

Now,                             \[PB=OB-OP\]

\[=r\,\sec \,\theta -r\]

\[\therefore \] Perimeter of shaded region

\[=AB+PB+\overset\frown{PA}\].

\[=r\,\tan \,\theta +r\,\sec \,\theta -r+\frac{\pi r\theta }{180{}^\circ }\]

\[=r\left[ \tan \theta +\sec \theta +\frac{\pi \theta }{180}-1 \right]\]                           Hence Proved.