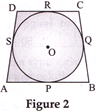
| In Fig. 2, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that \[AB+CD=BC+DA\]. |
 |
Answer:
We have, AB, BC, CD and DA are the tangents touching the circle at P, Q, R and S respectively Now, \[AP=AS,BP=BQ,CR=CQ\] and \[DR=DS\]. On adding we get \[AP+BP+CR+DR=AS+BQ+CQ+DS\] \[AB+CD=AD+BC\] Hence Proved.
You need to login to perform this action.
You will be redirected in
3 sec
