Answer:
Given, a tangent AB at point P of the circle with centre O. To prove: ![]() .
. Construction: Join OQ where Q is a point (other than P) on AB. Proof: Since Q is a point on the tangent AB (other than P). ![]() Q lies outside the circle.
Q lies outside the circle. Let OQ intersect the circle at R. ![]() .
. But ![]() . (Radii of the circle)
. (Radii of the circle) 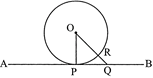
![]() .
. Thus, OP is the shortest distance than any other line segment joining O to any point of AB. But, we know that the shortest distance between a point and a line is the perpendicular distance ![]() Hence Proved.
Hence Proved.
You need to login to perform this action.
You will be redirected in
3 sec
