question_answer

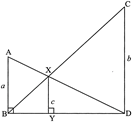
In the figure if \[\angle ABD=\angle XYD=\angle CDB=90{}^\circ .\text{ }AB=a,XY=c\] and \[CD=b\], then prove that\[c\text{ (}a+b)=ab\].

Answer:

To prove: \[c\text{ (}a+b)=ab\]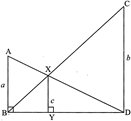

In \[\Delta \text{ }ABD\]& \[\Delta \text{ }DXY\]

\[\angle B=\angle XYD\]              [Each \[90{}^\circ \]]

\[\angle XDY=\angle ADB\]                     [Common]

So by AA similarity

\[\Delta \text{ }DAB\tilde{\ }\Delta \text{ }DXY\]

\[\therefore \]                  \[\frac{DY}{DB}=\frac{XY}{AB}\]

\[DY=\frac{c}{a}(BD)\]                                                  ?(i)

In \[\Delta \text{ }BCD\] & \[\Delta \text{ }BYX\]

\[\angle XYB=\angle D\]                  [Each \[90{}^\circ \]]

\[\angle CBD=\angle XBY\]              [Common]

So by AA similarity,

\[\Delta \text{ }BYX\tilde{\ }\Delta \text{ }BDC\]

\[\frac{BY}{BD}=\frac{XY}{CD}\]

\[BY=\frac{c}{b}(BD)\]                                                   ...(ii)

Adding eq. (i) and eq. (ii)

\[DY+BY=-\,(BD)+\frac{c}{b}(BD)\]

\[BD=BD\left[ \frac{c}{a}+\frac{c}{b} \right]\]

\[\frac{BD}{BD}=\left[ \frac{cb\,\,\,\,\,ca}{ab} \right]\]

\[1=\frac{c(a+b)}{ab}\]

\[c(a+b)=ab\]                                             Hence Proved