| In the figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB = CD. |
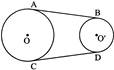 |
Answer:
Construction: Extend AB and CD to meet at a point P 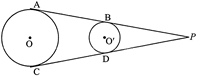
Now, PA and PC are tangents of circle with centre O So \[PA=PC\] ...(i) PB and PD are tangent on circle with centre O? So \[PB=PD\] ...(ii) On subtracting eq. (ii) from eq. (i) \[PA-PR=PCPD\] \[AB=CD\] Hence Proved
You need to login to perform this action.
You will be redirected in
3 sec
