question_answer

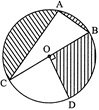
In the given figure, O is the centre of the circle with \[AC=24\text{ }cm,\,\,AB=7\text{ }cm\] and \[\angle BOD=90{}^\circ \]. Find the area of the shaded region.

Answer:

Given, C (O, OB) with \[AC=24\text{ }cm\text{ }AB=7\text{ }cm\] and \[\angle BOD=90{}^\circ \]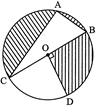

\[\angle CAB=90{}^\circ \] (Angle in semi-circle)

Using pythagoras theorem in \[\Delta \text{ }CAB\]

\[B{{C}^{2}}=A{{C}^{2}}+A{{B}^{2}}\]

\[={{(24)}^{2}}+{{(7)}^{2}}\]

\[=576+49\]

\[=625\]

\[BC=25\,\,cm\]

Radius of circle \[=OB=OD=OC=\frac{25}{2}cm\]

Area of shaded region

= Area of semi-circle with diameter BC\[\]Area of \[\Delta \text{ }CAB\]+Area of sector \[BOD\]

\[=\frac{1}{2}\pi {{\left( \frac{25}{2} \right)}^{2}}-\frac{1}{2}\times 24\times 7+\frac{90}{360}\pi {{\left( \frac{25}{2} \right)}^{2}}\]

\[=\frac{3}{4}\times \frac{22}{7}\times \frac{25}{2}\times \frac{25}{2}-84\]

\[=\frac{20625}{56}-84\]

\[=\frac{20625-4704}{56}\]

\[=\frac{15921}{56}=284.3\,\,c{{m}^{2}}\]     (approx..)