question_answer

Prove that the area of an equilateral triangle described on one side of the square is equal to half the area of the equilateral triangle described on one of its diagonal.

OR

If the area of two similar triangles are equal, prove that they are congruent.

Answer:

Let ABCD be a square with side ?a?.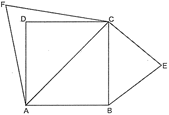

In \[\Delta \text{ }ABC\],

\[A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}\]

\[={{a}^{2}}+{{a}^{2}}\]

\[=2{{a}^{2}}\]

\[AC=\sqrt{2{{a}^{2}}}=\sqrt{2}\,a.\]

Area of equilateral \[\Delta \text{ }BEC\](formed on side BC of square ABCD)

\[=\frac{\sqrt{3}}{4}\times {{(side)}^{2}}\]

\[=\frac{\sqrt{3}}{4}{{a}^{2}}\]                                                                      ...(i)

Area of equilateral \[\Delta \,ACF\](formed on diagonal AC of square ABCD)

\[=\frac{\sqrt{3}}{4}{{(\sqrt{2}\,a)}^{2}}\]

\[=\frac{\sqrt{3}}{4}(2{{a}^{2}})\]

\[=2\frac{\sqrt{3}}{4}{{a}^{2}}\]                                                                    ...(ii)

From eq. (i) and (ii),

\[ar\text{ }\Delta \,ACF=2\times ar\,\Delta \,BCE\]

or         \[ar\text{ (}\Delta BCE)=\frac{1}{2}ar\,(\Delta ACF)\,\]

i.e., area of triangle described on one side of square is half the area of triangle described on its diagonal.

Hence Proved.

OR

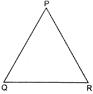
Given,   \[\Delta \text{ }ABC\sim \Delta \text{ }PQR\]

And      \[ar\text{ (}\Delta \text{ }ABC)=ar\text{ (}\Delta \text{ }PQR)\]

To prove:

\[\Delta \,ABC\cong \Delta \,PQR\]

Proof:

Given,   \[\Delta \text{ }ABC\sim \Delta \text{ }PQR\]

\[\therefore \]      \[\frac{ar\,(\Delta \,ABC)}{ar\,(\Delta \,PQR)}=\frac{A{{B}^{2}}}{P{{Q}^{2}}}=\frac{B{{C}^{2}}}{Q{{R}^{2}}}=\frac{A{{C}^{2}}}{P{{R}^{2}}}\]

(Ratio of area of similar triangles is equal to the square of corresponding sides)

But       \[\frac{ar\,(\Delta \,ABC)}{ar\,(\Delta \,PQR)}=1\]                        (Given)

\[\therefore \]        \[\frac{A{{B}^{2}}}{P{{Q}^{2}}}=\frac{B{{C}^{2}}}{Q{{R}^{2}}}=\frac{A{{C}^{2}}}{P{{R}^{2}}}=1\]

So,       \[A{{B}^{2}}=P{{Q}^{2}}\,or\,AB=PQ\]

\[B{{C}^{2}}=Q{{R}^{2}}\,or\,BC=QR\]

\[A{{C}^{2}}=Q{{R}^{2}}\,or\,AC=PR\]

By SSS congruency axiom

\[\Delta \,ABC\cong \Delta \,PQR\]                         Hence Proved.