question_answer

Prove that the lengths of tangents drawn from an external point to a circle are equal.

Answer:

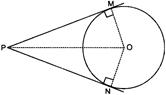
Given: a circle with centre O on which two tangents PM and PN are drawn from an external point P.

To prove:

PM = PN

Construction: Join OM, ON and OP.

Proof: Since tangent and radius are perpendicular at point of contact,

\[\therefore \]    \[\angle OMP=\angle ONP=90{}^\circ \]

In \[\Delta \text{ }POM\]and \[\Delta \text{ }PON\],

\[OM=ON\]                                      (Radii)

\[\angle OMP=\angle ONP\]

\[PO=OP\]                    (Common)

\[\therefore \]      \[\Delta \,OMP\cong \Delta \,ONP\]                            (RHS cong.)

\[\therefore \]        \[PM=PN\]                              (CPCT)

Hence Proved.