question_answer

           

If \[4\text{ }tan\text{ }\theta =3\], evaluate \[\left( \frac{4\,\,\sin \,\,\theta -\cos \,\,\theta +1}{4\,\,\sin \,\,\theta +\cos \,\,\theta -1} \right)\]

OR

If tan \[2A=cot\text{ (}A-18{}^\circ )\], where 2A is an acute angle, find the value of A.

Answer:

Given, \[4\text{ }tan\text{ }\theta =3\],

\[\Rightarrow \] \[\tan \,\theta =\frac{3}{4}\left( =\frac{P}{B} \right)\]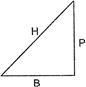

\[P=3K,B=4K,\]

Now,              \[H=\sqrt{{{P}^{2}}+{{B}^{2}}}\]

\[=\sqrt{{{(3K)}^{2}}+{{(4K)}^{2}}}\]

\[=\sqrt{9{{K}^{2}}+16{{K}^{2}}}\]

\[=\sqrt{25{{K}^{2}}}\]

\[\Rightarrow \]            \[H=5K\]

\[\therefore \]      \[\sin \,\theta =\frac{P}{H}=\frac{3K}{5K}=\frac{3}{5}\]

And      \[\cos \,\theta =\frac{B}{H}=\frac{4K}{5K}=\frac{4}{5}\]

Now, \[\frac{4\,\sin \,\theta -\cos \theta +1}{4\,\sin \,\theta +\cos \,\theta -1}=\frac{4\times \frac{3}{5}-\frac{4}{5}+1}{4\times \frac{3}{5}+\frac{4}{5}-1}\]

\[=\frac{\left( \frac{12}{5}-\frac{4}{5}+1 \right)}{\left( \frac{12}{5}+\frac{4}{5}-1 \right)}\]

\[=\frac{\left( \frac{12-4+5}{5} \right)}{\left( \frac{12+4-5}{5} \right)}\]

\[=\frac{13/5}{11/5}\]

\[=\frac{13}{11}\]

OR

Given    \[\tan \,2A=cot\,(A-18{}^\circ )\]

\[\Rightarrow \]   \[\cot \,(90{}^\circ -2A)=cot(A-18{}^\circ )\]

[\[\because \] \[\tan \,\theta =\cot (90{}^\circ -\theta )\]]

\[\Rightarrow \]   \[90{}^\circ -2A=A-18{}^\circ \]

\[\Rightarrow \]   \[90{}^\circ +18{}^\circ =A+2A\]

\[\Rightarrow \]   \[180{}^\circ =3A\]

\[\Rightarrow \]   \[A=\frac{108{}^\circ }{3}\]

\[\Rightarrow \]   \[A=36{}^\circ \]