question_answer

A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in Fig. 3. If the height of the cylinder is 10 cm and its base is of radius 3.5 cm. Find the article.

OR

A heap of rice is in the form of a cone of base diameter 24 m and height 3.5 m. Find the volume of the rice. How much canvas cloth is required to just cover the heap?

Answer:

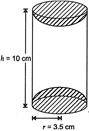
Given, Radius (r) of cylinder = Radius of hemisphere = 3.5 cm.

Total SA of article = CSA of cylinder \[+2\times \] CSA of hemisphere

Height of cylinder, h = 10 cm

TSA  \[=\text{ }2\pi rh+2\times 2\pi {{r}^{2}}\]

\[=2\pi rh+4\pi {{r}^{2}}\]

\[=2\pi r\text{ (}h+2r)\]

\[=2\times \frac{22}{7}\times 3.5(10+2\times 3.5)\]

\[=2\times 22\times 0.5\times (10+7)\]

\[=2\times 11\times 17\]

\[=374\,\,c{{m}^{2}}\]

OR

Base diameter of cone = 24 m.

\[\therefore \] Radius \[r=12\text{ }m\]

Height of cone, \[h=3.5\text{ }m\]

Volume of rice in conical heap

\[=\frac{1}{3}\pi {{r}^{2}}h\]

\[=\frac{1}{3}\times \frac{22}{7}\times 12\times 12\times 3.5\]

\[=528\,{{m}^{3}}\]

Now, slant height, \[l=\sqrt{{{h}^{2}}+{{r}^{2}}}\]

\[=\sqrt{{{(3.5)}^{2}}+{{(12)}^{2}}}\]

\[=\sqrt{12.25+144}\]

\[=\sqrt{156.25}\]

\[=12.5\,m\]

Canvas cloth required to just cover the heap =

CSA of conical heap \[=\pi rl\]

\[=\frac{22}{7}\times 12\times 12.5\]

\[=\frac{3300}{7}{{m}^{2}}\]

\[471.43\,\,{{m}^{2}}\].