question_answer

In an equilateral \[\Delta \text{ }ABC,\text{ }D\]is a point on side BC such that \[BD=\frac{1}{3}BC\]. Prove that \[9{{(AD)}^{2}}\] \[=7{{(AB)}^{2}}\].

OR

Prove that, in a right triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides.

Answer:

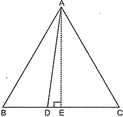
Given, ABC is an equilateral triangle and D is a point on BC such that \[BD=\frac{1}{3}BC\].

To prove:

\[9A{{D}^{2}}=7A{{B}^{2}}\]

Construction: Draw \[AE\bot BC\]

Proof:      \[BD=\frac{1}{3}BC\]                                                            ?(i) (Given)

\[AE\bot BC\]

We know that perpendicular from a vertex of equilateral triangle to the base divides base in two equal parts.

\[\therefore \]      \[BE=EC=\frac{1}{2}BC\]                                             ?(ii)

In \[\Delta \,AEB\],

\[A{{D}^{2}}=A{{E}^{2}}+D{{E}^{2}}\]

(Pythagoras theorem)

Or         \[A{{E}^{2}}=A{{D}^{2}}-D{{E}^{2}}\]                                        ?(iii)

Similarly, In \[\Delta \,AEB\],

\[A{{B}^{2}}=A{{E}^{2}}+B{{E}^{2}}\]

\[=A{{D}^{2}}-D{{E}^{2}}+{{\left( \frac{1}{2}BC \right)}^{2}}\] [From (ii) and (iii)]

\[=A{{D}^{2}}-{{(BE-BD)}^{2}}+\frac{1}{4}B{{C}^{2}}\]

\[=A{{D}^{2}}-B{{E}^{2}}-B{{D}^{2}}+2.BE.BD+\frac{1}{4}B{{C}^{2}}\]

\[=A{{D}^{2}}-{{\left( \frac{1}{2}BC \right)}^{2}}-{{\left( \frac{1}{3}BC \right)}^{2}}\]\[+2.\frac{1}{2}BC.\frac{1}{3}BC+\frac{1}{4}B{{C}^{2}}\]

\[A{{B}^{2}}=A{{D}^{2}}-\frac{1}{9}B{{C}^{2}}+\frac{1}{3}B{{C}^{2}}\]

\[\Rightarrow \]   \[A{{B}^{2}}=A{{D}^{2}}+\frac{2}{9}B{{C}^{2}}\]

\[\Rightarrow \]   \[A{{B}^{2}}=A{{D}^{2}}+\frac{2}{9}A{{B}^{2}}\]          (\[\because \] \[BC=AB\])

\[\Rightarrow \]   \[A{{B}^{2}}-\frac{2}{9}A{{B}^{2}}=A{{D}^{2}}\]

\[\Rightarrow \]   \[\frac{7}{9}A{{B}^{2}}=A{{D}^{2}}\]

\[\Rightarrow \]   \[7A{{B}^{2}}=9A{{D}^{2}}\]

Or         \[9{{(AD)}^{2}}=7{{(AB)}^{2}}\]                              Hence Proved.

OR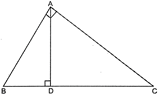

Given: \[\Delta \text{ }ABC\]is a right angle triangle, right angled at A.

To prove:         \[B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}\]

Construction: Draw \[AD\bot BC\].

Proof: In \[\Delta \text{ }ADB\]and \[\Delta \,BAC\],

\[\angle B=\angle B\]                        (Common)

\[\angle ADB=\angle BAC\]                          (Each \[90{}^\circ \])

\[\therefore \]      \[\Delta \text{ }ADB\tilde{\ }\Delta \text{ }BAC\]

(By AA similarity axiom)

\[\therefore \]      \[\frac{AB}{BC}=\frac{BD}{AB}\]                                                         (CPCT)

\[A{{B}^{2}}=BC\times BD\]                                                   ?(i)

Similarly,

\[\Delta \text{ }ADC\tilde{\ }\Delta \text{ }CAB\]

\[\frac{AC}{BC}=\frac{DC}{AC}\]

\[A{{C}^{2}}=BC\times DC\]                           ?(ii)

On adding eq. (i) and (ii)

\[A{{B}^{2}}+A{{C}^{2}}=BC\times BD+BC\times CD\]

\[=BC\text{ (}BD+CD)\]

\[=BC\times BC\]

\[A{{B}^{2}}+A{{C}^{2}}=B{{C}^{2}}\]

\[\Rightarrow \]   \[B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}\]                                       Hence Proved.