question_answer

As observed from the top of a 100 m high light house from the sea-level, the angles of depression of two ships are \[30{}^\circ \] and\[45{}^\circ \]. If one ship is exactly behind the other on the same side of the light house, find the distance between the two ships. [Use\[\sqrt{3}=1.732\]]

Answer:

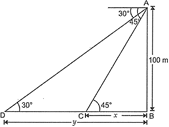
Let AB be the light house and two ships be at C and D.

In \[\Delta \text{ }ABC\],

\[\frac{BC}{AB}=\cot \,45{}^\circ \]

\[\Rightarrow \]               \[\frac{x}{100}=1\]

\[\Rightarrow \]               \[x=100\]                                              ...(i)

Similarly, in \[\Delta \text{ }ABD\],

\[\frac{BD}{AB}=\cot \,\,30{}^\circ \]

\[\Rightarrow \]               \[\frac{y}{100}=\sqrt{3}\]

\[\Rightarrow \]               \[y=100\sqrt{3}\]                                               ?(ii)

Distance between two ships \[=y-x\]

\[=100\sqrt{3}-100\]

[from (i) and (ii)]

\[=100\left( \sqrt{3}-1 \right)\]

\[=100(1.732-1)\]

\[=73.2\,\,m\]