Multiplication
Category : 4th Class
LEARNING OBJECTIVES
This lesson will help you to:-
Real Life Examples
Multiplication is used in daily household activities.
For example, if 2 glasses of water is required to cook 1 glass of rice. Then how many glasses of water are required to cook 5 glasses of rice.
72 people can sit in one train compartment. How many people are there on a train with 15 such compartments?
QUICK CONCEPT REVIEW
MULTIPLICATION
A hen laid 28 eggs & the chicks were born. She wants to distribute sweets to her friends & relatives. They have 20 families of friends & relatives.

She wants to give 6 sweets to each family. She started counting the number of sweets to be purchased from the market. 
She finds it quite difficult and time consuming to count the total number of sweets to be purchased. Can you help her find out an easier way to do so?
6 sweets are to be distributed to each family and there are 20 families in all. So instead of adding 6 again and again 20 times, we can simply multiply 6 by 20. The answer will be the same in both the cases.
6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 +
6 + 6 + 6 + 6 = \[6\times 20=120\] sweets.
Therefore, we can say that multiplication is a short form of repeated addition.
It is a mathematical operation that indicates how many times a number is added to itself.
Multiplication is the process of finding the product of any two numbers.
TERMINOLOGY
When multiplication is considered as repeated addition:
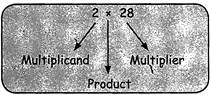
The, number to be multiplied is called the multiplicand. The number of multiples is called the multiplier. When any two numbers are multiplied: The numbers to be multiplied are called factors or multiplicands.

The result after multiplication is known as the product.
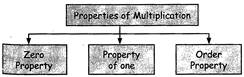
PROPERTIES OF MULTIPLICATION
Amazing Facts
Multiplying two same numbers with 5 at ones place.
Example, \[45\times 45=?\]
The last two digits of the answers will always be 25.
Now multiply 4 by the number that follows it i.e.
\[5.\left( 4\times 5=20 \right)\]
Write the number in front of 25. \[\underline{2025}\]
Therefore, \[45\times 45=2025\]
Multiplying by 11.
For multiplying any number by 11, just place the first and last digit as it is on their respective places and add the two digits and place the sum between the first and last digit.
Example,
Th H T O
\[11\times 11=\] 1 (1+1) 1
= 121
\[25\times 11=\] 2 (2+5) 5
= 275
\[124\times 11=\] 1 (1+2) (2+4) 4
= 1364
Did you know that
Methods of multiplication were documented in the Egyptian, Greek, Indian and Chinese civilizations.
If you can multiply\[9\times 3\],
Say it with me.
27
If you can multiply\[6\times 8\],
You are great.
48
We will multiply\[3\times 7\],
Look up the floor.
21
If you can multiply\[3\times 4\],
Stomp the floor.
12
If you can multiply\[1\times 9\],
Would you be mine?
9
When you multiply\[4\times 1\],
Then you’re having fun.
4
If you can multiply\[10\times 10\],…
If you can multiply\[7\times 2\],…
You multiply\[3\times 6\],…
If you can multiply\[6\times 5\],…
If you can multiply\[8\times 3\],…
Multiply\[10\times 4\],…
If you can multiply\[7\times 1\],…
If you can multiply\[5\times 10\],…
When you answer\[6\times 4\],…
There are no more!
ZERO PROPERTY
When we multiply any number by 0, the answer is always 0.
For Example: \[32\times 0=0\]
PROPERTY OF ONE
When we multiply any number by 1, the product is the number itself.
For Example: \[32\times 1=32\]
ORDER PROPERTIES
When two numbers are multiplied together, the product the same regardless of the order of the multiplicands. For example: \[4\times 2=2\times 4\]
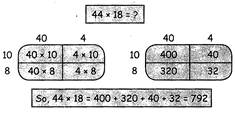
BOX MULTIPLICATION
In Box multiplication method we break the two numbers to be multiplied in ones, tens & hundreds.
For Example: if we want to multiply 44 by 18, we will break 44 & 18.
44 becomes 40 tens & 4 ones and 18 becomes 10 tens & 8 ones. Now we can multiply the numbers easily & quickly as shown below:
MULTIPLICATION BY 10’s & 100’s
If we want to multiply any number by 10, we will just write 0 in ones place & then multiply the number by 1.
For Example:
| Th | H | T | O | |
| \[2\times 10=\] | 2 | 0 | ||
| \[32\times 10=\] | 3 | 2 | 0 | |
| \[432\times 10=\] | 4 | 3 | 2 | 0 |
Therefore, to multiply by 10, we write 0 at ones place & multiply the rest numbers.
If we want to multiply any number by 100, we move the digits two places to the left & write two zeros at the end.
For Example:
| Th | H | T | O | |
| \[5\times 100~=\] | 5 | 0 | 0 | |
| \[26\times 100=\] | 2 | 6 | 0 | 0 |
MULTIPLYING BY A TWO DIGIT NUMBER

Kitty wants to knit pullovers, if it takes 24 wool balls to make 1 pullover, how many wool balls are required to make 52 pullovers.
To find out the no. of wool balls required we will multiply the no. of pullovers to be made & the no. of balls required to make 1 pullover.
\[52\times 24=?\]
Step 1:
Multiply by ones.
(52 x 4)
5 2
x 2 4
______
2 0 8 (52 x 4)
Step 2:
Multiply by tens.
(52 x 20)
5 2
x 2 4
_________
2 0 8 (52 x 4)
1 0 4 0 (52 x 20)
Step 3:
Add the products.
(52 x 20)
5 2
x 2 4
_________
2 0 8 (52 x 4)
1 0 4 0 (52 x 20)
________
1 2 4 8
MULTIPLYING BY A THREE DIGIT NUMBER
The process of multiplying a number by a three digit number is the same as multiplying by a two digit number as explained above.
\[15873\times 7\times 2=222222\]
\[15873\times 7\times 3=333333\]and so on…
\[37\times 3\times 2=222\]
\[37\times 3\times 3=333\]and so on…
\[9\times 0+2=2\]
\[9\times 0+3=3\]
You need to login to perform this action.
You will be redirected in
3 sec
