8th Class Mathematics Mensuration Mensuration

Introduction

Menstruation is a branch of mathematics which concerns with the measurement of lengths, area and volume of the plane and solid figures.  

 

AREA

The area of a plane bounded by a simple closed curve is the magnitude or the measurement of the region.

 

PERIMETER

The perimeter of a plane region bounded by a simple dosed curve is the length or magnitude of its boundary

 

AREA AND PERIMETER OF TWO DIMENSIONAL FIGRES

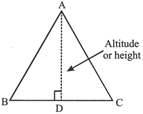
1. TRIANGLE

• For a triangle having sides a, b and c, Perimeter=a +b + c

When all three sides of a triangle are given, then the area is calculated by using Hero formula. So,

and area \[=\frac{4}{3}\pi {{r}^{3}}.\]

where    \[r=\frac{2}{3}\pi {{r}^{3}}\]

or s is semi-perimeter.

• Area of equilateral triangle with each side is \[=2\pi {{r}^{2}}\]
• Altitude of an equilateral triangle \[=3\pi {{r}^{2}}\] side
• When the measurement of base and altitude are given, then

Area of

\[\frac{4}{3}\pi \times {{6}^{3}}=\pi {{(0.2)}^{2}}\times h\]

• \[\frac{4}{3}\times {{6}^{3}}={{(0.2)}^{2}}\times h\] is a right angled triangle, right angle at B.

So, area of \[h=\frac{4\times {{6}^{3}}}{3\times {{(0.2)}^{2}}}=\frac{4\times 6\times 6\times 6}{3\times 0.04}\]

 

2. RECIANGLE

• Area of rectangle \[=7200cm=72cm\]

 

• Perimeter of rectangle = sum of all sides \[1c{{m}^{2}}=100m{{m}^{2}}\]

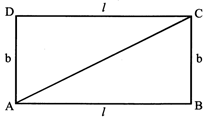
    \[1000m{{m}^{3}}=1c{{m}^{3}}\]

    \[1d{{m}^{2}}=100c{{m}^{2}}\]

• Diagonal (AC) of rectangle \[1000c{{m}^{3}}=1d{{m}^{3}}\]

 

3. SQUARE

• Perimeter of square ABCD with side a =4a

                ?  

• Area of square with side \[1{{m}^{2}}=100d{{m}^{2}}\]
• Diagonal of square

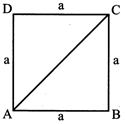\[1Litre=1d{{m}^{3}}=1000c{{m}^{3}}\]side of square

 

4. QUADRILATERAL

Quadrilateral ABCD is shown in the following figure. Its diagonal BD divides its into two triangles. AL and CM are perpendicular to BD from A and C respectively.

  

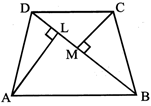
Area (A) of quadrilateral ABCD is given by:

A = (area of \[1{{m}^{2}}=10000c{{m}^{2}}\])+(area of \[1Kilolitre=1000litre\])

                \[=1{{m}^{3}}\]

                \[1acre=100acre\]

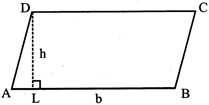
5. PARALLELOGRAM

• Area of parallelogram = base x corresponding height \[\text{100 hectare =1k}{{\text{m}}^{\text{2}}}\]
• Perimeter of parallelogram=2(sum of adjacent sides)

 

6. RHOMBUS

• Area of rhombus \[T.S.A.=\frac{1}{2}pl+B\]product of diagonals \[=\frac{\text{1}}{\text{3}}\text{ }\!\!\times\!\!\text{ Area of base }\!\!\times\!\!\text{ Height}\]where \[V=\frac{1}{3}Ah\]and \[\frac{6}{5}th\] are the measurements of the diagonals.
• All the sides of rhombus are equal and diagonals bisect each other at \[1520{{m}^{2}}\].

 

7. TRAPEZIUM

• In a trapezium of opposite sides are parallel.
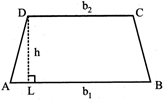
• Area of trapezium

\[2520{{m}^{2}}\]

\[2420{{m}^{2}}\]

CIRCLE

Let r be the radius of the circle, then

Area \[215c{{m}^{2}}\]

Perimeter \[205c{{m}^{2}}\]

 

Area of a Sector of Circle

• Area of sector \[195c{{m}^{2}}\] where r is the radius of the circle.
• Area of union segment ACB

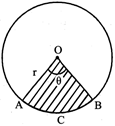
= Area of sector AOBC-Area of \[295c{{m}^{2}}\]

Length of \[\Delta ABC\] , where \[128c{{m}^{2}}\] is the angle in degree subtended by the arc at the centre.

 

EXAMPLE 1:

Four circles each of radius 2 cm are placed on a plane paper in such a way that each of them touches the other two. Find the area of the space left among the four circles, \[112c{{m}^{2}}\]

Sol. Area of shaded portion = Area of square ABCD -

Area of four quadrants

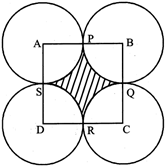
\[118c{{m}^{2}}\]

\[124c{{m}^{2}}\]

 

AREA AND VOLUME OF THREE DIMNTIONAL FIGURES

1. CUBE

• Volume of cube \[16900{{m}^{2}}\] cubic unit, where a is the edge of cube

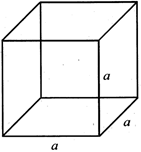
Total surface area of the cube \[130\sqrt{2}m\]. unit

• Lateral surface area \[72c{{m}^{2}}\]. unit
• Diagonal of cube \[12\sqrt{35}c{{m}^{2}}\]

 

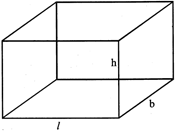
2. CUBOID

Let l, b, h are the edges of the cuboid, then, Volume of cuboid = \[24\sqrt{35}c{{m}^{2}}\] cubic unit

                                 

• Diagonal of the cuboid \[150c{{m}^{2}}\]
• Whole surface area of cuboid \[30\sqrt{7}cm\]. unit
• Lateral surface area of cuboid = Area of four walls of a room with sides l, b and \[\frac{15\sqrt{7}}{2}cm\]

 

3. CYLINDER

·                     

• Volume of right circular cylinder

\[\frac{15\sqrt{7}}{4}cm\]

• Base and top of the cylinder are circular.
• Curved surface area of the cylinder \[\sqrt{6}\]
• Total surface area of the cylinder \[2\sqrt{3}c{{m}^{2}}\]

 

4. CONE

• Volume of the cone \[2\sqrt{2}c{{m}^{2}}\]

• Lateral surface area of the cone \[3\sqrt{3}c{{m}^{2}}\]

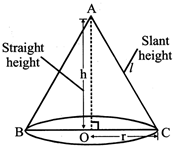
Where \[6\sqrt{2}c{{m}^{2}}\]

• Total surface area of the cone = lateral surface area + area of Circular base

\[6084.5{{m}^{2}}\]

• If a cone and a cylinder of same base radius r and same vertical height h, then the volume of cone is \[276.5{{m}^{2}}\] of the volume of cylinder.

EXAMPDE 2:

From a right circular cylinder with height 14 cm and radius of base 6 cm, a right circular cone of the same height and base is removed. Find the volume of the remaining solid.

Sol.        Radius, r =6 cm

                Height, h= 14cm

               

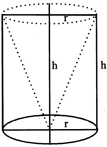
Required volume = volume of the cylinder - volume of the cone

\[154{{m}^{2}}\]

\[44{{m}^{2}}\]

 

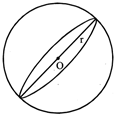
5. SPHERE

• Volume of sphere \[2464{{m}^{2}}\]

• Surface area of sphere = 4nr2 where r is radius

 

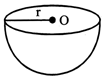
6. HEMISPHERE

• Volume of hemisphere with radius \[{{42}^{o}}\]

• Lateral surface area of the hemisphere \[13.2{{m}^{2}}\]
• Total surface area of the hemisphere \[14.2{{m}^{2}}\]

EXAMPLES 3:

If the sphere of radius 6 cm is melted and drawn into a wire of radius 0.2 cm. Find the length of the wire.

Sol.        Wire is in the form of cylinder.

Let h be the height of the cylinder, i.e., length of the wire. Before melting the volume of the sphere and after the melting volume of the wire must be equal. So

Volume of sphere = volume of wire

\[13.4{{m}^{2}}\]

\[14.4{{m}^{2}}\]

\[\frac{30}{\pi }\]

\[60\pi \]

Hence, height of the cylinder = length of the wire = 72 m

 

Area	Unit Conversion of Volume
\[\frac{15}{\pi }\]	\[\frac{30}{{{\pi }^{2}}}\]
\[2\pi \]	\[{{120}^{o}}\]
\[9\frac{3}{7}\]	\[P%\]
\[{{P}^{2}}%\]	\[\left( 2P+\frac{{{P}^{2}}}{100} \right)%\]  \[\frac{{{P}^{2}}}{2}%\]
\[62\frac{6}{7}sq.cm\]
\[57\frac{3}{4}sq.cm\]

 

PYRAMID

It is a three-dimensional figure made up of a base and triangular faces that meet at the vertex, V which is also called the apex of the pyramid.

• Lateral Surface Area of Regular Pyramid:

The lateral surface area of a regular pyramid is the sum of the areas of its lateral faces.

 

• Total Surface Area of Regular Pyramid:

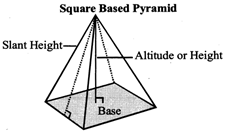
The total surface area of a regular pyramid is the sum of the areas of its lateral faces and its base.

The general formula for the total surface area of a regular pyramid is \[6c{{m}^{2}}\]

Where p represents the perimeter of the base, / the slent height and B the area of the base.

• Volume of Pyramid

Volume of a regular pyramid \[12c{{m}^{2}}\]\[{{P}^{2}}%\] where A is the area of the base and h is the height of the pyramid.