8th Class Mathematics Related to Competitive Exam Series

Series

Category : 8th Class

Introduction

In a Series a number of objects or arranged or coming one other in succession. Series is simply adding the terms in a sequence. An arithmetic series involves adding the terms of an arithmetic sequence and a geometric series involves adding the terms of a geometric sequence.

NUMBER SERIES

In this type of series, the set of given numbers in a series are related to one another in a particular pattern or manner. The relationship between the numbers maybe

(i) consecutive odd/even numbers,

(ii) Consecutive prime numbers,

(iii) Squares/cubes of some numbers with/without variation of addition or subtraction of some number,

(iv) Sum/product/difference of preceding number(s),

(v) Addition/subtraction/multiplication/division by some number, and

(vi) Many more combinations of the relationships given above.

EXAMPLE 1:

Find the missing term in the following sequence.

5,11,24,51,106.......................

Sol. Double the number and then add to it

1,2,3,4 etc.

Thus the next term is \[2\times 106+5=217.\]

EXAMPLE 2:

Complete the series 4, 9, 16, 25...........

(a) 32 (b) 42

Sol. (d) Each number is a whole square.

EXAMPLES 3:

Find the wrong term in the series 3, 8, 15, 24,34,48,63.

(a) 15 (b) 12

Sol. (c) \[8-3=5\]

\[15-8=7\]

\[24-15=9\]

\[34-24=10\]

\[48-34=14\]

\[63-48=15\]

Obviously difference should be 11 & 13 instead of 10 & 14. Therefore, 34 is the wrong term.

EXAMPLES 4:

Complete the given series 4, 9,13,22,35..........

(a) 57 (b) 70

Sol. (a) \[4+9=13, 13+9=22\] etc.

EXAMPLES 5:

Complete the given series 66, 36, 18...........

(a) 9 (b) 3

Sol. (d) \[6\times 6=36;3\times 6=18;1\times 8=8.\]

EXAMPLE 6:

Complete the given series 61, 67,71,73,79,...

(a) 81 (b) 82

Sol. (c) Prime number series. 83 is the next prime number.

EXAMPLE 7:

Complete the given series 8, 24, 12,36,18,54,

(a) 27 (b) 29

Sol. (I) Multiply by 3 and divide the result by 2.

Next term is \[\frac{54}{2}=27\]

ALPHABET SERIES

In this type of question, a series of single, pairs or groups of letters or combinations of letters and numbers is given. The terms of the series form a certain pattern as regards the position of the letters in the English alphabet.

In the following questions, various terms of a letter series are given with one term missing as shown. Choose the missing term out of the options.

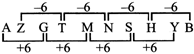
EXAMPLES 8:

AZ, GT.MN,...........,YB

(a) KF (b) RX

Sol. (c) The logic is+6 and-6.

EXAMPLE 9:

Choose the missing term from the given options.

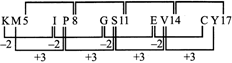
KM5, 1P8, GS11, EV14,

(a) BX17 (b) BY17

Sol. (d) Logic for the letters is -2, +3 steps, numbers added is 3.

DIRECTIONS (Example 10 – 12): In each of the following questions, various terms of an alphabet series are given with one or more terms missing as shown by ‘?’. Choose the missing terms out of the given alternatives.

EXAMPLE 10:

U, B, I, P, W, ?

(a) D (b) F

Sol. (a) \[U\xrightarrow{+7}B\xrightarrow{+7}I\xrightarrow{+7}B\xrightarrow{+7}W\xrightarrow{+7}(D)\]

EXAMPLE 11:

A,B,B,D,C,F,D,H,E,?,?

(a) E, F (b) F, G

Sol. (d) The given sequence is a combination of two series:

lst,3rd,5th,7th,9th,llthtermsi.e.A,B,C,D,E?

II.2nd, 4th, 6th, 8th, 10th terms i.e. B, D, F, H?

Clearly, I consists of consecutive letters while II consists of alternate letters. So, the missing letter in I is F, while that in II is J.

So, the missing terms i.e. 10th and 11th terms are J and F respectively.

EXAMPLE 12:

UPI, ?, ODP, MBQ, IAW

(a) RHJ (b) SHJ

Sol. (b)

1st letter:

\[U\xrightarrow{-2}(S)\xrightarrow{-4}O\xrightarrow{-2}M\xrightarrow{-4}I\]

2nd letter:

\[P\xrightarrow{-8}(H)\xrightarrow{-4}D\xrightarrow{-2}B\xrightarrow{-1}A\]

3rd letter:

\[I\xrightarrow{+1}(H)\xrightarrow{+6}D\xrightarrow{+1}B\xrightarrow{+6}W\]

CONTINUOUS PATTERN SERIES:

This type of question usually consists of a series of small letters which follow a certain pattern. However, some letters are missing from the series. These missing letters are then given in a proper sequence as one of the alternatives.

DIRECTIONS (Example 13 -17): In each of the following letters series, some of the letters are missing which are given in that order as one of the alternatives below it. Choose the correct alterative.

EXAMPLE 13:

a......... bcc.........ac...........aabb.......... ab……..cc

(a) aabca (b) abaca

Sol. (c) The series is \[\underline{b}\]b c c \[\underline{a}\] a/c \[\underline{c}\] a a b b/ \[\underline{a}\]a b \[\underline{b}\]cc.

The letter pairs move in a cyclic order.______

EXAMPLE 14:

a........bccb......ca........ cca........... baab........... c

(a) ababc (b) abcaa

Sol. (a) The series is a a b c c/ b b c a a / c c a b b/ a a b c c.

The letters move in a cyclic order and in each group, the first and third letters occur twice.

EXAMPLE 15:

ab........aa.........caab.........c........... abb........... c

(a) bbcaa (b) bcbca

Sol. (d) The series is a b c /a a b c/a a b b c/a a b b c c.

First all the letters occur once, then a occurs twice, then both a and b occur twice and finally all the three letters appear twice.

EXAMPLE 16:

c.......baa.........ca..........acab........acac........bca

(a) acbaa (b) bbcaa

Sol. (a) The series is

c a b/a a/c a c a b/c a c a b/a a/c a c a b/c a.

Thus, the pattern cacab, cacab, aa is repeated.

EXAMPLE 17:

bca - b - aabc - a - caa

(a) acab (b) bcbb

Sol. (a) The series is bcaa/bcaa/bcaa/bcaa.

Thus, the pattern 'bcaa' is repeated.

ALPHA – NUMBER SERIES:

A series in which both alphabets and numbers are used is called Alpha numeric.

DIRECTION (Example 18-20): In each of the following questions a letter number series is given with one or more terms missing as shown by (?), chose the missing term out of the given alternatives.

EXAMPLE 18:

D-4,F-6,H-8,J-10,??

(a) K-12.M-13 (b) L-12.M-14

Sol. (c) The letters in the series are alternate and the numbers indicate their position in the English alphabet from the beginning.

EXAMPLE 19:

'2A11, 4D13, 12G17,?

(a) 36119 (b) 36J21

Sol. (d) 1st number:

\[2\xrightarrow{\times 2}4\xrightarrow{\times 3}12\xrightarrow{\times 4}(48)\]

Middle letter:

\[A\xrightarrow{+3}D\xrightarrow{+3}G\xrightarrow{+3}(J)\]

3rd number:

\[11\xrightarrow{+2}13\xrightarrow{+4}17\xrightarrow{+6}(23)\]

EXAMPLE 20:

Find the missing term.

2Z5, 7Y7, 14X9, 23 W 11,34V 13,?

Sol. First number is the sum of the numbers of the

preceding term.

Middle letter is moved one step backward.

Third number is a series of odd numbers.

\[\therefore \] 6th term = 47 U 15.

Miscellaneous Solved Examples

Choose the missing term from the given options:

EXAMPLE 1:

1, 1 ,3, 9, 6, 36, 10, 100,…….225

(a) 15 (b) 16

Sol. (I) The given series is a mixture of two series:

1,3, 6, 10,....
1,9,36,100,125

The logic of I is \[+2,+3,+4,+5,\]and the logic of II is the squares of the corresponding numbers of I. So the missing number is 10 + 5 i.e. 15.

EXAMPLE 2:

Complete the series': 0,2,3,5,8,10,15,17,24,26,……

(a) 35 (b) 32

Sol. (I) Sequence given is a combination of two series:

0, 3, 8, 15, 24,....... and II. 2,5,10,17,26.

The pattern in both the series is \[+3,+5,+7,+9\] etc.

DIRECTIONS (Example 3 - 4): In each of the following questions, one term is wrong. Find out the wrong term.

EXAMPLE 3:

1,2,4,8,16,32, 64,96

(a) 4 (b) 32

Sol. (d) Each term is double the preceding term, so 96 is the wrong term. It should be 128.

EXAMPLE 4:

1,5,5,9,7,11,15,12,17

(a) 11 (b) 12

Sol. (b) The given sequence is a combination of two series

1.1,5,7,11,12 And II. 5, 9,11,15,17

The pattern is both I and II is \[+4,+2,+4,+2,\] So 12 is wrong and must be replaced by \[11+2\] i.e. 13.

DIRECTIONS (Example 5 -11): In each of the follow2ing questions, a sequence of groups of letters and numbers is given with one term missing as shown by (?). Choose the missing term out of the given alternatives.

EXAMPLES 5:

What will be next term in BDF, CPI, DHL,?

(a) CJM (b) HM

Sol. (c) Clearly first, second, third letters of each term are respectively moved one, two and three steps forward to obtain the corresponding letters of the next term

EXAMPLES 6:

KM5, IP8, GS11,' EV14,?~

(a) BX17 (b) BY17

Sol. (d) The first letter of each term is moved two steps backward and the second letter is moved three steps forward to obtain the corresponding letters of the next term. The number in each term is 3 more than that in the preceding term.

EXAMPLES 7:

X O I F?

(a) D (b) F

Sol. (b) The series following the sequence of the difference decreasing by 3 i. e.

EXAMPLES 8:

B D A C F H E G?

(a) JL (b) IK

Sol. (a) The letters in the series are arranged in following order (Four letters are mixed)

is written as BDAC; and

as FHEG Similarly,

will be JLIK.

The answer option is JL i.e., A

EXAMPLES 9:

2,7,12,17,22,27..............

Sol. Here the difference between the two successive terms is the same i.e. 5.

The next number is therefore \[27+5=32.\].

EXAMPLES 10:

23, 35,57,711,1113...

Sol. This is a series obtained from. the prime numbers taken in pairs, so the next term is 1317.

EXAMPLES 11:

12, 25, 53, 111, 229,....

Sol. The number follow the rule

\[\times 2+1,\times 2+3,\times 2+5,\times 2+5,\times 2+7\]etc. The next number is \[229\times 2+9=467.\]

DIRECTION (Example 12 – 19): In the following first examples there is a letter series in the first row and a number series in the second row. Each number in the number series stand for a letter. Since in each of that series some terms are missing, you have to find out as to what those terms are and answer the questions based on these as given below the series.

EXAMPLES 12:

The last four terms in the series are

(a) 1222 (b) 2221

Sol. (c) Observe the options for the answer. We have only 1 and 2 in numbers and a, b in letters. It is easily seen that b is matched with 2 and so 'a9 should be matched with 1. We have a b in the beginning. It is again repeated after a few places. We have ab - bba. This strongly suggests that in the first blank, we have 'a, With a careful observation we see that the pattern is

a b a b b a b b b a b b b b a b

1 2 1 2 2 1 2 2 2 1 2 2 2 2 1 2

Hence the last four terms in the series are 2 2 1 2.

EXAMPLES 13:

a c b - - d e b c a - c – e d d - - -

-2 – 35- - - - -4 - -1- - - -

The last five terms in the number series are

(a) 53214 (b) 35124

Sol. (c) We have five letters a c b e d which are reversed in the second round as 'd e b c a' and so on we therefore have

\[a\to 4,c\to 2,e\to 3,d\to 5\] and the remaining \[b\to 1.\]

EXAMPLES 14:

ab- --bc-- - -c-e-d - - - -

-3- - - - -5-7- -99 - 7

The last four terms in the letter series are

(a) c d e e (b) c d f e

Sol. (c) We notice b 's again separated by two spaces. Between c 's we have 'd' and between d 's we have T. Hence the series should be a, b c c b, c d d c, d e e d. e.

EXAMPLES 15:

-b x p m – x g m p - - b p - - - -

2 – 3 – 5 1 - - - - 4 - - - - - - - - -

The last five terms in the number series are

(a) m b g p x (b) m g b p x

Sol. (a) Compare to arrive at the following correspondence \[x\to 3,\]\[m\to 5,\]\[p\to 4.\] Remaining letters b and g should correspond to 2 and 1 or 1 and 2 respectively The first place is to be filled by g, hence it is most probable that \[g\to 2\] and \[b\to 1.\].

Hence the number series is

2	1	3	4	5
1	3	2	4	4
-	-	1	4	-
-	-	-	-	-

2,1, 3 is changed to 1,3,2, then it should be changed to 3,2, 1 and finally as 2.1-3

EXAMPLES 16:

What number should replace the question mark?

7	4	5	3
1	6	3	7
3	8	1	7
6	1	8	?

Sol. (b) Each alternate row and column sums to 19 and 17.

EXAMPLES 17:

6,50,402,3218?

What number comes next in the above sequence?

Sol. 25746

Multiply the previous number by 8 and add 2 each time

EXAMPLES 18:

1, 2, 9, 4, 25, 6, ……..

(a) 8 (b) 27

Sol. (d) In fact, this is the combination of two series viz., g

12,32,52,72,............. and2,4,6,.......... The numbers of the two series are placed alternately.

EXAMPLES 19:

GMSY, IOUA, KQWS,?

(a) MSYE (b) NSYE

Sol. (a) The series is formed by moving each letter two steps forward from one group to the next.

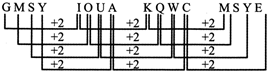
(The series restarts from A on reach in a Z)

Number and Ranking

8th Class Mathematics Related to Competitive Exam Series

Other Topics