Slope of the Tangent and Normal
Category : JEE Main & Advanced
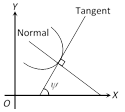
(1) Slope of the tangent : If a tangent is drawn to the curve \[y=f(x)\] at a point \[P({{x}_{1}},\,{{y}_{1}})\] and this tangent makes an angle \[\psi \] with positive x-direction then, \[{{\left( \frac{dy}{dx} \right)}_{({{x}_{1}},\,{{y}_{1}})}}=\tan \psi =\] Slope of the tangent.
· If the tangent is parallel to x-axis, \[\psi =0\Rightarrow {{\left( \frac{dy}{dx} \right)}_{({{x}_{1}},\,{{y}_{1}})}}=0\]
· If the tangent is perpendicular to x-axis, \[\psi =\frac{\pi }{2}\Rightarrow {{\left( \frac{dy}{dx} \right)}_{({{x}_{1}},\,{{y}_{1}})}}\to \,\,\,\infty \]
(2) Slope of the normal : The normal to a curve at a point \[P({{x}_{1}},\,{{y}_{1}})\] is a line perpendicular to the tangent at P and passing through P. Slope of the normal \[=\frac{-1}{\text{Slope of tangent }}=\frac{-1}{{{\left( \frac{dy}{dx} \right)}_{P({{x}_{1}},\,{{y}_{1}})}}}=-{{\left( \frac{dx}{dy} \right)}_{P({{x}_{1}},\,{{y}_{1}})}}\].
· If the normal is parallel to x-axis, \[-{{\left( \frac{dx}{dy} \right)}_{({{x}_{1}},\,{{y}_{1}})}}=0\] or \[\frac{b}{a}=\frac{c}{b}\].
· If the normal is perpendicular to x-axis (or parallel to y-axis), \[-{{\left( \frac{dy}{dx} \right)}_{({{x}_{1}},\,{{y}_{1}})}}=0\].
You need to login to perform this action.
You will be redirected in
3 sec
