JEE Main & Advanced Mathematics Functions Domain, Co-domain and Range of Function

If a function \[f\] is defined from a set \[f\] to set B then for \[f:A\to B\] set A is called the domain of function \[f\] and set \[B\] is called the co-domain of function \[f\]. The set of all f-images of the elements of \[A\] is called the range of function \[f\].

In other words, we can say 

Domain = All possible values of \[x\] for which \[f(x)\] exists.

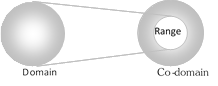
Range   = For all values of \[x,\] all possible values of \[f(x)\].

(1) Methods for finding domain and range of function

(i) Domain

(a) Expression under even root (i.e., square root, fourth root etc.) \[\ge 0\].  Denominator \[\ne 0\].

If domain of \[y=f(x)\] and \[y=g\,(x)\] are \[{{D}_{1}}\] and \[{{D}_{2}}\] respectively then the domain of \[f(x)\pm g\,(x)\] or \[f(x).g\,(x)\] is \[{{D}_{1}}\cap {{D}_{2}}.\]

While domain of \[\frac{f(x)}{g(x)}\] is \[{{D}_{1}}\cap {{D}_{2}}-\{g(x)=0\}.\]

Domain of \[\left( \sqrt{f(x)} \right)={{D}_{1}}\cap \{x:f(x)\ge 0\}\]

(ii) Range : Range of \[y=f(x)\] is collection of all outputs \[f(x)\] corresponding to each real number in the domain.

(a) If domain \[\in \] finite number of points \[\Rightarrow \] range \[\in \] set of corresponding \[f(x)\] values.

(b) If domain \[\in R\] or \[R-\] [some finite points]. Then express \[x\] in terms of \[y\]. From this find \[y\] for \[x\] to be defined (i.e., find the values of \[y\] for which \[x\] exists).

(c) If domain \[\in \] a finite interval, find the least and greatest value for range using monotonicity.