JEE Main & Advanced Mathematics Trigonometric Equations Ex-central Triangle

Let ABC be a triangle and I be the centre of incircle. Let \[{{I}_{1}}\], \[{{I}_{2}}\] and \[{{I}_{3}}\] be the centres of the escribed circles which are opposite to A, B, C respectively then \[{{I}_{1}}{{I}_{2}}{{I}_{3}}\] is called the Ex-central triangle of \[\Delta ABC\].

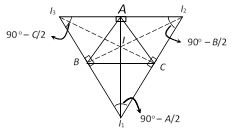
\[{{I}_{1}}{{I}_{2}}{{I}_{3}}\] is a triangle, thus the triangle ABC is the pedal triangle of its ex-central triangle \[{{I}_{1}}{{I}_{2}}{{I}_{3}}\]. The angles of ex-central triangle \[{{I}_{1}}{{I}_{2}}{{I}_{3}}\] are  \[{{90}^{o}}-\frac{A}{2},\,\,{{90}^{o}}-\frac{B}{2},\,\,{{90}^{o}}-\frac{C}{2}\] and sides are \[{{I}_{1}}{{I}_{3}}=4R\cos \frac{B}{2};\,\,{{I}_{1}}{{I}_{2}}=4R\cos \frac{C}{2};\,\,{{I}_{2}}{{I}_{3}}=4R\cos \frac{A}{2}\].

Area and circum-radius of the ex-central triangle 

Area of triangle

\[=\frac{1}{2}\] (Product of two sides) \[\times \] (sine of included angles)

\[\Delta =\frac{1}{2}\,\,\left( 4R\cos \frac{B}{2} \right)\,\,.\,\,\left( 4R\cos \frac{C}{2} \right)\times \sin \left( {{90}^{o}}-\frac{A}{2} \right)\]

\[\Delta =8{{R}^{2}}\cos \frac{A}{2}.\cos \frac{B}{2}.\cos \frac{C}{2}\]

Circum-radius \[=\frac{{{I}_{2}}{{I}_{3}}}{2\sin {{I}_{2}}{{I}_{1}}{{I}_{3}}}=\frac{4R\cos \frac{A}{2}}{2\sin \left( {{90}^{o}}-\frac{A}{2} \right)}=2R\].