question_answer 47)

                  A steel rod of length 2l, cross-sectional area A and mass M is set rotating in a horizontal plane about an axis passing through the centre. If Y is the Young?s modulus for steel, find the extension in the length of the rod. (Assume the rod in uniform).                

Answer:

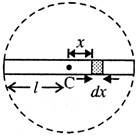
                  Let mass per unit length \[(m/l)\] of the rod be \[\mu \]. Consider a small element of length \[dx\] at a distance \[x\] drom at centre of the rod.                 Mass of the element, \[dm=(\mu \,dx)\]                 Centripetal force acting on the small element,                 \[dF=(dm){{\omega }^{2}}x=(\mu {{\omega }^{2}}x)\,dx\]                 The tension is the rod is the function of \[x\].                 The difference in the tension at two ends of the element provides the centripetal force.                 The difference in the tension \[=(T-dT)-T\]                 \[=-dT\]                 \[\therefore \] \[-\,dT\,=\,dF\]                 or \[-dT=\,(\mu {{\omega }^{2}})\,dx\]                 \[\therefore \] \[-\int_{{}}^{{}}{dT=\,\int\limits_{t}^{x}{\mu {{\omega }^{2}}x\,dx}}\]                 or \[-\,T\,(x)\,=\,\mu {{\omega }^{2}}\,\left( \frac{{{x}^{2}}}{2}-\,\frac{{{l}^{2}}}{2} \right)\,=\,\frac{\mu {{\omega }^{2}}}{2}({{x}^{2}}-{{l}^{2}})\]                 or \[T(x)\,=\,\frac{\mu {{\omega }^{2}}}{2}\,({{l}^{2}}-{{x}^{2}})\]                 If \[dy\] the extension of the small element of length dx, then from \[Y=\,\frac{{{T}_{(x)}}\,dx}{A\,dy},\] we get                 \[dy=\frac{T(x)\,dx}{\,YA}\]                 or \[dy\,=\,\frac{\mu {{\omega }^{2}}}{2YA}\,({{l}^{2}}-{{x}^{2}})\,dx\]             ?.. (i)                 Now, \[Y=\,2\,\times \,{{10}^{11}}\,N{{m}^{-2}},\]\[A=\,\pi {{r}^{2}}=3.14\times {{10}^{-6}}\,{{m}^{2}}\]                 m = Area × length × density                 \[=3.14\times {{10}^{-6}}\,\times 10\,\times \,7860\,\,=\,0.25\,\,kg\]                 \[M=25\,kg\]                 \[\therefore \] \[l=\,\frac{1}{2\times \,{{10}^{11}}\times 3.14\times \,{{10}^{-6}}}\]                 \[\left[ \frac{0.25\times \,10\times \,10}{2}+\,25\times \,10\times \,10 \right]\]                 \[=\,\frac{2512.5}{6.28\,\times \,{{10}^{5}}}=\,4.0\,\,\times \,{{10}^{-3}}\,m\] (b) Maximum tension in the wire                 \[=\,\mu gL\,+\,Mg\]                 \[=\,mg+\,Mg\,=\,(m+M)\,g\]                 Also force = Yield strength × Area of cross-ection.                 \[=\,2.5\,\times \,{{10}^{8}}\,\times \,\pi {{r}^{2}}\]                 \[=\,2.5\,\times \,{{10}^{8}}\,\times \,3.14\,\,\times \,{{10}^{-6}}\,=785\ N\]                 Now \[m=0.25\,\,kg\]                 \[\therefore \]\[(0.25\,\,+\,M)\,g=785\]                 or \[M=\,\frac{785}{10}-\,0.25\,\,=\,78.25\,\,kg\]                 Now, total extension in the rod.                 \[y=\,\int\limits_{-1}^{1}{\frac{\mu {{\omega }^{2}}}{2YA}\,\,({{l}^{2}}-{{x}^{2}})\,dx}\]                 \[=\,\frac{\mu {{\omega }^{2}}}{YA}\,\int\limits_{0}^{1}{({{t}^{2}}-{{x}^{2}})\,dx}\]                 \[=\,\frac{\mu {{\omega }^{2}}}{YA}\,\left[ {{l}^{3}}+\,\frac{{{l}^{3}}}{3} \right]\,=\,\frac{2\mu {{\omega }^{2}}}{3YA}\,{{l}^{3}}\]