Answer:
(a)
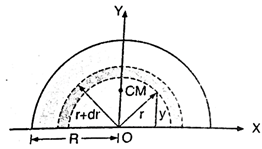If M is the mass of
the half-disc, of radius R, then mass per unit area of the half-disc,
\[\sigma
=\frac{M}{\pi {{R}^{2}}/2}=\frac{2M}{\pi {{R}^{2}}}\]
Let
us consider an element (which is a circular wire) of this disc between \[r\]
and \[(r+dr)\].
Area
of the element \[=\frac{1}{2}[\pi {{(r+dr)}^{2}}-\pi {{r}^{2}}]\]
\[=\frac{\pi
}{2}[{{r}^{2}}+{{(dr)}^{2}}+2rdr-{{r}^{2}}]\]
\[=\pi
rdr\]
Mass
of the element,
\[dm=(\pi
rdr)\sigma =(\pi rdr)\left( \frac{2M}{\pi {{R}^{2}}}
\right)=\frac{2Mr}{{{R}^{2}}}dr\]
(i)
\[{{x}_{CM}}=0\]
(ii)
\[{{y}_{CM}}=\frac{1}{M}\int_{{}}^{{}}{y}dm=\frac{1}{M}\int\limits_{0}^{R}{\left(
\frac{2r}{\pi } \right)}\left( \frac{2Mr}{{{R}^{2}}}dr \right)\]
[as
it can be shown that \[y=2r/\pi \]]
\[=\frac{4}{\pi
{{R}^{2}}}\int\limits_{0}^{R}{{{r}^{2}}}dr=\frac{4}{\pi {{R}^{2}}}\left(
\frac{{{R}^{3}}}{3} \right)=\frac{4R}{3\pi }\]
Thus,
the CM of the half-disc is \[(0,\,4R/3\pi )\].
Comment: We can use the
Theorem of Pappus-Guldinus* to find the CM of the semicircular disc. It
state that
\[V=2\pi
{{y}_{CM}}A\]
Where
\[V\] is the volume of a sphere (of radius R), \[2\pi {{y}_{CM}}\] is the
distance travelled by the Cm of the semicircle in one revolution about X-axis
and A is the area of the semicircle.
Thus,
\[\frac{4\pi }{3}{{R}^{3}}=2\pi ({{y}_{CM}})\,\left( \frac{1}{2}\pi {{R}^{2}}
\right)\]
or \[{{y}_{CM}}=\frac{3}{{{\pi
}^{2}}{{R}^{2}}}=\frac{4R}{3\pi }\]
(b)
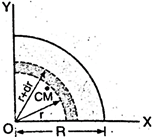For
quarter-disc
\[\sigma
=\frac{M}{\pi {{R}^{2}}/4}=\frac{4M}{\pi {{R}^{2}}},\]
area
of the element \[=\frac{1}{2}\pi rdr,\]
\[dm=\left(
\frac{1}{2}\pi rdr \right)\sigma =\frac{2Mr}{{{R}^{2}}}dr\]
\[{{x}_{CM}}=\frac{1}{M}\int_{{}}^{{}}{xdm}=\frac{1}{M}\int\limits_{0}^{R}{\left(
\frac{2r}{\pi } \right)}\left( \frac{2Mr}{{{R}^{2}}}dr \right)=\frac{4R}{3\pi
}\]
[as\[x=y=\frac{2r}{\pi
}\]]
Similarly,
\[{{y}_{CM}}=\frac{1}{M}\int_{{}}^{{}}{ydm}=\frac{4R}{3\pi }\]
Thus,
the CM of the quarter disc is \[\left( \frac{4R}{3\pi },\,\frac{4R}{3\pi }
\right)\].
You need to login to perform this action.
You will be redirected in
3 sec
