Answer:
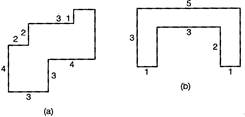
(a) Let the given figure be divided into rectangles A, B, C and D and their length and breadth be written on the figure. For rectangle A, Length = 4 cm and breadth = 2 cm Now, area of the rectangle A = Length \[\times \] Breadth \[=4cm\times 2cm=8sqcm\] For rectangle B, Length = 3 cm and breadth = 3 cm Area of the rectangle B = Length \[\times \] Breadth \[=3cm\times 3cm=9sqcm\] For rectangle C, Length = 2 cm and breadth = 1 cm Area of the rectangle C= Length \[\times \] Breadth = 2 cm \[\times \] 1 cm = 2 sq cm For rectangle D, Length = 3 cm and Breadth = 3 cm \[\therefore \]Area of the rectangle D = Length \[\times \] Breadth \[=3sqcm\times 3sqcm=9sqcm\] Now, total area of the given figure = Area of the rectangle A + Area of the rectangle B + Area of the rectangle C + Area of the rectangle D = (8 + 9 + 2 + 9) sq cm = 28 sq cm Hence, the required area is 28 sq cm. 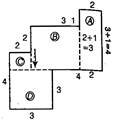 (b) Let the given figure is divided into rectangles A, B and C and their length and breadth are written on the figure. For rectangle A, Length = 2 cm and breadth = 1 cm \[\therefore \]Area of the rectangle A = Length \[\times \] Breadth \[=2\times 1=2sqcm\] For rectangle B, Length = 5 cm and breadth = 1 cm \[\therefore \]Area of the rectangle B = Length \[\times \] Breadth \[=5\times 1=5sq\,cm\] For rectangle C, Length = 2 cm and breadth = 1 cm Area of the rectangle C = Length \[\times \] Breadth \[=2\times 1=2sqcm\] Now, total area of the given figure = Area of rectangle A + Area of rectangle B + Area of rectangle C = (2 + 5 + 2) sq cm = 9 sq cm Hence, the area of the given figure is 9 sq cm.
(b) Let the given figure is divided into rectangles A, B and C and their length and breadth are written on the figure. For rectangle A, Length = 2 cm and breadth = 1 cm \[\therefore \]Area of the rectangle A = Length \[\times \] Breadth \[=2\times 1=2sqcm\] For rectangle B, Length = 5 cm and breadth = 1 cm \[\therefore \]Area of the rectangle B = Length \[\times \] Breadth \[=5\times 1=5sq\,cm\] For rectangle C, Length = 2 cm and breadth = 1 cm Area of the rectangle C = Length \[\times \] Breadth \[=2\times 1=2sqcm\] Now, total area of the given figure = Area of rectangle A + Area of rectangle B + Area of rectangle C = (2 + 5 + 2) sq cm = 9 sq cm Hence, the area of the given figure is 9 sq cm. 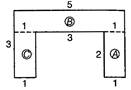
You need to login to perform this action.
You will be redirected in
3 sec
