Algebra
Category : 5th Class
Algebra
Learning Objectives
Introduction
We live in the world of numbers. We see them every day, on clocks, in sports, and all over the news. Algebra is all about figuring out the numbers we don't see. In this chapter, we will study about basic algebra and simple problems based on it.
Variables
Algebra is the branch of mathematics that uses letters in place of some unknown numbers we use numerals to represent numbers in arithmetic, in a similar way in Algebra, letters of the alphabet are used to represent numbers and these letters are called variables. Let us look at the puzzle of an unknown number.
\[?7=6\]
Here, we see, \[137=6\]
In algebra, we do not used blank boxes, we use a letter (say a, b, c, x, y, z, etc.). So, we can write it as: \[x7=6\]
Where, x is a variable or unknown number. Now, \[x7=6,\] or, \[\left( x7 \right)=6,\text{ }x0=7+6\] or \[x0=13\] . Or, \[x=13\] Clearly, here, \[x=13\] stands for the unknown number given in the box above.
We use letter for unknown number because, it is easier to write x than drawing empty boxes and also it is easier to say x than say empty box. If there are several empty boxes, or several unknown, we use different letters for different unknown.
Equation with One Variable
A linear equation in one variable has a single unknown quantity represented by a letter. The process of finding out the variable value that makes the equation true is called 'solving’ the equation. Clearly, an equation is a statement that two quantities are equivalent. For example, \[x+3=5\]means that when we added 3 to an unknown value ‘x’ the answer is equal to 5.
Solve for
Solution: Given equation is: \[x19=34\]
Now, add 19 to both side of the equation: \[\left( x19 \right)+19=34+19\]
Or, \[x+0=53,\] or \[x=53\]
Verification: \[x19=34,\] or \[5319=34\] .
Equation and Formula
We know that, perimeter of rectangle \[\text{=2}\!\!\times\!\!\text{ }\left(\text{length + breadth} \right)\text{=2 }\!\!\times\!\!\text{ }\left( \text{l + b} \right)\]
Then, variable 'l' stands for the length of rectangle and 'b' stands for the breadth of rectangle. Clearly, the letters ‘l’ and ‘b’ will represent different numbers for different rectangles.

Here, the letter 'C’ is used to denote the temperature in degrees in the Celsius scale and 'F' is used to denote the temperature in degrees in the Fahrenheit scale.
Simple Interest = \[\frac{\text{Prinidpal }\!\!\times\!\!\text{ Rate of Interest }\!\!\times\!\!\text{ Time}}{\text{100}}\]
Or, \[l.=\frac{P\times R\times T}{100}\]; Here, P, R and T stands for principal, rate of interest and time respectively.
Algebraic Expressions
As we know, an algebraic equation is a complete mathematical sentence that includes a sign of equality (or equal sign).
An algebraic expression is not a mathematical sentence. It is a mathematical phrase because it does not have an equal sign.
|
Algebraic Expression |
Algebraic Equation |
|
\[x+3\] or, \[7+3\] |
\[x+3=10\] or, \[7+3=10\] |
|
\[3x\] or \[3\times ~6\] |
\[3x=18\] Or, \[3\times ~6=18\] |
|
\[2\times ~\left( 1+7 \right)\] Or, \[2\left( x+7 \right)\] |
\[2\times ~\left( 1+7 \right)=16\] Or, \[2\times \left( x+7 \right)=16\] |
An expression is made up of terms, where these terms are separate values in an expression. They can be separated by operations, like plus and minus signs.
There are three parts of most expressions which are as follow:
Terms
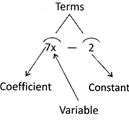
Variable: It is the unknown number x in the given expression above.
Coefficient: It is the number that is multiplied by the variable x. In the above expression, x is multiplied by 7, so 7 is the coefficient of x.
Constant: It is a fixed number that does not change. In the above expression, 2 is a constant.
For example, if \[x=12\] and \[y=4\], then \[xy=124=8\].
Where, x represents the number 12 and y represents the number 4.
For example, if \[x=7\] and \[y=4\] , then\[x\times ~y=xy=7\times ~4=28\].
Where, x represents 7 and y represents 4.
For example, if x = 27 and y = 3, then, \[x\div ~y=\frac{x}{y}=\frac{27}{3}=9\]
Where, x represents 27 and y represents 3.
For example, if x = 3 then \[{{x}^{2}}=\left( x \right)\times \left( x \right)=3\times 3=9\] and
\[{{x}^{3}}=\left( x \right)~\times \left( x \right)~\times \left( x \right)=3~\times 3\times ~3=27\].
(a) \[{{x}^{2}}+4y\]
(b) \[{{\left( x+4y \right)}^{2}}\]
(c) \[{{x}^{2}}+4{{y}^{2}}\]
(d) \[x+4{{y}^{2}}\]
(e) None of these
Answer: (a)
Explanation: Here, square of \['x'={{x}^{2}}\] and four times y = 4y
So, (square of ‘x’) plus (four times ‘Y’) \[={{x}^{2}}+4y\]
(a) Five times ‘Y’ minus two times ‘x’.
(b) Five times and two times of the difference of ‘x’ and ‘y’.
(c) Five times ‘x’ minus two times ‘y’.
(d) Two times ‘y’ minus five times ‘x’.
(e) None of these
Answer: (c)
Explanation: \[5x2y=5\times x2~\times y=\] Five times ‘x’ – Two times ‘y’.
So, \[5x2y\] means five times Y minus two times ‘y’.
Evaluating Expression
We can find the value of a given expression by substituting the value of the variable in the expression. Look at the following examples.
Solution: \[\frac{c-2a}{2b}=\frac{7-2\times 3}{2\times 4}=\frac{7-6}{8}=\frac{1}{8}.\]
Solution: \[5x{{y}^{2}}+xy3=(5\times x\times y\times y)+(x\times y3)\]
\[=(5\times ~7\times ~4\times ~4)+(7\times ~4\text{ =}3)=560+283=5883=585\].
(a) 19 (b) 17
(c) 23 (d) 27
(e) None of these
Answer: (c)
Explanation: Let be the other odd number is x.
Given that odd number = 17
Since, the sum of both odd numbers is 40.
Hence,\[x+17=40\], or \[\left( x+17 \right)17=4017\], or, \[x+0=23\], or, \[x=23\]
So, odd numbers are 23 and 17.
Commonly Asked Question
(a) \[15-\frac{x}{2}=20\]
(b) \[\frac{x}{2}-15=20\]
(c) \[20-\frac{x}{2}=15\]
(d) \[\frac{x}{2}-20=15\]
(e) None of these
Answer: (c)
Explanation: Given number = x Half of the number \[x=\frac{1}{2}x\]
Half of the number \[\times \] subtracted from \[20=20\frac{1}{2}x\]
So, half of a number (x) subtracted from 20 is 15 means \[20\frac{1}{2}x~=15\] or, \[20\frac{x}{2}~=15\]
(a) \[\frac{16}{21}\] (b) \[\frac{1}{8}\]
(c) \[\frac{11}{16}\] (d) \[\frac{16}{11}\]
(e) None of these
Answer: (c)
Explanation: \[\frac{{{a}^{2}}-b}{2c}=\frac{a\times a-b}{2\times c}=\frac{4\times 4-5}{2\times 8}=\frac{16-5}{16}=\frac{11}{16}\]
\[\frac{\mathbf{2x-5}}{\mathbf{3}}\mathbf{=4}\]
(a) \[\frac{17}{2}\] (b) \[\frac{15}{2}\]
(c) \[\frac{17}{3}\] (d) \[\frac{15}{3}\]
(e) None of these
Answer: (a)
Explanation: \[\frac{2x-5}{3}=4,\,\,or,\,\,\frac{2x-5}{{}}\times =4\times 3\]
Or, 2x – 5 = 12, or, (2x – 5) + 5 = 12 + 5
Or, 2x = 17, or, \[\frac{2x}{2}=\frac{17}{2}\], or, \[x=\frac{17}{2}\]
(a) 7 (b) 21
(c) \[\frac{7}{2}\] (d) 14
(e) None of these
Answer: (d)
Explanation: Let be the number is x.
Now, four times of the number = 4x
According to question, \[4x=56\], or,\[\frac{4x}{4}=\frac{56}{4},\,\,or,\,\,x=14\]
3(2m – 1) + 4 = 16
(a)\[\frac{5}{4}\] (b) \[\frac{5}{2}\]
(c) 5 (d) \[\frac{1}{5}\]
(e) None of these
Answer: (b)
Explanation: 3(2m – 1) + 4 = 16, or, 3(2m –1) + 4 – 4 = 16 – 4
Or, 3(2m – 1) = 12, or, \[\frac{3\left( 2m-1 \right)}{3}=\frac{12}{3}\]
Or, 2m – 1 = 4, or, 2m – 1 + 1 = 4 + 1, or 2m = 5
Or, \[\frac{2m}{2}=\frac{5}{2},\,\,or\,\,m=\frac{5}{2}\]
(a) 31 (b) 27
(c) 32 (d) 33
(e) None of these
Answer: (d)
Explanation: Given that x = 2 and y = 5.
Now, \[{{x}^{\mathbf{3}}}+{{y}^{\mathbf{2}}}=\left( x \right)~\times \left( x \right)~\times \left( x \right)+\left( y \right)~\times \left( y \right)=(2~\times 2~\times 2)+(5~\times 5)=8+25=33\].
(a) 3a (b) 3b
(c) 3ab (d) \[3{{a}^{2}}b\]
(e) None of these
Answer: (c)
Explanation: \[\frac{15{{a}^{2}}b}{5a}=\frac{15\times {{a}^{2}}\times b}{5\times a}=\frac{3\times \times \times a\times b}{\times }=\frac{3\times a\times b}{1}=3ab\]
(a) 3 (b) 4
(c) 1 (d) 8
(e) None of these
Answer: (b)
Explanation: Given equation is \[3{{x}^{2}}+4x+1\]
Coefficient of \[{{x}^{2}}\] is 3 and Coefficient of x is 4, Constant is 1.
You need to login to perform this action.
You will be redirected in
3 sec
