Types of Numbers
Category : 6th Class
![]() Natural
Natural
Numbers Every counting number is called natural numbers. Zero is excluded from the natural numbers because it does not represent the number of counted objects.
1, 2, 3, 4, 5, etc. are natural numbers.
Therefore, the numbers that are used in counting are called natural numbers.
Highest natural number is infinite or cannot be defined but lowest natural number is 1.
Natural numbers are represented by N (First capital letter of its name).
![]()
Find the first five natural numbers from the following sets of numbers:
(a) 2, 3, 5, 7, 8
(b) 1, 2, 3, 4, 5
(c) 10, 11, 12, 13, 14
(d) None of these
(e) All of these
Answer: (b)
Explanation
1, 2, 3, 4, 5 are the first five natural numbers.
![]() Whole Numbers
Whole Numbers
When 0 is included with counting numbers, it becomes whole number. Whole number is represented by W (First letter of its name). Whole numbers (W) = {0, 1, 2, 3, 4 ...infinite}.
Highest whole number cannot be defined but lowest is 0.
All natural numbers are whole number but all whole numbers are not natural numbers.
![]()
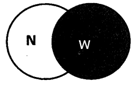
If N is the set of all natural numbers and W is the set of all whole numbers then overlapped part of N represent of which one of the following numbers?
(a) 1
(b) 0
(c) 2
(d) All of these
(e) None of these
Answer: (b)
Explanation
Zero is not the member of the set of natural numbers. Hence, overlapped part of N represent zero.
![]() Prime Numbers
Prime Numbers
The numbers which have only two factors, 1 and the number itself are called prime numbers. The following numbers 2, 3, 5,7,11,13,17,19, 23 do not have factor other than 1 and the number itself, therefore, they are called prime numbers.
![]()
Consider the following statements:
Statement 1: The set of all natural numbers is prime number.
Statement 2: The set of numbers which does not have factor other than 1 and the number itself is called prime number.
Which one of the following options is correct?
(a) Statement 1 is true and 2 is false
(b) Statement 1 is false and 2 is true
(c) Both the statements are false
(d) None of these
(e) All of these
Answer:(b)
Explanation
Every natural number is not prime number and the number which has only two factors 1 and the number itself is called prime number.
![]() Composite Numbers
Composite Numbers
The numbers which have more than two factors are called composite numbers. The factors of the following number, 4, 6 and 10 are:
Factors of 4 = 1, 2, 4 (Three factors) Factors of 6 = 1, 3, 6 (Three factors)
Factors of 10 = 1, 2, 5, 10 (Four factors). Therefore, the numbers 4, 6 and 10 are composite numbers, whereas the factors of 11, 13, and 17 are:
Factors of 11 are 1 and 11. Factors of 13 are 1 and 13 and factors of 17 are 1 and17, therefore, the numbers 11, 13 and 17 are not the composite numbers. Note: Except 2 all the even numbers are composite numbers.
![]()
If a number is divided by 2 leaves no remainder then the number is:
(a) Even number
(b) Odd Numbers
(c) Prime numbers
(d) None of these
(e) All of these
Answer: (a)
Explanation
Every even number is exactly divisible by 2.
![]() Co-Prime
Co-Prime
Two numbers whose H.C.F. (Highest Common Factor) is 1 are called Co - Prime. HCF of 2 and 3 is 1 therefore, pair of 2 and 3 is called co - prime. HCF of 3 and 9 is3, therefore, 3 and 9 is not a co - prime.
![]()
From the following sets of numbers, which one is the set of co-primes?
(a) {8,16}
(b) {10,100}
(c) {3,5}
(d) All of these
(e) None of these
Answer: (c)
Explanation
Positive common factor of 3 and 5 is not other than 1,therefore, called co prime.
![]() Rational and Irrational numbers
Rational and Irrational numbers
The number in the form of \[\frac{p}{q}\] where \[p\ne 0\] and p, q are integers is called rational number. Therefore, rational numbers are always in ratio form. Integer 6 can also be represented in the form of \[\frac{6}{1}\] hence, 6 is also a rational number. The decimal number which decimal part is neither terminating nor repeating is called irrational number, i.e. Decimal form of\[\sqrt{2}=1.4142134623.\]The decimal part of \[\sqrt{2}\]is non-terminating non-repeating. Hence, \[\sqrt{2}\] is an irrational number.
![]()
Simplify the following: \[\sqrt{\frac{1}{2}+\frac{5}{2}}\] and find the solution is a rational or irrational number.
(a) Irrational number
(b) Rational number
(c) Solution is zero
(d) All of these
(e) None of these
Answer: (a)
Explanation
\[\sqrt{\frac{1}{2}+\frac{5}{2}}=\sqrt{\frac{6}{2}=}\sqrt{3},\]which is an irrational number.
![]() Successor
Successor
Successor of every number comes just after the number. Therefore, the successor of every number is obtained by adding 1 to the number. Successor of 25 = 25 + 1 = 26 but 25 - 1 = 24 is not the successor of 25.
![]()
Consider the following two statements:
Statement 1: Successor of every number is obtained by multiplying 1 to the number.
Statement 2: Successor of every number is obtained by adding 1 to the number.
Which one of the following options is correct?
(a) Statement 1 is false and 2 is true
(b) Statement 1 is true and 2 is false
(c) Both statements are false
(d) All of these
(e) None of these
Answer: (a)
![]() Predecessor
Predecessor
Predecessor of every number comes just before the number. Predecessor of 23 is obtained by subtracting 1 from the number therefore, the predecessor of 23 = 23 - 1=22.
![]()
A set of numbers is {45, 67, 89}. Which one of the following is the predecessor of the given set of numbers?
(a) {44,68,90}
(b) {44,66,88}
(c) {46,68,90}
(d) All of these
(e) None of these
Answer: (b)
Explanation
Predecessor of given set of numbers is {44, 66, 88}
You need to login to perform this action.
You will be redirected in
3 sec
